2006年辽宁省十一市中等学校招生考试(课改实验区)
考试时间120分钟,试卷满分150分
一、选择题(下列各题的备选答案中,只有一个是正确的,请将正确答案的序号填入下表中相应题号下的空格内.每小题3分,共24分)
1.据2006年5月27日《沈阳日报》报道,“五 一”黄金周期间2006年沈阳“世园会”的游客接待量累计1760000人次.用科学记数法表示为( )
一”黄金周期间2006年沈阳“世园会”的游客接待量累计1760000人次.用科学记数法表示为( )
A. 人次 B.
人次 B.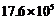 人次
人次
C.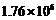 人次 D.
人次 D.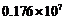 人次
人次
2.一辆汽车由 地匀速驶往相距300千米的
地匀速驶往相距300千米的 地,汽车的速度是100千米/小时,那么汽车距离
地,汽车的速度是100千米/小时,那么汽车距离 地的路程
地的路程 (千米)与行驶时间
(千米)与行驶时间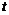 (小时)的函数关系用图象表示为( )
(小时)的函数关系用图象表示为( )
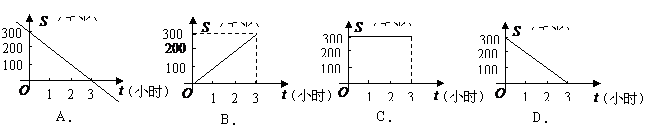
3.一鞋店试销一种新款女鞋,一周内各种型号的鞋卖出的情况如下表所示:
型号
22
22.5
23
23.5
24
24.5
25
数量(双))
3
5
10
15
8
4
2
对这个鞋店的经理来说,他最关注的是数据的( )
A.平均数 B.众数 C.中位数 D.极差
4.一个三角形的两边长为3和6,第三边的边长是方程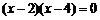 的根,则这个三角形的周长是( )
的根,则这个三角形的周长是( )
A.11 B.11或13 C.13 D.11和13
5.李明设计了下面四种正多边形的瓷砖图案,用同一种瓷砖可以平面密铺的是( )
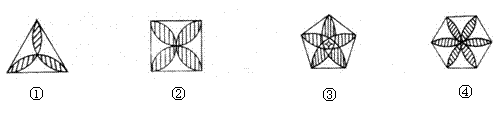 |
A.①②④ B.②③④ C.①③④ D.①②③
6.在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有4个红球且摸到红球的概率为 ,那么口袋中球的总数为( )
,那么口袋中球的总数为( )
A.12个 B.9个 C.6个 D.3个
7.小刚学习了有理数运算法则后,编了一个计算程序.当他输入任意一个有理数时,显示屏上出现的结果总等于所输入的有理数的平方与1的和.当他第一次输入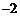 ,然后又将所得的结果再次输入后,显示屏上出现的结果应是( )
,然后又将所得的结果再次输入后,显示屏上出现的结果应是( )
A.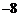 B.
B. C.
C. D.
D.
8.将一个正方形纸片依次按图(1),图(2)方式对折,然后沿图(3)中的虚线裁剪,最后将图(4)的纸再展开铺平,所看到的图案是( )
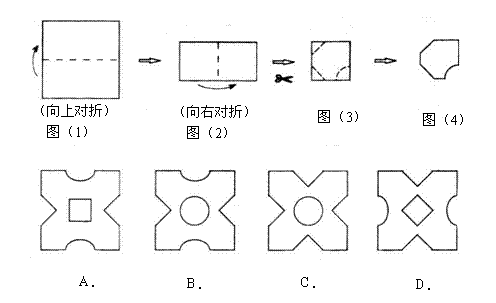 |
 二、填空题(每小题3分,共24分)
二、填空题(每小题3分,共24分)
9. 的相反数是 .
的相反数是 .
10.函数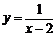 中,自变量
中,自变量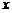 的取值范围是 .
的取值范围是 .

 11.右图中阴影部分是一个正方体的表面展开平面图形的一部分,请你在方格纸中补全这个正方体的表面展开平面图.(只填一种情形即可)
11.右图中阴影部分是一个正方体的表面展开平面图形的一部分,请你在方格纸中补全这个正方体的表面展开平面图.(只填一种情形即可)
12.如图, 是
是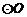 上三点,
上三点,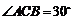 ,
,
则 的度数是 .
的度数是 .
13.不等式组 的解集为 .
的解集为 .
 14.已知二次函数
14.已知二次函数 ,其中
,其中
 满足
满足 和
和 ,则该
,则该
二次函数图象的对称轴是直线 .
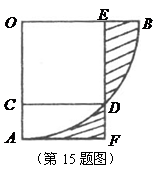
15.如图,扇形 的圆心角为
的圆心角为 ,四边形
,四边形
是边长为1的正方形,点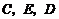 分别在
分别在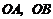 ,
,
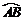 上,过
上,过 作
作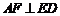 交
交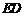 的延长线于点
的延长线于点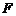 ,那
,那
 么图中阴影部分的面积为 .
么图中阴影部分的面积为 .
16.如图,有一种动画程序,屏幕上正方形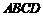 是黑色区域(含正方形边界),其中
是黑色区域(含正方形边界),其中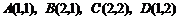 ,用信号枪沿直线
,用信号枪沿直线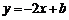 发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的
发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的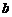 的取值范围为 .
的取值范围为 .
三、(每题8分,共16分)
17.先化简,再求值: ,其中
,其中 ,
,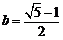 .
.
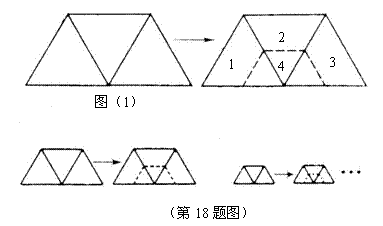 18.如图,用三个边长为
18.如图,用三个边长为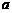 的等边三角形拼成如图(1)所示的等腰梯形,现将这个等腰梯形截成四个全等的等腰梯形(图中的1,2,3,4部分).然后将其中的一个等腰梯形按照上述方法再截成四个全等的等腰梯形.如此重复下去
的等边三角形拼成如图(1)所示的等腰梯形,现将这个等腰梯形截成四个全等的等腰梯形(图中的1,2,3,4部分).然后将其中的一个等腰梯形按照上述方法再截成四个全等的等腰梯形.如此重复下去 .求第
.求第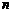 次截得的一个等腰梯形的周长和面积.
次截得的一个等腰梯形的周长和面积.
四、(每题10分,共20分)
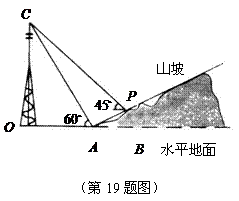 19.如图,某人在山坡坡脚
19.如图,某人在山坡坡脚 处测得电视塔尖点
处测得电视塔尖点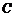 的仰角为
的仰角为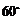 ,沿山坡向上走到
,沿山坡向上走到 处再测得点
处再测得点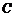 的仰角为
的仰角为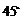 ,已知
,已知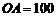 米,山坡坡度为
米,山坡坡度为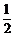 (即
(即 )且
)且 在同一条直线上.求电视塔
在同一条直线上.求电视塔 的高度以及此人所在位置点
的高度以及此人所在位置点 的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
20.某网站公布了某城市一项针对2006年第一季度购房消费需求的随机抽样调查结果,下面是根据调查结果制作的购房群体可接受价位情况的比例条形统计图和扇形统计图的一部分.
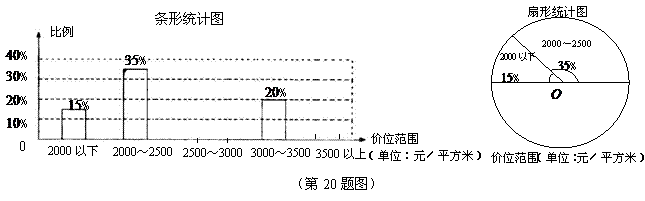
请根据统计图中提供的信息回答下列问题:
(1)若2500~3000可接受价位所占比例是3500以上可接受价位所占比例的5倍,则这两个可接受价位所占的百分比分别为 .
(2)补全条形统计图和扇形统计图;
(3)购房群体中所占比例最大的人群可接受的价位是 ;
(4)如果2006年第一季度该市所有的有购房需求的人数为50000人,试估计这些有购房需求的人中可接受3500元/平方米以上的人数是 人.
五、(每题10分,共20分)
如图,已知 的面积为3,且
的面积为3,且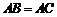 ,现将
,现将 沿
沿 方向平移
方向平移 长度得到
长度得到 .
.
(1)求 所扫过的图形的面积;
所扫过的图形的面积;
(2)试判断 与
与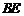 的位置关系,并说明理由;
的位置关系,并说明理由;
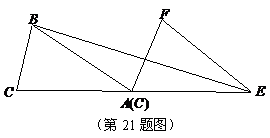 (3)若
(3)若 ,求
,求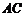 的长.
的长.
 |
 (1)用树状图或列表法,求两数相加和为零的概率;
(1)用树状图或列表法,求两数相加和为零的概率;
(2)你认为这个游戏规则对双方公平吗?若公平,请说明理由;若不公平,请修改游戏规则中的赋分标准,使游戏变得公平.
六、(每题10分,共20分)
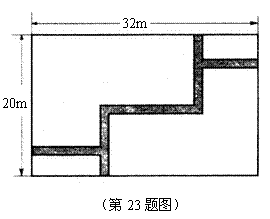 23.如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为
23.如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为 ,求道路的宽.(部分参考数据:
,求道路的宽.(部分参考数据: ,
,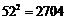 ,
, )
)
24.如图, 是
是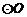 的直径,
的直径,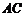 是弦,
是弦,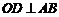 交
交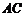 于点
于点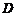 .若
.若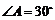 ,
, .求
.求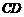 的长.
的长.
 |
七、(12分)
25.北方某水果商店从南方购进一种水果,其进货成本是每吨0.4万元,根据市场调查这种水果在北方市场上的销售量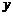 (吨)与每吨的销售价
(吨)与每吨的销售价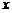 (万元)之间的函数关系如下图所示:
(万元)之间的函数关系如下图所示:
(1)求出销售量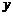 与每吨销售价
与每吨销售价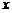 之间的函数关系式;
之间的函数关系式;
(2)如果销售利润为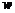 (万元),请写出
(万元),请写出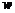 与
与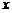 之间的函数关系式;
之间的函数关系式;
(3)当每吨销售价为多少万元时,销售利润最大?最大利润是多少?
 |
八、(14分)
26.如图,四边形 是一张放在平面直角坐标系中的正方形纸片.点
是一张放在平面直角坐标系中的正方形纸片.点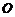 与坐标原点重合,点
与坐标原点重合,点 在
在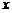 轴上,点
轴上,点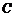 在
在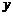 轴上,
轴上, ,点
,点 为
为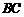 的中点,点
的中点,点 的坐标为
的坐标为 ,过点
,过点 且平行于
且平行于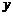 轴的直线
轴的直线 与
与 交于点
交于点 .现将纸片折叠,使顶点
.现将纸片折叠,使顶点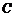 落在
落在 上,并与
上,并与 上的点
上的点 重合,折痕为
重合,折痕为 ,点
,点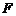 为折痕与
为折痕与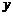 轴的交点.
轴的交点.
(1)求点 的坐标;
的坐标;
(2)求折痕 所在直线的解析式;
所在直线的解析式;
(3)设点 为直线
为直线 上的点,是否存在这样的点
上的点,是否存在这样的点 ,使得以
,使得以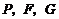 为顶点的三角形为等腰三角形,若存在,请直接写出点
为顶点的三角形为等腰三角形,若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 |