2006年山东济宁市中等学校招生考试(课标卷)
第Ⅰ卷
一、选择题(每小题3分,共36分,下列各题只有一个正确选项)
1. 的相反数是( )
的相反数是( )
A.  B.
B.  D.
D. 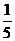
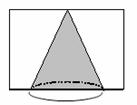
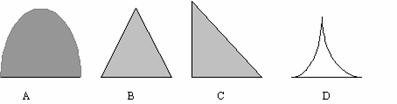
2.如图,一平面经过圆锥的顶点截圆锥所得到的截面形状是( )
3.若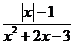 的值为零,则x的值是( )
的值为零,则x的值是( )
A.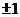 B.
B. D.不存在
D.不存在
4.如图,将一等边三角形剪去一个角后,∠1+∠2等于( )
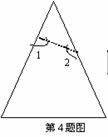
A.120° B.240° C.300° D.360°
5.下列图形中,不能用同一种作平面镶嵌的是( )
A.正三角形 B. 正方形 C.正五边形 D.正六边形
6.  能被下列数整除的是( )
能被下列数整除的是( )
A. 3 B.
7.王强从A处沿北偏东60°的方向到达B处,又从B处沿南偏西25°的方向到达C处,则王强两次行进路线的夹角为( )
A.145° B. 95° C. 85° D.35°
8.二次函数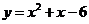 的图像与x轴交点的横坐标是( )
的图像与x轴交点的横坐标是( )
A.2和-3 B.-2和
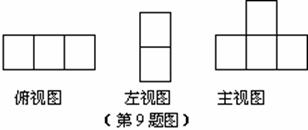
9.如图是由一些相同的小正方形构成的几何体的三视图,那么构成这个几何体的小正方体的个数为( )
A.7个 B.6个 C.5个 D.4个
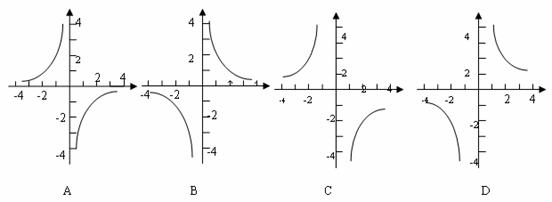
10.反比例函数 与正比例函数
与正比例函数 图像的一个交点的横坐标为1,则反比例函数的图像大致为( )
图像的一个交点的横坐标为1,则反比例函数的图像大致为( )
11.如图,将点A1(6,1)向左平移4个单位到达点A2的位置,再向上平移3个单位到达点A3的位置,△A
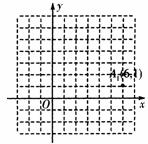
A.(-2,1) B.(1,1) C.(-1,1) D.(5,1)
12.如图,以BC为直径,在半径为2圆心角为900的扇形内作半圆,交弦AB于点D,连接CD,则阴影部分的面积是( )
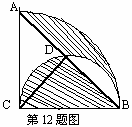
A.π-1 B.π- D.
D. 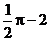
第Ⅱ卷、
二、填空题(每小题3分,共18分,只要求填写最后结果)
13.炭氢化合物的化学式为:CH4、C2H5、C3H8、C4H10,……,观察其化学式的变化规律,则第n个炭氢化合物的化学式为_____________。
14.如下左图是济宁日报


15.如上右图,已知李明的身高为
16.甲、乙两同学手中各有分别标注1,2,3三个数字的纸牌,甲制定了游戏规则:两人同时各出一张牌,当两纸牌上的数字之和为偶数时甲赢,奇数时乙赢。你认为此规则公平吗?并说明理由。____________________________________
17.如图,△ABC中,AB=AC,∠A=45°,AC的垂直平分线分别交AB,AC于D,E两点,连接CD。如果AD=1,那么tan∠BCD=__________。
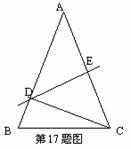
18.某市出租车收费标准:乘车不超过2公里收费5元,多于2公里不超过4公里,每公里收费1.5元,4公里以上每公里收费2元。张舒从住处乘坐出租车去车站送同学,到车站时计费表显示7.25元。张舒立即沿原路返回住处,那么他乘坐原车和换乘另外出租车相比,哪种方法省钱?___________省多少?_________
三、解答题(共66分,解答应写出文字说明、证明过程或推演步骤)
19.(8分)解下列不等式组,并在数轴上表示出该不等式组的解集。
20.(8分)
鞋子的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组“鞋码”与鞋长的对应数值:
鞋长
16
19
24
27
鞋码
22
28
38
44
(1)分析上表,“鞋码”与鞋长之间的关系符合你学过的那种函数?
(2)设鞋长为x,“鞋码”为y,求y与x之间的函数关系式;
(3)如果你需要的鞋长为
21.(9分)
某农机公司为更好地服务于麦收工作,按图1给出的比例,从甲、乙、丙三个工厂共购买了150台同种农机,公司技术人员对购买的这批农机全部进行了检验,绘制了如图2所示的统计图。
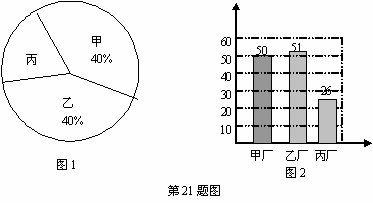
请你根据图中提供的信息,解答一下问题:
(1)求该农机公司从丙厂购买农机的台数;
(2)求该农机公司购买的150台农机中优等品的台数;
(3)如果购买的这批产品质量能代表各厂的产品质量状况,那么:
① 从优等品的角度考虑,哪个工厂的产品质量较好些?为什么?
② 甲厂2005年生产的360台产品中的优等品有多少台?
22.(9分)
如图,在△ABC中,∠C=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N。
(1)求证:BA?BM=BC?BN;
(2)如果CM是⊙O的切线,N为OC的中点。当AC=3时,求AB的值。

23.(10分)
直角三角形通过剪切可以拼成一个与该直角三角形面积相等的矩形。方法如下:

请你用上面图示的方法,解答下列问题:
(1)对任意三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形面积相等的矩形。
(2)对任意四边形,设计一种方案,将它分成若干块,再拼成一个与原四边形面积相等的矩形。
24.(10分)
随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场。一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售。预计每箱水果的盈利情况如下表:
A种水果/箱
B种水果/箱
甲店
11元
17元
乙店
9元
13元
有两种配货方案(整箱配货):
方案一:甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱;
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店_________箱,乙店__________箱;B种水果甲店_________箱,乙店__________箱。
(1)如果按照方案一配货,请你计算出经销商能盈利多少元?
(2)请你将方案二填写完整(只填写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多?
(3)在甲、乙两店各配货10箱,且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
25.(12分)
如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B。P为线段AB上一动点,作直线PC⊥PO,交直线x=1于点C。过P点作直线MN平行于x轴,交y轴于点M,交直线x=1于点N。
(1)当点C在第一象限时,求证:△OPM∽△PCN;
(2)当点C在第一象限时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线x=1上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰直角三角形的点P的坐标;如果不可能,请说明理由。