2005年海南省中等学校招生
第一卷
一、选择题:(本大题满分36分,每小题3分。在下列各题的四个备选答案中,只有一个是正确的)
1.如果零上3℃记作+3℃,那么零下3℃记作( )
A.?3 B.?6 C.?3℃ D.?6℃
2.下列各点中,在第一象限的点是( )
A.(2,3) B.(2,?3) C.(?2,3) D.(?2,?3)
3.海南的富铁矿是国内少有的富铁矿之一,储量居全国第6位,其储量约为237000000吨,用科学记数法表示应为( )
A.237×106吨 B.2.37×107吨 C.2.37×108吨 D.0.237×109吨
4.一次函数y=2x+1的图像经过( )
A.第二、三、四象限 B.第一、三、四象限
C.第一、二、四象限 D.第一、二、三象限
5.不等式组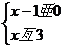 的解集是( )
的解集是( )
A.x>1 B.1<x<3 C.x>?1 D.x<3
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
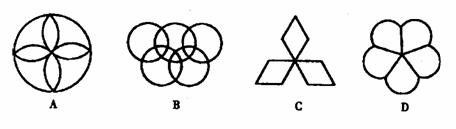
7.方程x2+3x+1=0的根的情况是( )
A.没有实数根 B.有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
8.化简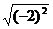 的结果是( )
的结果是( )
A.?2 B.土2 C.2 D.4
9.已知一个正六边形的半径是r,则此正六边形的周长是( )
A.3r B.6r C.12r D.24r
10.在△ABC中,∠C=90º,BC=3,AB=5,则sinA的值是( )
A.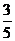 B.
B.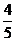 C.
C.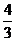 D.
D.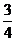
11.如图,在△ABC中,∠A=36º,∠C=72º,∠ABC的平分线交AC于D,则图中共有等腰三角形( )
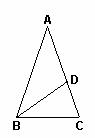 11题图
11题图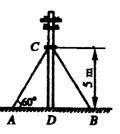 12题图
12题图
A.0个 B.1个 C.2个 D.3个
12.如图,要在离地面5m处引拉线固定电线杆,使拉线和地面成60º角,若考虑既要符合设计要求,又要节省材料,则在库存的l1=5.2m、l2=6.2m、l3=7.8m、l4=10m四种备用拉线材料中,拉线AC最好选用( )
A.l1 B.l2 C.l3 D.l4
第二卷
二、填空题:(本大题满分24分,每小题3分)
13.9的算术平方根是____平方根___。
14.分解因式:x3?4x=_______因式分解____________。
15.计算: =____二次根式的化简_______。
=____二次根式的化简_______。
16.如图A、B、C、D在同一直线上,AB=CD,DE∥AF,若要使△ACF≌△DBE,则还需要补充一个条件:_____全等三角形________。

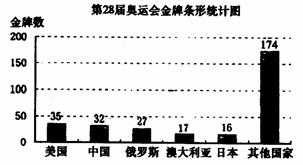
17.在2004年的第28届奥运会上,中国体育代表团取得了很好的成绩。由金牌条形统计图(如图)提供的信息可知,中国代表团的金牌总数约占奥运会金牌总数的__统计__%(结果保留两个有效数字)。
18.在比例尺为1∶2700000的海南地图上量得海口与三亚间距离约8厘米,则海口与三亚两城间的实际距离约是__比例线段_________千米。
19.已知反比例函数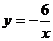 的图像经过点P(2,a),则a=__反比例函数的性质____。
的图像经过点P(2,a),则a=__反比例函数的性质____。
20.如图,AB是⊙O的直径,C是BA延长线上一点,CD切⊙O 于点D,CD=4,CA=2,则⊙O的半径为____圆_____。

三、解答下列各题:(本大题满分90分,其中21至24题各10分,25、26题各11分,27、28题各14分)
21.已知: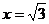 ,y=?1,求x2+2y2?xy的值。
,y=?1,求x2+2y2?xy的值。
22.解方程:
23、下面是某种细胞分裂示意图(如图),这种细胞每过30分钟便由1个分裂成2个。
根据此规律可得:
(1)这样的一个细胞经过第四个30分钟后可分裂成____个细胞;
(2)这样的一个细胞经过3小时后可分裂成____个细胞;
(3)这样的一个细胞经过n(n为正整数)小时后可分裂成______个细胞。
24.在当地农业技术部门指导下,小明家增加种植菠萝的投资,使今年的菠萝喜获丰收。下面是小明爸爸、妈妈的一段对话。

请称用学过的知识帮助小明算出他们家今年菠萝的收入。(收入―投资=净赚)
25.如图,在等腰梯形ABCD中,AD∥BC,∠C=60º,AD=10,AB=18,求BC的长.(画出图形,再解答。)
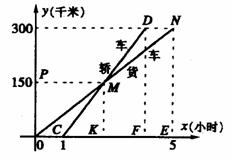
26.在我省环岛高速公路上,一辆轿车和一辆货车沿相同路线从A地到B地,所经过的路程y(千米)与时间x(小时)的函数关系图像如图所示,试根据图像,回答下列问题:
(1)货车比轿车早出发________小时,轿车追上货车时行驶了________千米。A地到B地的距离为________千米。
(2)轿车追上货车需多少时间?
(3)轿车比货车早到多少时间?
27.如图,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连结DE交BG的延长线于H .
(1)求证:①△BCG≌△DCE;②BH⊥DE。
(2)试问当点G运动到什么位置时,BH垂直平分DE?请说明理由。

28.如图,在平面直角坐标系中,过坐标原点O的⊙M分别交x轴、y轴于点A(6,0)、
B(0,?8).
(1)求直线AB的解析式;
(2)若有一条抛物线的对称轴平行于y轴且经过M点,顶点C在⊙M上,开口向下,且经过点B,求此抛物线的解析式;
(3)设(2)中的抛物线与x轴交于D(x1,y1)、E(x2,y2)两点,且x1<x2,在抛物线上是否存在点P,使△PDE的面积是△ABC面积的 ?若存在,求出P点的坐标,若不存在,请说明理由.
?若存在,求出P点的坐标,若不存在,请说明理由.