2005年淄博市中等学校招生考试
第I卷
一、选择题:本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项涂在答题卡的相应位置上.第1-6小题每题3分,第7-12小题每题4分.错选、不选或选出的答案超过一个,均记零分.
1.下列计算正确的是合并同类项.
(A)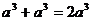 (B)
(B)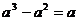
(C)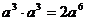 (D)
(D)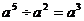
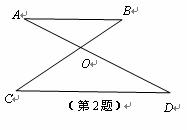
2.如图, AB//CD,AD,BC相交于点O,∠BAD=35°,∠BOD=76°,则∠C的度数是平行线的性质.
(A)∠31° (B)∠35°
(C)∠41° (D)∠76°
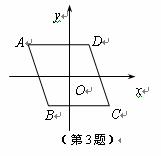
3.如图,菱形ABCD的中心在直角坐标系的原点上,且AD//x轴,点A的坐标为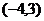 ,那么点C的坐标为
,那么点C的坐标为
(A) (B)
(B)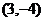
(C)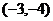 (D)
(D)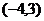
4.若点 ,
,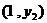 ,
,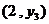 都在反比例函数
都在反比例函数 的图象上,则有
的图象上,则有
(A) (B)
(B)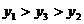
(C) (D)
(D)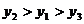
5.如图,数轴上A,B两点分别表示实数1,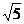 ,点B关于点A的对称点为C,则点C所表示的实数为
,点B关于点A的对称点为C,则点C所表示的实数为
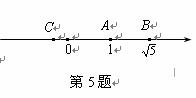
(A)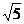 -2 (B)2-
-2 (B)2-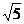 (C)
(C)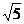 -3
(D)3-
-3
(D)3-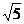
6.两个不相等的实数m,n满足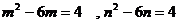 ,则mn的值为
,则mn的值为
(A)6
(B) (C)4
(D)
(C)4
(D)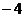
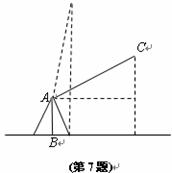
7.如图,一台起重机的机身AB高20米,吊杆AC的长为36米,吊杆对水平线的倾角可以从30°转到80°.则这台起重机工作时,吊杆端点C离地的最大高度和离机身AB的最远水平距离分别为
(A) 56米和 米
(B)38米和
米
(B)38米和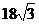 米
米
(C)36sin80°米和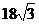 米
(D)(36sin80°+20)米和
米
(D)(36sin80°+20)米和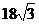
8. 不等式组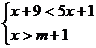 的解集是x>2,则m的取值范围是
的解集是x>2,则m的取值范围是
(A)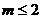 (B)
(B) (C)
(C) (D)
(D)
9.
如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与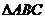 相似的是相似三角形的判定. 勾股定理
相似的是相似三角形的判定. 勾股定理


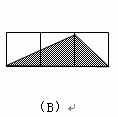


10. 学校计划将120名学生平均分成若干读书小组,若每小组比原计划多1人,则要比原计划少分出6个小组,那么原计划要分成的小组数是
(A)40 (B)30 (C)24 (D)20
11.如图,圆锥的母线长是3,底面半径是1,A是底面圆周上一点,从点A出发绕侧面一周,再回到点A的最短路线长是
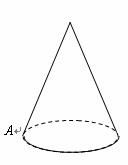
(A)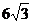 (B)
(B)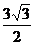
(C)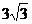 (D)
(D)
12.一水池有2个进水口,1个出水口,每个进水口进水量与时间的关系如图甲所示,出水口出水量与时间的关系如图乙所示.某天0点到6点,该水池的蓄水量与时间的关系如图丙所示.
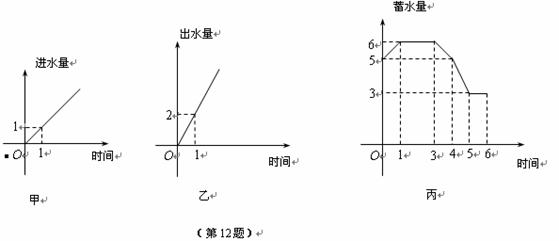
下面的论断中:①0点到1点,打开两个进水口,关闭出水口;②1点到3点,同时关闭两个进水口和一个出水口;③3点到4点,关闭两个进水口,打开出水口;④5点到6点,同时打开两个进水口和一个出水口.可能正确的是
(A) ①③ (B) ①④ (C) ②③ (D) ②④
第II卷
二、填空题:本题共5小题,满分20分.只要求填写最后结果,每小题填对得4分.
13.台湾是我国最大的岛屿,总面积为35989.76平方千米,这个数据用科学记数法表示为 平方千米(保留两个有效数字)
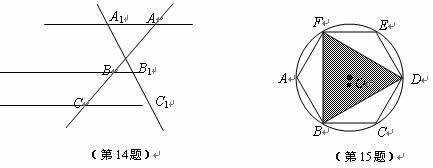
14.如图,直线A1A//BB1//CC1,若AB=8,BC=4,A1B1=6则线段B1C1的长是 .
15.已知正六边形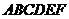 内接于⊙O,图中阴影部分的面积为
内接于⊙O,图中阴影部分的面积为 ,则⊙O的半径为
.
,则⊙O的半径为
.
16.已知抛物线 经过点
经过点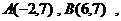
 ,则该抛物线上纵坐标为
,则该抛物线上纵坐标为 的另一点的坐标是
的另一点的坐标是
17.在平面直角坐标系中,横坐标、纵坐标都是整数的点称为整点.观察图中每一个正方形(实线)四条边上的整点的个数,请你猜测由里向外第10个正方形(实线)四条边上的整点
共有 个.

三、解答题:本题共7小题,共58分.解答应写出文字说明、证明过程或演算步骤 .
18.(本题满分5分)
已知 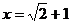 ,求
,求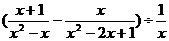 的值.
的值.
19.(本题满分7分)
时代中学初二年级准备从部分同学中挑选出身高差不多的40名同学参加校广播体操比赛,这部分同学的身高(单位:厘米)数据整理之后得到下表
身高x(厘米)
频数
频率

6
0.1
155 158
158
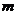
0.2
158 161
161
18

161 164
164
11
164 167
167
8
167 170
170
3
170 173
173
2
合计
(1)表中m , n ;
(2)身高的中位数落在哪个范围内?请说明理由;
(3)应选择身高在哪个范围内的学生参加比赛?为什么?
20.(本题满分8分)
如图,⊙O1和⊙O2外切于点P,直线AB是两圆的外共切线,A,B为切点,试判断以线段AB为直径的圆与直线O1O2的位置关系,并给出证明.
21.(本题满分8分)
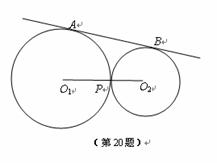
如图,一副三角尺叠放在一起,含45°角的三角尺的斜边与含30°角的三角尺的长直角边恰好重合.
(1)求∠AEB的度数
(2)若含30°角的三角尺的短直角边BD长为a求两三角尺重叠部分△ABE的面积.
22.(本题满分10分)
某水果批发市场香蕉的价格如下表:
购买香蕉数
不超过20千克
20千克以上
但不超过40千克
40千克以上
每千克价格
6元
5元
4元
张强两次共购买香蕉50千克(第二次多于第一次),共付出264元,请问张强第一次、第二次分别购买香蕉多少千克?
23.(本题满分10分)
如图,四边形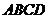 是等腰梯形,
是等腰梯形,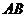 ∥
∥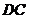 .由4个这样的等腰梯形可以拼出图乙所示的平行四边形.
.由4个这样的等腰梯形可以拼出图乙所示的平行四边形.
(1)求四边形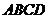 四个内角的度数;
四个内角的度数;
(2)试探究四边形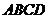 四条边之间存在的等量关系,并说明理由;
四条边之间存在的等量关系,并说明理由;
(3)现有图甲中的等腰梯形若干个,利用它们你能拼出一个菱形吗?若能,请你画出大致的示意图.

24.(本题满分10分)
如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与A,D不重合).BE的垂直平分线交AB于点M, 交DC于点N
(1)设AE=x,四边形ADNM的面积为S.写出S关于x的函数关系式;
(2)当AE为何值时,四边形ADNM的面积最大?最大值是多少?
