2005年嘉定区九年级数学学业考试模拟试卷
一、填空题(本题共14题,每题3分,满分42分)
1、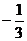 的倒数是
.
的倒数是
.
2、用科学记数法表示: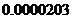 =
.
=
.
3、分解因式: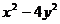 =
.
=
.
4、不等式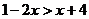 的解集为
.
的解集为
.
5、若关于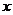 的方程
的方程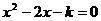 有两个不相等的实数根,则
有两个不相等的实数根,则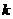 的取值范围为 .
的取值范围为 .
6、函数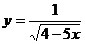 的定义域是
.
的定义域是
.
7、反比例函数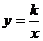 的图象经过点(
的图象经过点(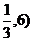 ,则
,则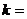 .
.
8、将抛物线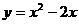 向右平移2个单位后,所得抛物线的顶点坐标为
.
向右平移2个单位后,所得抛物线的顶点坐标为
.
9、若长度分别为4、6、x的三条线段能组成一个三角形,则x的取值范围是 .
 10、若梯形的中位线长为5,面积为20,则这个梯形的高为 .
10、若梯形的中位线长为5,面积为20,则这个梯形的高为 .
11、在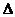 ABC中,AB=AC=6,BC=4,则cos
ABC中,AB=AC=6,BC=4,则cos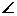 C= .
C= .
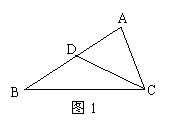
12、如图1:已知在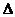 ABC中,点D在边AB上,
ABC中,点D在边AB上,
AD=4,BD=5,AC=6,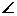 B=28
B=28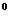 ,
,
则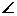 ACD= .
ACD= .
13、在矩形ABCD中,AB=5,BC=12,对角线AC与BD相交于点O,以点O为圆心,6.5
为半径的圆与直线AB的位置关系是 .
14、在Rt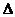 ABC中,
ABC中,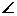 C=90
C=90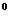 ,AC=8,BC=6,
,AC=8,BC=6,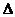 ABC绕点B逆时针旋转,当点C恰好落在斜边AB上时,点A落在 A
ABC绕点B逆时针旋转,当点C恰好落在斜边AB上时,点A落在 A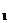 点,连结AA
点,连结AA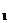 ,则AA
,则AA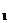 = .
= .
[本大题每题列出的四个答案中,只有一个是正确的,把正确的答案的代号填入括号内]
二、选择题(本题共4题,每题3分,满分12分)
15、下列各数中是有理数的是 ( )
(A)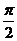 (B)
(B)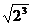 (C)
(C)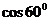 (D)
(D)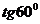
16、下列二次根式中,属最简二次根式的是 ( )
(A) (B)
(B)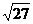 (C)
(C)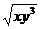 (D)
(D)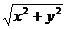
17、若关于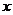 的方程
的方程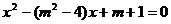 的两个实数根分别为
的两个实数根分别为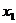 、
、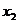 ,且
,且
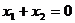 ,则
,则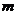 的值为
( )
的值为
( )
(A)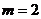 (B)
(B)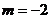 (C)
(C)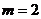 或
或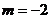 (D)
(D)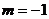
18、下列四个命题中,正确的命题是
(A)一组对边平行的四边形是梯形 (B)面积相等的两个直角三角形全等
(C)只有一条公切线的两圆内切 (D)等边三角形是一个中心对称图形
三、(本大题共3题,每题8分,满分24分)
19、先化简,再求值: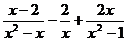 ,其中
,其中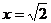 .
.
20、如图2:已知在Rt ABC中,
ABC中,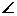 ACB=90
ACB=90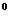 ,点D在边BC上,过点D作DE∥AC
,点D在边BC上,过点D作DE∥AC
交AB于点E,AB=10,AC=8,CD=4.
 求:(1)sinA的值;
求:(1)sinA的值;
(2)DE的长.
21、某电脑店共有6名员工,所有员工的每月工资情况如下表所示:
人员
经理
调试员1
调试员2
收银员
勤杂工
临时工
人数
1
1
1
1
1
1
工资
5000元
1200元
1000元
600元
550元
350元
根据上述提供的信息,回答下列问题:
(1)这个电脑店所有员工每月的平均工资为 元;
(2)如去掉经理、临时工的每月工资,其他员工每月的平均工资为 元;
(3)所有员工每月工资的中位数是 元;
(4)用平均数还是用中位数描述该电脑店员工每月工资的情况比较恰当?答: .
四、(本大题共4题,第22、23、24题每题10分,第25题12分,满分42分)
22、小杰带着10元钱去某文具商店购买铅笔,由于铅笔价格较高,就与该商店的营业员讨价还价,结果与营业员谈成每支铅笔降价0.25元,这样同样花10元钱,小杰比原来多买了2支铅笔。若该商店进这种铅笔时,每100支99.5元,问该商店在小杰身上赚了还是赔了?请说明理由.
23、如图3:已知O是菱形ABCD对角线BD上一点,以O为圆心,OD为半径的圆O
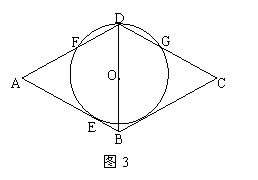 与AB相切于E点,与AD、CD分别相交于F、G点.
与AB相切于E点,与AD、CD分别相交于F、G点.
(1)求证:BC与圆O相切;
(2)若 A =60
A =60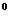 ,AB=2,求圆O的半径.
,AB=2,求圆O的半径.
24、如图4:一次函数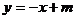 的图象与二次函数
的图象与二次函数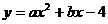 的图象交于
的图象交于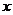 轴上一点A,且交
轴上一点A,且交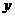 轴于点B,点A的坐标为
轴于点B,点A的坐标为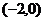 .
.
(1)求一次函数的解析式;
(2)设二次函数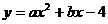 的对称轴为直线
的对称轴为直线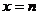 (
(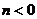 ),
),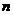 是
是
方程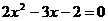 的一个根,求二次函数的解析式;
的一个根,求二次函数的解析式;
(3)在(2)条件下,设二次函数交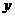 轴于点D,在
轴于点D,在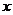 轴上有一点C,使以点A、B、C
轴上有一点C,使以点A、B、C
组成的三角形与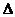 ADB相似.试求出C点的
ADB相似.试求出C点的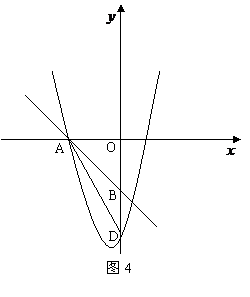 坐标.
坐标.
25、已知在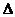 ABC中,
ABC中,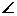 C=90
C=90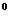 ,AC=BC=4,在射线AC、CB上分别有两动点M、N,且 AM=BN,连结MN交AB于点P.
,AC=BC=4,在射线AC、CB上分别有两动点M、N,且 AM=BN,连结MN交AB于点P.
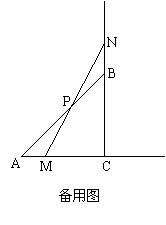
(1)如图5:当点M在边AC(与点A、C不重合)上,线段PM与线段PN之间有怎样的大小关系?试证明你得到的结论;
(2)当点M在射线AC上,若设AM=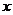 ,BP=
,BP=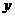 ,求
,求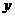 与
与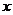 之间的函数关系式,并写出它的定义域;
之间的函数关系式,并写出它的定义域;
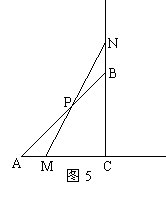
(3)过点M作直线AB的垂线,垂足为点Q,随着点M、N的移动,线段PQ的长能确定吗?若能确定,请求出PQ的长;若不能确定,请简要说明理由.
 |
|||
 |
|||