2006年上海市初中毕业生统一学业考试
(满分150分,考试时间100分钟)
一.填空题:(本大题共12题,满分36分)
 1.计算:
1.计算: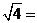 __________.
__________.
2.计算: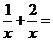 __________.
__________.
3.不等式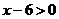 的解集是__________.
的解集是__________.
4.分解因式: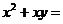 __________.
__________.
5.函数 的定义域是__________.
的定义域是__________.
6.方程 的根是__________.
的根是__________.
7.方程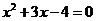 的两个实数根为
的两个实数根为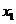 ,
,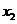 ,则
,则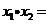 __________.
__________.
8.用换元法解方程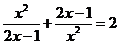 时,如果设
时,如果设 ,那么原方程可化为__________.
,那么原方程可化为__________.
9.某型号汽油的数量与相应金额的关系如图1所示,那么这种汽油的单价是每升______元.
10.已知在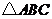 和
和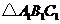 中,
中,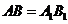 ,
,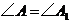 ,要使
,要使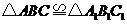 ,还需添加一个条件,这个条件可以是__________.
,还需添加一个条件,这个条件可以是__________.
11.已知圆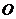 的半径为
的半径为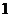 ,点
,点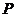 到圆心
到圆心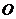 的距离为
的距离为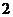 ,过点
,过点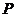 引圆
引圆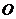 的切线,那么切线长是__________.
的切线,那么切线长是__________.
 12.在中国的园林建筑中,很多建筑图形具有对称性.图2是一个破损花窗的图形,请把它补画成中心对称图形.
12.在中国的园林建筑中,很多建筑图形具有对称性.图2是一个破损花窗的图形,请把它补画成中心对称图形.
【下列各题的四个结论中,有且只有一个结论是正确的,把正确结论的代号写在题后的圆括号内,选对得4分;不选、错选或者多选得零分】
二.选择题:(本大题共4题,满分16分)
13.在下列方程中,有实数根的是( )
A.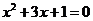 B.
B.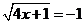
C.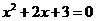 D.
D.
14.二次函数 图象的顶点坐标是( )
图象的顶点坐标是( )
A.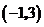 B.
B.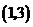 C.
C.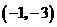 D.
D.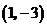
15.在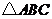 中,
中,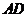 是
是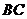 边上的中线,
边上的中线, 是重心.如果
是重心.如果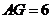 ,那么线段
,那么线段 的长为( )
的长为( )
A.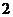 B.
B.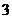 C.
C.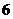 D.
D.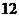
16.在下列命题中,真命题是( )
A.两条对角线相等的四边形是矩形
B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相平分的四边形是平行四边形
D.两条对角线互相垂直且相等的四边形是正方形
三.(本大题共5题,满分48分)
17.(本题满分9分)
先化简,再求值: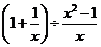 ,其中
,其中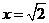 .
.
18.(本题满分9分)
解方程组: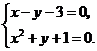
19.(本题满分10分,每小题满分各5分)
已知:如图3,在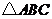 中,
中,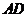 是边
是边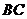 上的高,
上的高,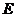 为边
为边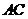 的中点,
的中点,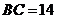 ,
,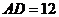 ,
,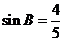 .求(1)线段
.求(1)线段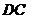 的长;(2)
的长;(2)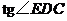 的值.
的值.

20.(本题满分10分,第(1)小题满分3分,第(2)小题满分4分,第(3)小题满分3分)
某市在中心城区范围内,选取重点示范路口进行交通文明状况满意度调查,将调查结果的满意度分为:不满意、一般、较满意、满意和非常满意,依次以红、橙、黄、蓝、绿五色标识.今年五月发布的调查结果中,橙色与黄色标识路口数之和占被调查路口总数的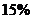 .结合未画完整的图4中所示信息,回答下列问题:
.结合未画完整的图4中所示信息,回答下列问题:
(1)此次被调查的路口总数是__________;
(2)将图4中绿色标识部分补画完整,并标上相应的路口数;
(3)此次被调查路口的满意度能否作为该市所有路口交通文明状况满意度的一个随机样本?
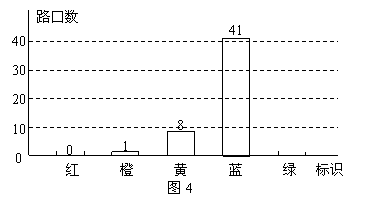 答:____________________.
答:____________________.
21.(本题满分10分)
 本市新建的滴水湖是圆形人工湖.为测量该湖的半径,小杰和小丽沿湖边选取
本市新建的滴水湖是圆形人工湖.为测量该湖的半径,小杰和小丽沿湖边选取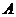 ,
,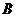 ,
,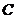 三根木柱,使得
三根木柱,使得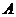 ,
,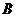 之间的距离与
之间的距离与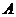 ,
,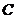 之间的距离相等,并测得
之间的距离相等,并测得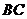 长为
长为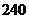 米,
米,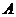 到
到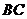 的距离为
的距离为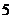 米,如图5所示.请你帮他们求出滴水湖的半径.
米,如图5所示.请你帮他们求出滴水湖的半径.
四.(本大题共4题,满分50分)
22.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)
如图6,在直角坐标系中,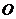 为原点.点
为原点.点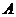 在第一象限,它的纵坐标是横坐标的3倍,反比例函数
在第一象限,它的纵坐标是横坐标的3倍,反比例函数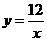 的图象经过点
的图象经过点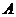 .
.
(1)求点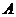 的坐标;
的坐标;
 (2)如果经过点
(2)如果经过点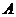 的一次函数图象与
的一次函数图象与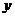 轴的正半轴交于点
轴的正半轴交于点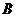 ,且
,且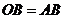 ,求这个一次函数的解析式.
,求这个一次函数的解析式.
23.(本题满分12分,每小题满分各6分)
已知:如图7,在梯形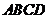 中,
中,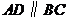 ,
,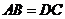 .点
.点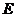 ,
,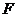 ,
, 分别在边
分别在边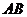 ,
,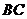 ,
,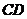 上,
上,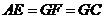 .
.
(1)求证:四边形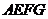 是平行四边形;
是平行四边形;
 (2)当
(2)当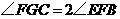 时,求证:四边形
时,求证:四边形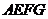 是矩形.
是矩形.
24.(本题满分12分,第(1)小题满分5分,第(2)小题满分3分,第(3)小题满分4分)
如图8,在直角坐标系中,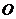 为原点.点
为原点.点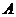 在
在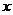 轴的正半轴上,点
轴的正半轴上,点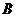 在
在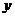 轴的正半轴上,
轴的正半轴上,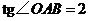 .二次函数
.二次函数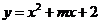 的图象经过点
的图象经过点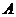 ,
,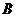 ,顶点为
,顶点为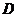 .
.
(1)求这个二次函数的解析式;
(2)将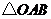 绕点
绕点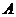 顺时针旋转
顺时针旋转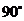 后,点
后,点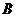 落到点
落到点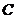 的位置.将上述二次函数图象沿
的位置.将上述二次函数图象沿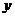 轴向上或向下平移后经过点
轴向上或向下平移后经过点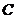 .请直接写出点
.请直接写出点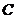 的坐标和平移后所得图象的函数解析式;
的坐标和平移后所得图象的函数解析式;
 (3)设(2)中平移后所得二次函数图象与
(3)设(2)中平移后所得二次函数图象与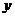 轴的交点为
轴的交点为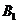 ,顶点为
,顶点为 .点
.点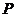 在平移后的二次函数图象上,且满足
在平移后的二次函数图象上,且满足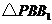 的面积是
的面积是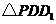 面积的
面积的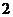 倍,求点
倍,求点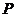 的坐标.
的坐标.
25.(本题满分14分,第(1)小题满分4分,第(2)小题满分7分,第(3)小题满分3分)
已知点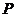 在线段
在线段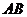 上,点
上,点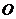 在线段
在线段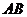 延长线上.以点
延长线上.以点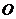 为圆心,
为圆心,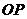 为半径作圆,点
为半径作圆,点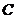 是圆
是圆 上的一点.
上的一点.
(1)如图9,如果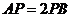 ,
,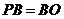 .求证:
.求证: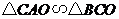 ;
;
(2)如果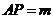 (
(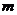 是常数,且
是常数,且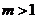 ),
),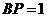 ,
,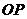 是
是 ,
, 的比例中项.当点
的比例中项.当点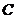 在圆
在圆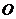 上运动时,求
上运动时,求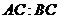 的值(结果用含
的值(结果用含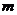 的式子表示);
的式子表示);
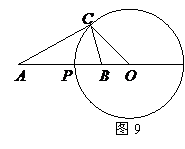 (3)在(2)的条件下,讨论以
(3)在(2)的条件下,讨论以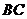 为半径的圆
为半径的圆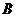 和以
和以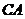 为半径的圆
为半径的圆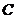 的位置关系,并写出相应
的位置关系,并写出相应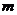 的取值范围.
的取值范围.