2006年黄冈密卷中考押题卷数学
(满分: 120分 测试时间: 120分钟)
一、填空题(每小题3分, 共24分)
1. 3-2的绝对值是___________; -3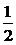 的倒数是____________; 近似数0.00043用科学记数法表示的结果为________________________.
的倒数是____________; 近似数0.00043用科学记数法表示的结果为________________________.
2. 化简:  的结果是________________.
的结果是________________.
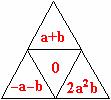
3. 如图, 沿大正三角形的对称轴对折, 则互相重合的两个小正三角形内的式子的乘积为______________________.

(第3题图) (第5题图) (第11题图)
4. 在日常生活中如取款、上网等都需要密码. 有一种用
“因式分解” 法产生的密码,
方便记忆. 原理是: 如对于多项式x4-y4, 因式分解的结果是(x-y)(x+y)(x2+y2).
若取x=9,y=9时, 则各个因式的值是: (x-y)=0,
(x+y)=18, (x2+y2)=162, 于是就可以把
“
5. 图中正比例函数和反比例函数的图象相交于A、B两点, 分别以A、B两点为圆心, 画与y轴相切的两个圆. 若点A的坐标为(1, 2), 则图中两个阴影面积的和是____________.
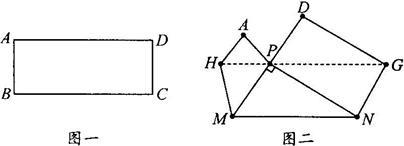
6. 把图一的矩形纸片ABCD折叠, B、C两点恰好重合落在AD边上的点P处(如图二), 已知∠MPN=900, PM=3, PN=4, 那么矩形纸片ABCD的面积为__________.
二、单项选择题(每小题3分, 共18分)
( ) 7. 如下图是甲、乙、丙三人玩跷跷板的示意图(支点在中点处), 则甲的体重的取值范围在数轴上表示正确的是

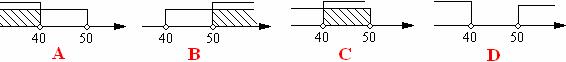
( ) 8. 下列四幅图形中, 表示两棵小树在同一时刻阳光下的影子的图形可能是

( ) 9. 如下左图是一个立方体图形的二视图, 根据图示的数据求出这个立方体图形的体积是
A.
24 cm3 B.
cm3 B.
 cm3 C.
72
cm3 C.
72 cm3 D.
192
cm3 D.
192 cm3
cm3
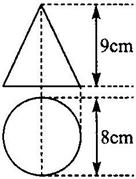
(第9题图) (第10题图)
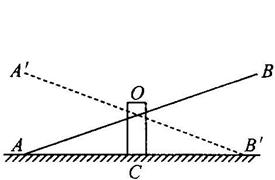
( ) 10. 如上右图是跷跷板的示意图, 支柱OC与地面垂直, 点O是横板AB的中点, AB可可绕着点O上下转动, 当A端落地时, ∠OAC=200, 横板上下可转动的最大角度(即∠A’OA)是
A. 800 B. 600 C. 400 D. 200
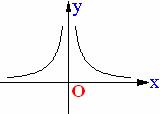
( ) 11. 如图所示的函数图象的关系式可能是
A.
y=x B.
y=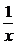 C.
y=x2 D.
y=
C.
y=x2 D.
y=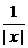
( ) 12. 在5×5方格纸中将图甲中的图形N平移后的位置如图乙所示, 那么正确的平移方法是
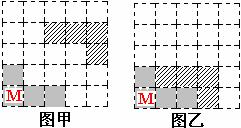
A. 先向下移动1格, 再向左移动1格 B. 先向下移动1格, 再向左移动2格
C. 先向下移动2格, 再向左移动1格 D. 先向下移动2格, 再向左移动2格
三、解答题(共20分)
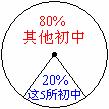 13.
(8分) 黄冈市从2006年年初取消初中生上早晚自习后, 学生的综合素质状况受到全社会的广泛关注. 黄冈市有关部门对全市初中九年级9200名学生数学学业考试状况进行了一次抽样调查, 从中随机抽查了5所初中九年级全体学生的数学调考成绩, 右图是2006年3月抽样情况统计图. 这5所初中的九年级学生的得分情况如下表(数学学业考试满分120分)
13.
(8分) 黄冈市从2006年年初取消初中生上早晚自习后, 学生的综合素质状况受到全社会的广泛关注. 黄冈市有关部门对全市初中九年级9200名学生数学学业考试状况进行了一次抽样调查, 从中随机抽查了5所初中九年级全体学生的数学调考成绩, 右图是2006年3月抽样情况统计图. 这5所初中的九年级学生的得分情况如下表(数学学业考试满分120分)
(1)这5所初中九年级学生的总人数有多少人?
(2)统计时, 老师漏填了表中空白处的数据, 请你帮老师填上:
分数段
频数
频率
72分以下
736
0.4
72―80分
276
0.15
81―95分
96―108分
300
0.2
109―119分
120分
5
(3)随机抽取一人, 恰好是获得120分的概率是多少?
(4)从上表中, 你还能获得其他的信息吗? (写出一条即可)
14. (6分) 小明在银行存入一笔零花钱. 已知这种储蓄的年利率为n%, 若设到期后的本息和(本金+利息)为y (元), 存入的时间为x (年), 那么
(1)下列哪个图象更能反映y与x之间的函数关系? 从图中你能看出存入的本金是多少元? 一年后的本息和是多少元?

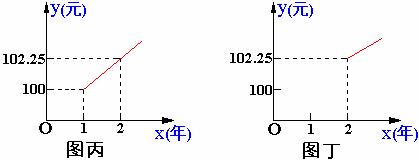
(2)根据(1)的图象, 求出y与x的函数关系式(不要求写出自变量x的取值范围), 并求出两年后的本息和.
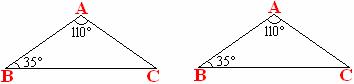
15. (6分) 如图, 在△ABC中, ∠A=1100, ∠B=350, 请你应用变换的方法得到一个三角形使它与△ABC全等, 且要求得到的三角形与原△ABC组成一个四边形.
(1)要求用两种变换方法解决上述问题;(写出变换名称, 画出图形即可)
(2)指出四边形是什么图形? (不要求证明)
说明: 如果两种平移变换方法解决此题算一种变换; 两种变换是指平移、旋转等不同变换.
四、多项选择题(本题满分8分. 在每个小题所给四个选项中, 至少有一项符合题目要求, 请选出. 全对得4分; 对而不全的酌情扣分; 有对有错、全错或不答的均不得分.)
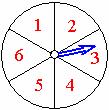
( ) 16. 如图所转盘被划分成六个相同大小的扇形, 并分别标出1、2、3、4、5、6这六个数字, 指针停在每个扇形的可能性相等, 四位同学各自发表了下述见解:
甲: 如果指针前三次都停在了3号扇形, 下次就一定不会停在3号扇形了;
乙: 只要指针连续转六次, 一定会有一次停在6号扇形;
丙: 指针停在奇数号扇形的概率和停在偶数号扇形的概率相等;
丁: 运气好的时候, 只要在转动前默默想好让指针停在6号扇形, 指针停在6号扇形的可能性就会加大.
其中你认为错误的见解有
A. 甲 B. 乙 C. 丙 D. 丁
(第16题图) (第17题图)
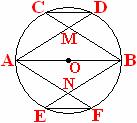
( ) 17. 如图, AB是⊙O的直径, C、E是圆周上关于AB对称的两个不同点, CD//AB//EF, BC与AD交于M, AF与BE交于N. 在A、B、C、D、E、F、M、N中, 能构成矩形的四个点有
A. C、E、F、D B. A、E、B、D C. A、F、B、C D. A、M、B、N
五、解答题(共50分)
18. (9分) 我们做一个拼图游戏: 用等腰直角三角形拼正方形. 请按下面规则与程序操作:
第一次: 将两个全等的等腰直角三角形拼成一个正方形;
第二次: 在前一个正方形的四条边上再拼上四个全等的等腰直角三角形(等腰直角三角形的斜边与正方形的边长相等), 形成一个新的正方形; 以后每次都重复第二次的操作.
(1)请你在第一次拼成的正方形的基础上, 画出第二次和第三次拼成的正方形图形;
(2)若第一次拼成的正方形的边长为a, 请你根据操作过程中的观察思考填写下表:
操 作 次 数 ( n )
1
2
3
4
……
n
每次拼成的正方形面积(S)
a2
……
19. (8分) 某家庭装饰厨房需用480块某品牌的同一种规格的瓷砖, 装饰材料商场出售的这种瓷砖有大、小两种包装, 大包装每包50片, 价格为30元; 小包装每包30片, 价格为20元, 若大、小包装均不拆开零售, 那么怎样制定购买方案才能使所付费用最少?
20.
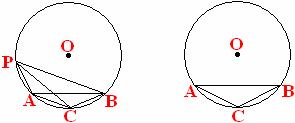
(10分) 如图, 点P是圆上的一个动点, 弦AB=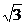 , PC是∠APB的平分线,
∠BAC=300. (1)当∠PAC等于多少度时, 四边形PACB有最大面积? 最大面积是多少? (2)当∠PAC等于多少度时, 四边形PACB是梯形? 说明你的理由.
, PC是∠APB的平分线,
∠BAC=300. (1)当∠PAC等于多少度时, 四边形PACB有最大面积? 最大面积是多少? (2)当∠PAC等于多少度时, 四边形PACB是梯形? 说明你的理由.
21. (10分) 市移动通讯公司开设了两种通讯业务: “全球通” 使用者先缴50元月基础费, 然后每通话1分钟, 再付电话费0.4元; “神州行” 不缴月基础费, 每通话1分钟, 付话费0.6元(这里均指市内通话). 若一个月内通话x分钟, 两种通讯方式的费用分别为y1元和y2元.
(1)写出y1、y2与x之间的函数关系式; (2)一个月内通话多少分钟, 两种通讯方式的费用相同? (3)若某人预计一个月内使用话费200元, 则应选择哪种通讯方式较合算?
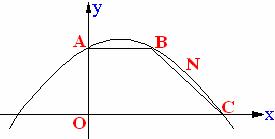
22. (13分) 如图, 在平面直角坐标系中有一直角梯形OABC, ∠AOC=900, AB//OC, OC在x轴上, 过A、B、C三点的抛物线表达式为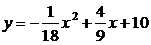 .
.
(1)求A、B、C三点的坐标; (2)如果在梯形OABC内有一矩形MNPO, 使M在x轴上, N在BC边上, P在OC边上, 当MN为多少时, 矩形MNPO的面积最大? 最大面积是多少? (3)若用一直线将梯形OABC分为面积相等的两部分, 试说明你的方法. (注: 总结出一般规律得满分, 若用特例说明, 有四种且正确也可得满分)