2006年中等学校招生考试(大纲卷)
第Ⅰ卷
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得4分,选错、不选或选出的答案超过一个均记零分.
1.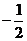 的绝对值是
的绝对值是
(A)-2
(B) 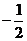 (C)2
(D)
(C)2
(D)
2.下列计算正确的是
(A)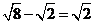 (B)
(B)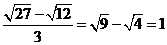
(C)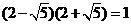 (D)
(D)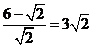
3.若反比例函数 的图像经过点(-1 , 2 ),则这个函数的图像一定经过点
的图像经过点(-1 , 2 ),则这个函数的图像一定经过点
(A)(2,-1)
(B)(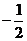 ,2)
(C)(-2,-1) (D)(
,2)
(C)(-2,-1) (D)( ,2)
,2)
4.钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是
(A)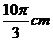 (B)
(B) 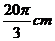 (C)
(C)  (D)
(D)
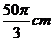
5.已知方程组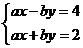 的解为
的解为 ,则2a-3b的值为
,则2a-3b的值为
(A)4 (B)6 (C)-6 (D)-4
6.小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是
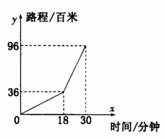
(A) 37.2分钟 (B) 48分钟 (C ) 30分钟 ( D )33分钟
7.如图,路灯距地面 8 米,身高 1 . 6 米的小明从距离灯的底部(点O ) 20米的点A处,
沿AO所在的直线行走14米到点B时,人影长度

(A)变长3.5 米 (B)变长2.5米
(C)变短3.5米 (D)变短2.5米
8.如图,B是线段AC的中点,过点C的直线l与AC成600的角,在直线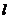 上取一点P,使∠APB=300,则满足条件的点P的个数是
上取一点P,使∠APB=300,则满足条件的点P的个数是

(A) 3个 (B) 2个
(C) l个 (D)不存在
9.若方程3x2-10x + m = 0有两个同号不等的实数根,则m的取值范围是
(A) m≥0 (B) m >0
(C)0<m<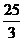 (D) 0<m≤
(D) 0<m≤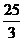
10.在△ABC中,BM=6,点A, C, D分别在MB,BN,NM上,四边形ABCD为平行四边形,∠NDC=∠MDA,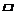 ABCD的周长是
ABCD的周长是
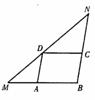
(A)24 (B)18 (C)16 (D)12
11.在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形又能拼成三角形和梯形的是

12.已知点A(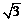 ,1) , B (0 , 0) ,C (
,1) , B (0 , 0) ,C (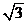 ,0)
, AE平分∠BAC,交BC于点E,则直线AE对应的函数表达式是
,0)
, AE平分∠BAC,交BC于点E,则直线AE对应的函数表达式是
(A)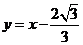 (B)y=x-2
(C)
(B)y=x-2
(C)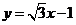 (D)
(D)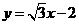
第Ⅱ卷
二、填空题:本大题共6小题,共24分,只要求填写最后结果,每小题填对得4分.
13.随着中国综合国力的提升,近年来全球学习汉语的人数不断增加.据报道,2005年海外学
习汉语的学生人数已达38 200 000人),用科学记数法表示为 人(保留 3 个有效数字).
14.已知⊙O1,和⊙O2的半径分别为3cm 和5cm ,两圆的圆心距O1O2=6cm,则两圆的位置关系
是 .
15.计算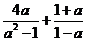 的结果是
.
的结果是
.
16.要在一个矩形纸片上画出半径分别是4cm和1cm的两个外切圆,该矩形纸片面积的最小值
是 .
17.在平面直角坐标系中,已知点P0的坐标为(1, 0 ),将点P0绕着原点O按逆时针方向旋转600得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转600得点P3,则点P3的坐标是 .
18.右图是由9个等边三角形拼成的六边形,若已知中间的小等边三角形
的边长是a,则六边形的周长是 .
三、解答题:本大题共7小题,共78分,解答要写出必要的文字说明、证明过程或演算步骤.
19.(本题满分8分)
解不等式组,并把其解集在数轴上表示出来:
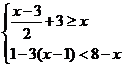
20.(本题满分10分)
某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
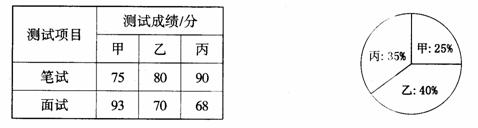
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如上图所示,每得一票记作1分.
(l)请算出三人的民主评议得分;
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到 0.01 )?
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按 4 : 3 : 3 的比例确定个人成绩,那么谁将被录用?
21.(本题满分12分)

近年来,由于受国际石油市场的影响,汽油价格不断上涨.请你根据下面的信息,帮小明计算今年5月份汽油的价格.
22.(本题满分 12 分)
两个全等的含300, 600角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连结BD,取BD的中点M,连结ME,MC.试判断△EMC的形状,并说明理由.

23.(本题满分12分)
已知关于x的二次函数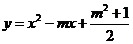 与
与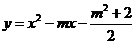 ,这两个二次函数的图像中的一条与x轴交于A, B两个不同的点.
,这两个二次函数的图像中的一条与x轴交于A, B两个不同的点.
(l)试判断哪个二次函数的图像经过A, B两点;
(2)若A点坐标为(-1, 0),试求B点坐标;
(3)在(2)的条件下,对于经过A, B两点的二次函数,当x取何值时,y的值随x值的增大而减小?
24.(本题满分12分)
如图,在△ABC中,AB=AC=1,点D,E在直线BC上运动.设BD=x, CE=y
(l)如果∠BAC=300,∠DAE=l050,试确定y与x之间的函数关系式;

(2)如果∠BAC=α,∠DAE=β,当α, β满足怎样的关系时,(l)中y与x之间的函数关系式还成立?试说明理由.
25.(本题满分12分)
半径为2.5的⊙O中,直径AB的不同侧有定点C和动点P.已知BC :CA=4 : 3,点P在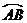 上运动,过点C作CP的垂线,与PB的延长线交于点O
上运动,过点C作CP的垂线,与PB的延长线交于点O
(l)当点P与点C关于AB对称时,求CQ的长;
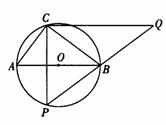
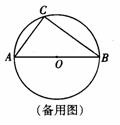
(2)当点P运动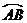 到的中点时,求CQ的长;
到的中点时,求CQ的长;
(3)当点P运动到什么位置时,CQ取到最大值?求此时CQ的长.