2005年湖北省黄冈市初中升学统一考试
(非课改区)
第一卷
一、填空题(每空3分,共24分)
1.的相反数是 ,立方等于? 64的数是 ,将x ? xy 2分解因式的结果是 ;
2.反比例函数y = 的图像经过点(tan45°,cos60°),则k = ;
3.方程的解为 ;
4.吕晓同学想利用树影的长测量校园内一棵大树的高度,他在某一时刻测得一棵小树的高为1.5米,其影长为1.2米,同时,他测得这棵大树的影长为3米,则这棵大树的实际高度为 米;
5.某同学在电脑中打出如下排列的若干个圆(图中●表示实心圆,○表示空心圆):
● ○●●○●●●○●●●●○●●●●●○●●●●●●○
若将上面一组圆依此规律复制得到一系列圆,那么前2005个圆中有 个空心圆;
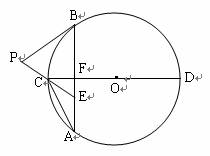
6.已知点P是半径为2的⊙O外一点,PA是⊙的切线,切点为A,且PA = 2,在⊙O内作长为2的弦AB,连结PB,则PB的长为 ;
二、单项选择题(请将下列各题中唯一正确的答案序号填入题后的刮号里,不填、错填或多填均不得分,每小题3分,共15分)
7.已知x、y为实数,且+ 3(y ? 2)2 = 0,则x ? y的值为( )
A.3 B.? 3 C.1 D.? 1
8.下列运算中正确的是( )
A.x 5 + x 5 = 2x 10
B.? (? x ) 3 ?(? x ) 5 = ? x 8
C.(? 2x 2y) 3?4x ? 3 = ? 24x 3y 3
D.( x ? 3 y) (? x + 3y ) = x 2 ? 9 y 2
|
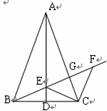
 10.如图,在 ABCD中,EF∥AB,DE∶EA = 2∶3,EF = 4,则CD的长为( )
10.如图,在 ABCD中,EF∥AB,DE∶EA = 2∶3,EF = 4,则CD的长为( )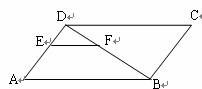

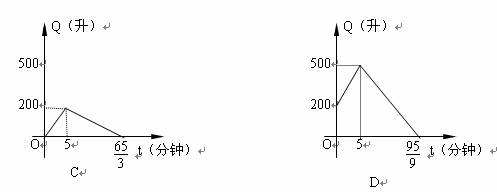
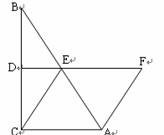
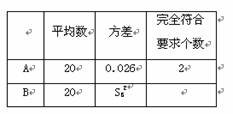


 四、选择题(本题满分8分,在每个小题所给的四个选项中,至少有一项是符合题目要求的,请把所有符合题目要求的答案序号填入题后的刮号内,全对得4分,对而不全的酌情扣分;有对有错,全错或不答的均不得分)
四、选择题(本题满分8分,在每个小题所给的四个选项中,至少有一项是符合题目要求的,请把所有符合题目要求的答案序号填入题后的刮号内,全对得4分,对而不全的酌情扣分;有对有错,全错或不答的均不得分)