1.已知：|x|=3，|y|=2，且xy＜0，则x+y的值等于______.

　　2.设a-b=2+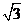，b-c=2-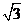，则a²+b²+c²-ab-bc-ac的值为______.

　　3.已知实数x₁，x₂满足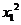-6x₁+2=0和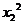-6x₂+2=0，求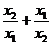的值为______.

　　4.如果一次函数y=mx+n与反比例函数的图象相交于点(,2)，那么该直线与双曲线的另一个交点为______.

　　5.如图1，要把边长为6的正三角纸板剪去三个三角形，得到正六边形，则它的边长为___.

　　6.如图2，直角梯形ABCD的中位线EF的长为a，垂直于底的腰AB的长为b，则图中阴影部分的面积为______.

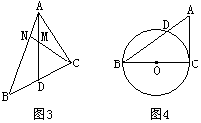
　　7.如图3，在△ABC中，AD是BC边上的中线，M是AD的中点，CM的延长线交AB于N，则AN:AB的值为______.

　　8.如图4，BC是⊙O的直径，AC切⊙O于点C，AB交⊙O于点D，若AD:DB=2:3，AC=10，sinB的值为_____.

　　1.已知|a+b|+|a-b|-2b=0，在数轴上给出关于a，b的四种位置关系如图所示，则可能成立的有(　)

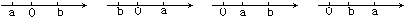
　　(A)1种　　　　　　(B)2种　　　　　　(C)3种　　　　　　(D)4种

　　2.已知a、b、c均为正数，方程ax²+bx+c=0有实根，则方程acx²+b²x+ac=0(　)

　　(A)有两个不相等的正根　　　　　　　 (B)有一个正根，一个负根

　　(C)不一定有实根　　　　　　　　　　 (D)有两个不相等的负根

　　3.当k取任何实数时，抛物线y=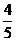(x-k)²+k²的顶点所在曲线是(　)

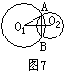
　　(A)y=x²　　　　　 (B)y=-x²　　　　　(C)y=x²(x＞0)　　 (D)y=-x²(x＞0)

　　4.如图5，已知AB⊥CD，△ABD、△BCE都是等腰直角三角形，如果CD=8，BE=3，则AC等于(　)

　　(A)8　　　　(B)5　　　　(C)3　　(D)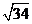

　　5.如图6，ABCD是正方形，E是CD的中点，P是BC上的一点，下列条件中，不能推出△ABP与△ECP相似的有(　)

　　①∠APB=∠EPC　　②∠APE=90°　　③P是BC的中点　　④BP:BC=2:3

　　(A)1个　　　　　　(B)2个　　　　　　(C)3个　　　　　　(D)4个

　　6.如图7，已知⊙O₁与⊙O₂相交于A、B，已知两圆的半径r₁=10，r₂=17，圆心距O₁O₂=21，则公共弦等于(　)

　　(A)2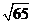　　　　　(B)16　　　　　　 (C)6　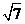　　　　　(D)17

　　1.(12分)已知关于x的一元二次方程ax²+bx+c=0没有实数根.甲由于看错了二次项系数，误求得两根为2和4；乙由于看错了某项系数的符号，误求得两根为-1和4，求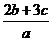的值.

　　2.(12分)如图8，正方形表示一张纸片，根据要求需多次分割，把它分割成若干个直角三角形.操作过程如下：第一次分割，将正方形纸片分成4个全等的直角三角形，第二次分割将上次得到的直角三角形中一个再分成4个全等的直角三角形；以后按第二次分割的作法

进行下去.

　　(1)请你设计出两种符合题意的分割方案图;

分割次数(n)

1

2

3

…

最小直角三角形的面积(S)

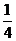a²

…

　　(3)在条件(2)下，请你猜想：分割所得的最小直角三角形面积S与分割次数n有什么关系？用数学表达式表示出来.

　　3.(17分)某中学预计用1500元购买甲商品x个，乙商品y个，不料甲商品每个涨价1.5元，乙商品每个涨价1元，尽管购买甲商品的个数比预定减少10个，总金额多用29元.又若甲商品每个只涨价1元，并且购买甲商品的数量只比预定数少5个，那么买甲、乙两商品支付的总金额是1563.5元.

　　(1)求x、y的关系式；

　　(2)若预计购买甲商品的个数的2倍与预计购买乙商品的个数的和大于205，但小于210，求x，y的值.

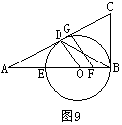
　　4.(17分)如图9，在△ABC中，∠ABC=90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，AD=2，AE=1.

　　(1)求△AOD和△BCD的面积；

　　(2)若F是线段BE上任一点，FG⊥AG，G是垂足，设线段CG和OF的长分别是x和y，试写出y与x之间的关系式.(不要求写出x的取值范围).