2005年全国初中数学联赛山东赛区预赛暨
2004年山东省初中数学竞赛试题
2004年11月26日
一、选择题(本题共8分,每小题6分,满分48分):下面各题给出的选项中,只有一项是正确的,清江正确选项的代号填在题后的括号内.
1. 已知n是奇数,m是偶数,方程组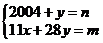 有整数解x0,y0,则( )
有整数解x0,y0,则( )
A.x0,y0均为偶数 B. x0,y0均为奇数 C. x0是偶数,y0是奇数 D. x0是奇数,y0是偶数
2. 若ab≠0,则等式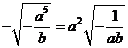 成立的条件是( )
成立的条件是( )
A.a>0,b>0 B.a<0,b<0 C.a>0,b<0 D.a<0,b<0
3. 设a, b, c, d都是非零实数,则四个数:-ab, ac, bd, cd ( )
A.都是正数 B.都是负数 C.是两正两负 D.是一正三负或一负三正
4.矩形ABCD中,AB=a, BC=b,M是BC的中点,DE⊥AM, E为垂足,则DE= ( )
A. 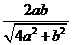 B.
B. 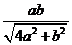 C.
C. 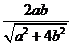 D.
D. 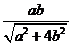
5. 某商店出售某种商品每件可获利m元,利润率为20%(利润率= ),若这种商品的进价提高25%,而商店将这种商品的售价提高到每件仍可获利m元,则提价后的利润率为( )
),若这种商品的进价提高25%,而商店将这种商品的售价提高到每件仍可获利m元,则提价后的利润率为( )
A.25% B.20% C.16% D.12.5%
6. 在△ABC中,∠ABC=900,∠A=200, 将△ABC绕点A按逆时针方向旋转角α到△A′B′C的位置,其中A′,B′分别是A, B的对应点,B在A′B′上,CA′交AB于D,则∠BDC的度数为( )
A.400 B.450
C.450 D.600
7. 若x0是一元二次方程ax2+bx+c=0(a≠0)的根,则判别式△=b2-4ac与平方式M=(2ax0+b)2的大小关系是( )
A.△>M B. △=M C. △<M D.不能确定
8. 在△ABC中,a, b, c分别是∠A, ∠B, ∠C的对边,若∠B=600,则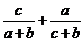 的值为( )
的值为( )
A.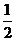 B.
B.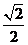 C.1 D.
C.1 D.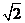
二、填空题(本题共4小题,每小题8分,满分32分),将答案直接填写在对应题目中的横线上
9. 若x1,x2都满足条件|2x-1|+|2x+3|=4,且x1<x2,则x1-x2的取值范围为 .
10. 已知a, b是方程x2-4x+m=0的两个根,b,c是方程x2-8x+5m=0的两个根,
则m= .
11. 在△ABC中,D, E分别在边AB, AC上,且DE//BC, 过点A作平行于BC的直线分别交CD和BE的延长线于点M, N, 若DE=2, BC=6, 则MN= .
12. 如图,在矩形ABCD中,AB=5, BC=12, 将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖桌面的面积是 .
三、解答题(本题共3小题,每小题20分,满分60分)
13. 甲、一辆汽车零售商(以下分别简称甲、乙)向某品牌汽车生产厂订购一批汽车,甲开始订购的汽车数量是乙订购数量的3倍,后来由于某种原因,甲从其所定的汽车中转让给乙6辆,在提车时,生产厂所提供的汽车比甲、乙所订购的总数少了6辆,最后甲所购汽车的数量是乙所购的2倍. 试问:甲、乙最后所购的汽车总数至多是多少辆?又至少是多少辆?
14.已知三个边长相等的正方形相邻并排,求∠EBF+∠EBG
15. 从1,2,3,……,2004中任选K-1个数中,一定可以找到能构成三角形边长的三个数(这里要求三角形三边长互不相等),试问满足条件的K的最小值是多少?