三原南郊中学2007---2008学年度上学期期中考试
高一数学试题
一、选择题(每题5分,共60分)
1.已知集合 ,
,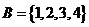 ,则
,则 等于( )
等于( )
A.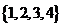 B.
B. C.
C.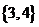 D.
D.
2.函数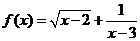 的定义域为( )
的定义域为( )
A.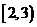 B.
B.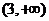
C. D.
D.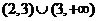
3.已知 ,
,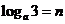 ,则
,则 等于( )
等于( )
A.6 B.
4.二次函数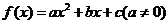 ,若二次方程
,若二次方程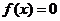 的两个不等实数解为
的两个不等实数解为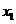 ,
, ,且
,且 ,则
,则 的值为( )
的值为( )
A.大于0 B.小于0 C.等于0 D.不确定
5.有一组实验数据如下:
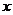
1.99
3.0
4.0
5.1
6.12
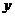
1.50
4.04
7.51
12.50
18.12
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的是( )
A.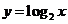 B.
B. C.
C.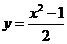 D.
D.
 6.若偶函数
6.若偶函数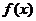 的定义域为区间
的定义域为区间 ,且函数在区间
,且函数在区间 上的图象如下,则不等式
上的图象如下,则不等式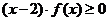 的解集为(
)
的解集为(
)
A. B.
B.
C.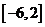 D.
D.
7.函数 在区间
在区间 上的最大值为4,则
上的最大值为4,则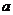 等于( )
等于( )
A.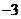 B.
B. C.3 D.
C.3 D.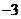 或
或
8.设 ,且
,且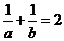 ,则
,则 等于(
)
等于(
)
A.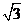 B.
B. C.
C. D.
D.
9.已知函数 的图象与函数
的图象与函数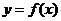 的图象关于直线
的图象关于直线 对称,则
对称,则 等于(
)
等于(
)
A. B.
B. C.
C.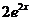 D.
D.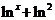
10.已知函数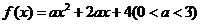 ,若
,若 ,且
,且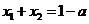 ,则
,则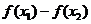 是( )
是( )
A.大于0 B.小于0 C.等于0 D.不确定
11.已知集合 ,
, ,则
,则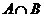 等于( )
等于( )
A. B.
B.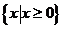
C.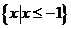 D.
D.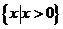
12.某企业去年年销售收入1000万元,年成本分为生产成本500万元与年广告费成本200万元两部分。若利润的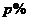 为国税,且年广告费超出年销售收入2%的部分也必须按
为国税,且年广告费超出年销售收入2%的部分也必须按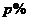 征国税,其它不纳税。已知该企业去年共纳税120万元,则税率
征国税,其它不纳税。已知该企业去年共纳税120万元,则税率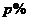 为( )
为( )
A.10% B.12% C.25% D.40%
二、填空题(每题4分,共16分)
13.幂函数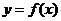 的图象过点
的图象过点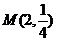 ,则
,则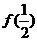 的值=
的值=
14.函数 的定义域是
的定义域是
15.方程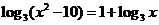 的解是
的解是
16.三个数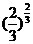 ,
,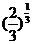 ,
, 的大小关系用“<”表示是
的大小关系用“<”表示是
三、解答题
17.(12分)已知集合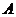 中的元素都是实数,且当
中的元素都是实数,且当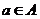 时,一定有
时,一定有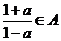
(1)若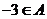 ,求出
,求出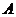 中其它可能有的元素;
中其它可能有的元素;
(2)证明: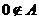
18.(12分)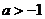 ,求函数
,求函数 在区间
在区间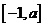 上的最大值
上的最大值
19.(12分)函数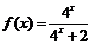
(1)若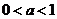 ,求
,求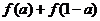 的值;
的值;
(2)求 的值
的值
20.(12分)计算下列各式的值
(1)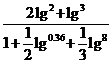 (2)
(2)
21.(12分)设函数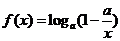 ,其中
,其中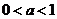
(1)求满足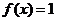 的
的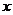 值
值
(2)用函数单调性定义证明: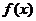 在区间
在区间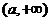 上是减函数
上是减函数
22.(14分)某产品每件成本是120元,试销阶段每件产品的销售价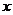 (元)与产品的日销售量
(元)与产品的日销售量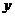 (件)之间的关系如下表:
(件)之间的关系如下表:
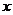
130
150
165
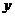
70
50
35
且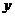 是
是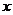 的一次函数.
的一次函数.
要使每日获得的总利润 (元)最大,则每件产品的销售价
(元)最大,则每件产品的销售价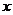 (元)应为多少?(利润=销售价
(元)应为多少?(利润=销售价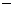 成本价)每日最大利润是多少元?
成本价)每日最大利润是多少元?
三原南郊中学2007---2008学年度上学期期中考试
高一数学答题纸
二、填空题
13. 14.
15. 16.
三、解答题
17.
18.
19.
20.
21.
22.