银川一中2007届高三年级第三次模拟考试
数 学 试 卷(文)
命题教师:王孝贤
一、选择题(每题5分,共60分)
1.函数y= 的定义域为( )
的定义域为( )
A.{x|x≠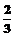 } B.(
} B.(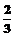 ,+∞) C.(-∞,
,+∞) C.(-∞,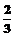 ) D.[
) D.[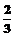 ,+∞]
,+∞]
2.复数z1=1+i,z2=x+2i(x∈R),若z1z2∈R,则x=( )
A.-2 B.
3.已知样本10,8,6,10,13,8,10,12,11,7,8,9,11,9,12,9,10,11,12,12,那么频率是0.3的范围是( )
A.5.5~7.5 B.7.5~
4.下列函数中,在定义域内既为奇函数又为减函数的是( )
A.y=sin2x B.y=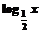 C.y=2x D.y=-2x3
C.y=2x D.y=-2x3
5.函数y=cos2(2x+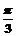 )-sin2(2x+
)-sin2(2x+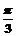 )的最小正周期是( )
)的最小正周期是( )
A. B.
B. C.4
C.4 D.
D.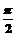
6.随着x的增大:①y=logax(a>1)的值增长的越来越慢 ②y=ax(a>1)的值增长速度越来越快,会表现为指数爆炸 ③y=kx+b(k>0)的值匀速增长 ④y=2x增长速度会超过并远远大于y=x2的增长速度,以上结论,正确的个数是( )
A.1 B.2 C.3 D.4
7.由点P(2,4)向直线ax+y+b=0引垂线,垂足为Q(4,3),则a,b的值依次为( )
A.-2,5 B.2,-11 C.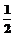 ,-5 D.-
,-5 D.-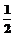 ,-11
,-11
8.先后抛掷三枚均匀的一角、伍角、壹元的硬币,则出现两枚正面,一枚反面的概率是( )
A.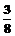 B.
B.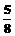 C.
C. D.
D.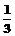
9.以下结论不正确的是( )
A.根据2×2列联表中的数据计算得出k2≥6.635,而P(k2≥6.635)≈0.01,则有99%的把握认为两个分类变量有关系
B.在线性回归分析中,相关系数为r,|r|越接近于1,相关程度越大;|r|越小,相关程度越小
C.在回归分析中,相关指数R2越大,说明残差平方和越小,回归效果越好
D.在回归直线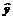 =0.5x-85中,变量x=200时,变量y的值一定是15
=0.5x-85中,变量x=200时,变量y的值一定是15
10.若a,b,c是Rt△的三边(c为斜边)长,则圆x2+y2=2被直线ax+by+c=0截得的弦长为( )
A.1 B.2 C.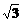 D.2
D.2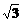
11.设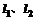 是两条不重合的直线,
是两条不重合的直线,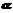 、
、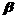 是两个不重合的平面,给出下列四个命题:①若
是两个不重合的平面,给出下列四个命题:①若

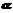 ,
,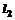

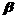 ,
, ∥
∥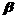 ,
,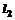 ∥
∥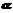 ,则
,则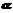 ∥
∥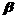 ②
② ⊥
⊥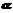 ,
,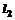 ⊥
⊥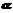 ,则
,则 ∥
∥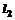 ③若
③若 ⊥
⊥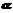 ,
, ⊥
⊥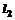 ,则
,则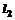 ∥
∥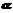 ④若
④若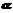 ⊥
⊥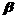 ,
,

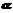 ,则
,则 ⊥
⊥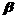 ,其中正确的命题个数为( )
,其中正确的命题个数为( )
A.0 B.1
C.2 D.3
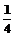
12.下表给出一个“直角三角形数阵”,记第i行, 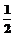
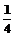
第j列的数为aij,则a83=(
)

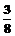
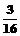
A.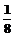 B.
B.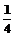 1
1 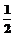
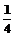
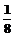
|
 =(-2,3),
=(-2,3), =(1,m),若
=(1,m),若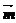 =(cos
=(cos =(cos
=(cos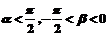 ,|
,|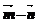 |=
|=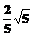 ,
, 求sin(
求sin(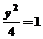 ,直线
,直线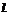 :y=mx+1
:y=mx+1 ,求数列{cn}的前n项和公式Tn。
,求数列{cn}的前n项和公式Tn。 四、选考题(10分,请从所给的二道题中任选一道作答,并用2B铅笔在答题卡上把所选对应题目的题号涂黑)
四、选考题(10分,请从所给的二道题中任选一道作答,并用2B铅笔在答题卡上把所选对应题目的题号涂黑)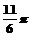 )到直线
)到直线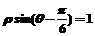 的距离。
的距离。 且m≠-
且m≠- 15.
12 16.
15.
12 16. 
 (3分)
(3分) sin
sin +cos
+cos (6分)
(6分) (10分)
(10分) (12分)
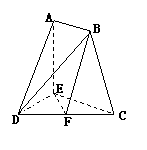
(12分) 方法一:求出EF=
方法一:求出EF= ,BE=
,BE= ,取EC中点G,BG=2,GF=1,BF=
,取EC中点G,BG=2,GF=1,BF= =(1,1,0),
=(1,1,0), =(0,1,2)
=(0,1,2)
 与C恒有两个不同交点 (4分)
与C恒有两个不同交点 (4分) (2分)
(2分) (6分)
(6分) x1+x2+
x1+x2+ =0(∵x1≠x2)
=0(∵x1≠x2) m=0
(9分)
m=0
(9分) )2=
)2= (12分)
(12分) (4+m2)x2+2mx-3=0
(4+m2)x2+2mx-3=0 (10分)
(10分) ,P3=
,P3=


 的等比数列
(10分)
的等比数列
(10分) [1-(-
[1-(- (14分)
(14分) (4分)
(4分) ,q=
,q= (8分)
(8分) [(6n-5)4n+5]
[(6n-5)4n+5] ∴A=[-1,1]
(5分)
∴A=[-1,1]
(5分)
 (10分)
(10分)
 △ABE≌△ACD (5分)
△ABE≌△ACD (5分) △ABC∽△BEC
△ABC∽△BEC  (8分)
(8分) (10分)
(10分) )
P(
)
P( ) (3分)
) (3分) x-
x- y+2=0 (7分)
y+2=0 (7分) (10分)
(10分) ,b=sin
,b=sin