2007年宁波市高三模拟试卷
(数学文科)
说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.
考试时间120分钟.
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中只有一项是符合题目要求的.
1、若全集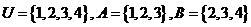 ,则
,则 为( )
为( )
A.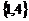 B.
B.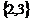 C.
C.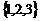 D.
D.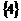
2、已知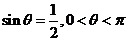 ,则
,则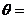
A.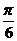 B.
B.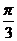 C.
C. D.
D. 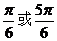
3、函数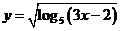 的定义域为( )
的定义域为( )
A.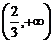 B.
B.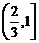 C.
C.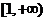 D.
D.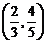
4、已知实数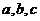 ,则“
,则“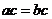 ”是“
”是“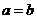 ”的
”的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
5、下列函数中,不是周期函数的是
A.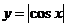 B.
B.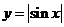 C.
C.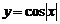 D.
D.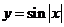
6、给出以下四个命题:
①过直线外一点作该直线的垂线是唯一的;
②过直线外一点作该直线的平行平面是唯一的;
③过平面外一点作该平面的垂直平面是唯一的;
④过平面的斜线作该平面的垂直平面是唯一的.
其中真命题的个数为
A.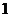 B.
B. C.
C.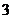 D.
D.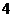
7、5个人站成一排,甲、乙两人之间恰有1人的概率是
A. B.
B.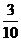 C.
C.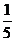 D.
D.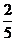
8、已知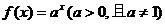 ,
,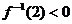 ,则函数
,则函数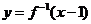 的图象是
的图象是

9、在等差数列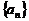 中,
中,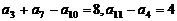 ,记
,记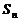 为其前
为其前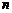 项和,则
项和,则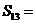
A. 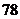 B.
B.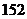 C.
C.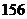 D.
D.
10、已知两点 ,点
,点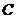 是圆
是圆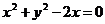 上任意一点,则
上任意一点,则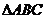 面积的最小值是
面积的最小值是
A. B.
B.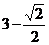 C.
C.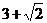 D.
D.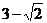
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题7小题,每小题4分,共28分.把答案填在答案卡中的相应横线上.
11、椭圆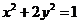 的两条准线间的距离是 ▲ .
的两条准线间的距离是 ▲ .
12、某校高三有理科生共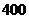 人,文科生若干人,按分层抽样的方法从高三学生中抽出
人,文科生若干人,按分层抽样的方法从高三学生中抽出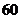 名
名
学生参加问卷调查,其中文科生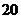 人,则该校共有高三学生 ▲ 人.
人,则该校共有高三学生 ▲ 人.
13、已知实数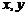 满足条件
满足条件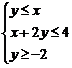 ,则表达式
,则表达式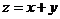 的取值范围是 ▲ .
的取值范围是 ▲ .
14、在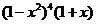 的展开式中,
的展开式中,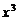 项的系数为 ▲ .
项的系数为 ▲ .
15、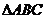 的三内角
的三内角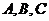 所对的长分别为
所对的长分别为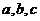 ,若向量
,若向量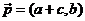
与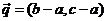 是共线向量,则角
是共线向量,则角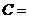 ▲ .
▲ .
16、长方体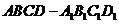 中,底面
中,底面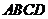 是边长为
是边长为 的正方形,
的正方形,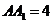 ,
,
则点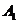 到截面
到截面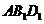 的距离为 ▲ .
的距离为 ▲ .
17、在等比数列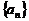 中,
中, 公比
公比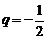 ,设
,设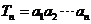 ,则使
,则使 取得最大值的
取得最大值的
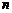 为 ▲ .
为 ▲ .
三、解答题:本大题5小题,其中第18题~第21题每题14分,第22题为16分 ,共72分. 解答应写出文字说明,证明过程或演算步骤.
18、已知数列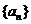 满足
满足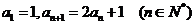 .
.
(1)求证:数列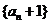 是等比数列;(2)求
是等比数列;(2)求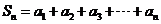 .
.
19、
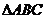 中,
中,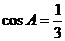 .
.
 (1)求
(1)求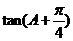 的值; (2)求
的值; (2)求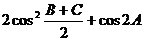 的值.
的值.
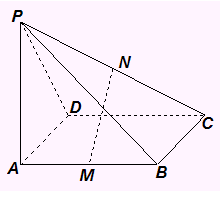
20、四棱锥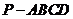 中,
中,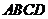 是矩形,
是矩形,
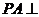 面
面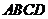 ,
,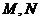 分别是
分别是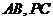 的中点.
的中点.
(1)证明: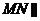 平面
平面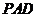 ;
;
(2)若二面角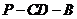 的大小为
的大小为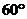 ,
,
求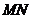 与平面
与平面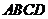 所成的角.
所成的角.
21、已知函数 在区间
在区间 及
及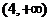 上都是增函数,
上都是增函数,
在区间 上是减函数.
上是减函数.
(1)求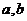 的值;(2)过点
的值;(2)过点 引曲线
引曲线 的切线
的切线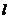 ,求直线
,求直线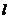 的方程.
的方程.
22、已知曲线
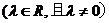 .
.
(1)由曲线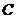 上任一点
上任一点 向
向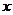 轴作垂线,垂足为
轴作垂线,垂足为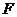 ,点
,点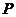 分
分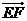 所成的比为
所成的比为 ,
,
问:点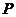 的轨迹可能是圆吗?请说明理由;
的轨迹可能是圆吗?请说明理由;
(2)如果直线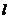 的一个方向向量为
的一个方向向量为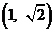 ,且过点
,且过点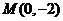 ,直线
,直线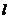 交曲线
交曲线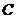 于
于
 、
、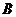 两点,又
两点,又 ,求曲线
,求曲线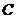 的方程.
的方程.
一、选择题:本大题共10小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
B
D
A
B
B
C
D
二、填空题:本大题7小题,每小题4分,共28分.
11、 ; 12、
; 12、  ; 13、
; 13、 ; 14、
; 14、 ; 15、
; 15、 ; 16、
; 16、 ;17、
;17、 或
或 。
。
三、解答题
18、(1)略 …………………………………………………………………………(7分)
(2) …………………………………………………………(14分)
…………………………………………………………(14分)
19、(1) tanA=
tanA=
 …………………(7分)
…………………(7分)
(2) 原式=
=  ……………………………………………………………………(14分)
……………………………………………………………………(14分)
20、(1)略 ……………………………………………………………………(7分)
(2) 就是二面角
就是二面角 的平面角,即
的平面角,即 ,
,
 …………………………………………………………………(9分)
…………………………………………………………………(9分)
取 中点
中点 ,则
,则 平面
平面 ,
,
 就是
就是 与平面
与平面 所成的角。 …………………………(11分)
所成的角。 …………………………(11分)
 ,
, ,
,
所以 与平面
与平面 所成的角的大小为
所成的角的大小为 。 …………………………(14分)
。 …………………………(14分)
(用向量方法,相应给分)
21、(1) ,
,
又 在区间(-∞,0)及(4,+∞)上都是增函数,在区间(0,4)上是减函数,
在区间(-∞,0)及(4,+∞)上都是增函数,在区间(0,4)上是减函数, 又
又 .………(6分)
.………(6分)
(2)
当点 是切点时,切线方程为9x+6y-16=0.………………(10分)
是切点时,切线方程为9x+6y-16=0.………………(10分)
当点 不是切点时,切点为
不是切点时,切点为 ,
,
得 所以切点为
所以切点为 ,
,
切线方程为 .……………………………………(14分)
.……………………………………(14分)
22、解:解:(1)、设 ,则
,则 ,
,
∵点P分 所成的比为
所成的比为 ∴
∴  ∴
∴ 
∴ 代入
代入 中,得
中,得 为P点的轨迹方程.
为P点的轨迹方程.
当 时,轨迹是圆. …………………………………………………(8分)
时,轨迹是圆. …………………………………………………(8分)
(2)、由题设知直线l的方程为 , 设
, 设
联立方程组 ,消去
,消去 得:
得:
∵ 方程组有两解 ∴  且
且 ∴
∴ 或
或 且
且
∵
 ∴
∴
又 ∵
 ∴
∴  解得
解得 (舍去)或
(舍去)或
∴ 曲线C的方程是 ……………………………………………(16分)
……………………………………………(16分)