河北省唐山市
2006―2007学年度第一学期高三年级期末考试
数学试题(文)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分。考试用时120分钟。
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目用2B铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上。
3.考试结束后,监考人员将本试卷和答题卡一并收回。
参考公式:
如果事件A、B互斥,那么 球的表面积公
P(A+B)=P(A)+P(B)
S=4
如果事件A、B相互独立,那么 其中R表示球的半径
P(A?B)=P(A)?P(B) 球的体积公式
如果事件A在依次实验中发生的概率是 V球=
P,那么n次独立重复实验中恰好发生k 其中R表示球的半径
次的概率

一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求。
1.函数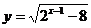 的定义域为 ( )
的定义域为 ( )
A.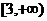 B.
B.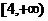
C.(3,+∞) D.(4,+∞)
2.曲线 处的切线在y轴上的截距为 ( )
处的切线在y轴上的截距为 ( )
A.-1 B.-
3.在△ABC中,角A、B、C所对的边分别为a、b、c,已知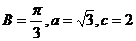 ,则△ABC的面积为 ( )
,则△ABC的面积为 ( )
A.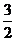 B.
B.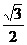 D.
D.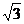
4.函数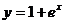 的反函数的图象大致是 ( )
的反函数的图象大致是 ( )
|
 等于 ( )
等于 ( ) B.
B.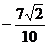 C.
C.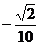 D.
D.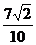
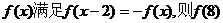 的值 ( )
的值 ( )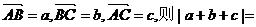 ( )
( )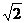 D.
D.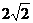
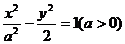 的两条渐近线的夹角为
的两条渐近线的夹角为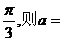 ( )
( )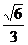 B.
B.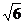 C.
C.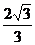 或
或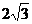
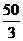 B.
B.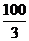 D.16
D.16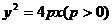 的准线与x轴的交点M作直线l,则“l的斜率等于
的准线与x轴的交点M作直线l,则“l的斜率等于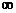 )的函数
)的函数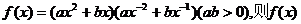 ( )
( )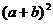 ,没有最小值
,没有最小值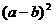
 中,
中,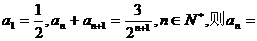 ( )
( ) B.
B.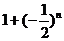 C.
C.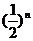 D.
D.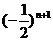
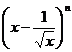 的展开式中二项式系数之和为64,则展开式中常数项是
.
的展开式中二项式系数之和为64,则展开式中常数项是
. 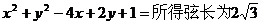 的直线方程为
.
的直线方程为
.  是三个不同的平面,现给出四个命题:
是三个不同的平面,现给出四个命题: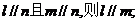 ②若
②若
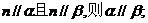 ④若
④若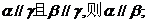
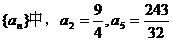
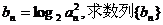 的前n项和Sn.
的前n项和Sn.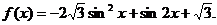
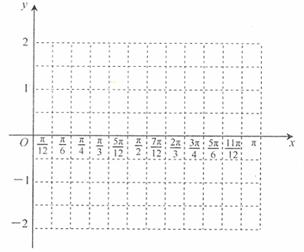
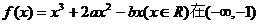 上单调递增,在(-1,2)上单调递减,求实数a的取值范围.
上单调递增,在(-1,2)上单调递减,求实数a的取值范围.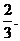
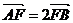 ,求直线AB的斜率k的值.
,求直线AB的斜率k的值.
 …………………………6分
…………………………6分 …………………………12分
…………………………12分 的概率分别为
的概率分别为



 的概率分布为
的概率分布为
 ……………………3分
……………………3分 …………………………6分
…………………………6分 ………………9分
………………9分

 的最小正周期
的最小正周期 ,最小值为-2.…………………………6分
,最小值为-2.…………………………6分








 ,则
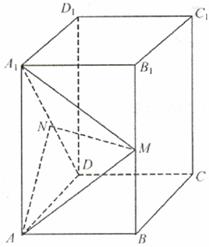
,则 就是所求二面角的平面角.………………………8分
就是所求二面角的平面角.………………………8分
 在△A1OA中由余弦定理得
在△A1OA中由余弦定理得 .
. ……………………………………………12分
……………………………………………12分 .
. .
.
 . ……………………12分
. ……………………12分 …………………………7分
…………………………7分
 …………………………………………12分
…………………………………………12分
 .
. .…………………………………………5分
.…………………………………………5分 得(9+5k2)x2+20kx-25=0,………………………………8分
得(9+5k2)x2+20kx-25=0,………………………………8分 ,
①
,
① .
②
.
② ,
, ,代入①、②得
,代入①、②得 ③
③ ④
④
 …………………………………………14分
…………………………………………14分
 …………………………2分
…………………………2分 ,
,
 单调递增,
单调递增, ,
, ………………………………………………5分
………………………………………………5分 ,
, 单调递增,
单调递增, ,
, …………………………………………8分
…………………………………………8分 ………………………………9分
………………………………9分 ,上式也成立
,上式也成立 ……………11分
……………11分
 ……………………………………………………………………14分
……………………………………………………………………14分