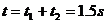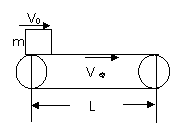1、V₀＝0，（如图1）V₀物体刚置于传送带上时由于受摩擦力作用，将做a =μg的加速运动。假定物体从开始置于传送带上一直加速到离开传送带，则其离开传送带时的速度为V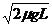＝，显然有：
    V_带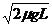＜ 时，物体在传送带上将先加速，后匀速。
    V_带 ≥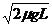时，物体在传送带上将一直加速。
    2、 V₀≠ 0，且V₀与V_带同向，（如图2）

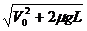（1）V₀＜V_带时同上理可知，物体刚运动到带上时，将做a =μg 的加速运动，假定物体一直加速到离开传送带，则其离开传送带时的速度为V＝ ，显然有：
    V₀＜V_带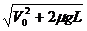＜ 时，物体在传送带上将先加速后匀速。
    V_带 ≥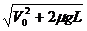 时，物体在传送带上将一直加速。
    （2）V₀＞V_带时
    因V₀＞V_带，物体刚运动到传送带时，将做加速度大小为a = μg的减速运动，假定物体一直减速到离开传送带，则其离开传送带时的速度为V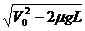＝ ，显然：
    V_带 ≤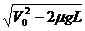时，物体在传送带上将一直减速。
    V₀ ＞V_带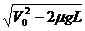＞ 时，物体在传送带上将先减速后匀速。
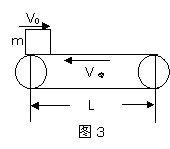
    3、 V₀≠ 0，且V₀与V_带反向，（如图3）

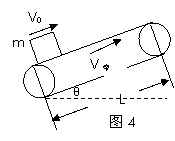
1、V₀＝0，（如图4）
    物体刚放到带的下端时，因V₀＝0，则其受力如图所示，显然只有f - mgsinθ>0，即μ>tgθ时，物体才会被传送带带动从而向上做加速运动，且a=μgcosθ－gsinθ，假定物体一直加速度运动到上端，则物体在离开传送带时的速度为V= 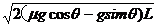，显然：
    V_带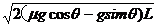＜时，物体在传送带上将先加速后匀速直至从上端离开。
    V_带≥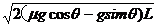时，物体在传送带上将一直加速直至从上端离开。
    2、 V₀≠ 0，且V₀与V带同向，（如图5）

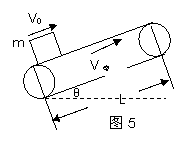
①     V₀＜V_带时，

a、μ>tgθ，物体刚运动到带上时，因V₀<V_带，则其将做a=μgcosθ－gsinθ的加速运动，假定物体一直做加速运动，则物体离开传送带时的速度为V= ，显然：
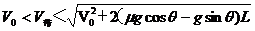 时，物体在传送带上将先加速后匀速直至离开传送带上端。
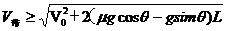    时，物体将在传送带上一直加速直至离开传送带上端。
    b、μ>tgθ 物体刚运动到带上时，因V₀＜V_带，物体将做加速度大小为a＝gsinθ－μgcosθ的减速运动。假定物体一直做减速运动到直至离开传送带，则物体离开传送带上端时速度为V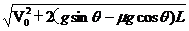＝ ，显然：
    V≥0，即V₀≥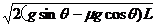时，物体在传送带上将一直减速运动直至从装置的上端离开
    V＜0，即V₀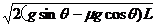＜时，物体在传送带上将先向上做大小为a＝gsinθ－μgcosθ的减速运动，后向下做加速度最小为a＝gsinθ－μgcosθ的加速运动直至离开装置的下端。
    ② V₀＞V_带时
    a、μ>tgθ，物体刚运动到带上时，因V₀＞V_带，故物体将做加速度大小为a＝gsinθ＋μgcosθ的减速运动，假定物体一直做减速运动，则物体离开传送带时速度为V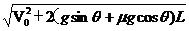＝，显然：
    V_带 ≤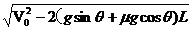时，物体将一直减速直至离开传送带上端。
    V₀＞V_带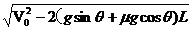＞时，物体将先做减速运动后做匀速运动直至离开传送带上端。
　　b、μ＜tgθ ，物体刚运动到带上时，因V₀＞V_带，故物体将做加速度大小为a＝gsinθ＋μgcosθ的减速运动。假定物体一直做减速运动，则物体离开传送带上端时速度为V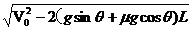＝，显然：
　　V_带 ≤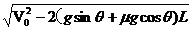时，物体将一直减速直至离开传送带上端。
　　V₀＞V_带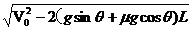＞ 时，，物体运动较为复杂。物体刚开始滑上传送带时，因物体速度大于V带，故物体做a＝gsinθ＋μgcosθ的减速运动，当物体速度减小到等于V_带时，由于继续减速其速度将小于V_带，此后加速大小变为a＝gsinθ－μgcosθ，但是只要其滑上传送带的初速度V₀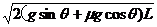＞，就一定能从传送带的上端滑出。
　　若V₀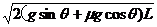＜，则物体有下列两种可能的运动情形。一是先向上做大小为a＝gsinθ＋μgcosθ的减速运动，后向上做大小为a＝gsinθ－μgcosθ的减速运动，直至离开传送带上端。另一种情形是先向上做大小为a＝gsinθ＋μgcosθ的减速运动，再向上做大小为a＝gsinθ－μgcosθ的减速运动，最后向下做为a＝gsinθ－μgcosθ的加速运动直至从下端传送带离开。
　　3、V₀≠ 0，且V₀与V_带反向

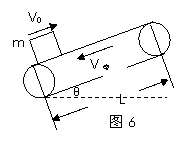
　　物体刚运动到传送带下端时，物体将做加速度大小为a＝gsinθ＋μgcosθ的减速运动，假定物体一直减速，则其离开上端时速度大小为V＝，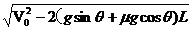
　　显然：
　　当V≥0 ，即V≥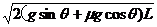时，不论μ为何值，物体将一直减速直至离开传送带上端
　　当V＜0，即V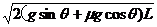＜ 时，则在μ ≥tgθ时，物体将先向上减速后向下匀速直至从下端离开；在μ＜tgθ时，物体将先向上以a＝gsinθ＋μgcosθ做减速运动，后向下做a＝gsinθ－μgcosθ的加速运动直至离开传送带下端。

　　上面我们依据牛顿运动定律对物体在传送带上的运动特征进行了分析，实际上我们还可据能量观点对其进行分析，限于篇幅，本文在这里不再赘述。

2003年高考传送带题

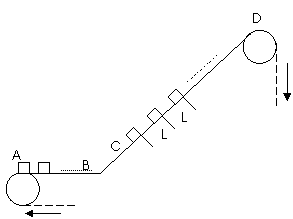一传送带装置示意如图，其中传送带经过AB区域时是水平的，经过BC区域时变为圆孤形（圆孤由光滑模板形成，未画出），经过CD区域时是倾斜的，AB和CD都与BC相切。现将大量的质量均为m的小货箱一个一个在A处放到传送带上，放置时初速为零，经传送带运送到D处，D和A的高度差为h。稳定工作时传送带速度不变，CD段上各箱等距排列，相邻两箱的距离为L。每个箱在A处投放后，在到达B之前已经相对于传送带静止，且以后也不再滑动（忽略经BC段时的微小滑动）。已知在一段相当长的时间T内，共运送小货箱的数目为N。这装置由电动机带动，传送带与轮子间无相对滑动，不计轮轴处的摩擦。求电动机的平均输出功率P.

解：以地面为参考系（下同），设传送带的运动速度为v₀，在水平段运输的过程中，小货箱先在滑动摩擦力作用下做匀加速运动，设这段路程为s，所用时间为t，加速度为a，则对小箱有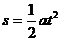① 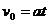   ②  在这段时间内，传送带运动的路程为 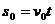③  由以上可得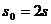④

用f表示小箱与传送带之间的滑动摩擦力，则传送带对小箱做功为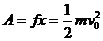⑤

传送带克服小箱对它的摩擦力做功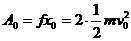⑥

两者之差就是克服摩擦力做功发出的热量 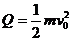  ⑦ 

可见，在小箱加速运动过程中，小箱获得的动能与发热量相等。 T时间内，电动机输出的功为

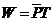 ⑧   此功用于增加小箱的动能、势能以及克服摩擦力发热，即

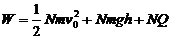  ⑨  已知相邻两小箱的距离为L，所以 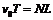⑩

联立⑦⑧⑨⑩，得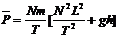 ⑾

平时训练传送带题

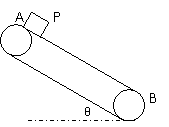
如图所示，倾角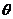=37°的传送带上，上、下两端相距S=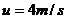7m。当传送带以的恒定速率逆时针转动时，将一个与传送带间动摩擦因数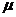=0.25的物块P轻放于A端，P从A端运动到B端所需的时间是多少？若传送带顺时针转动，P从A端运动到B端的时间又是多少？

解答：

当传送带逆时转动时，P下滑的加速度设为a₁，则有

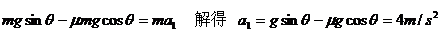
从A 到B的时间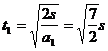当传送带顺时针转动时，设P初始下滑的加速度为a₂，则有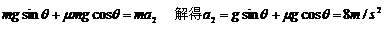

当P加速到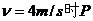对地发生的位移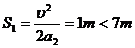

此后P，继续加速下滑，设加速度为，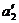

有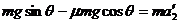所以 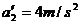滑到B端时的速度

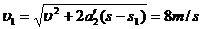
前一段加速滑下时间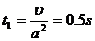后一段加速滑下时间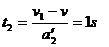

P从A到B总时间