2006――2007学年度第一学期
海口市七年级数学科期终检测题
时间:100分钟 满分:100分 得分:
一、选择题(每小题2分,共20分)
1.计算 -6+4的结果是
A.10
B.
2.下列算式中,结果与34相等的是
A.3+3+3+3 B.4×4×
3.当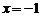 时,代数式
时,代数式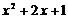 的值是
的值是
A. -2 B.
4. 一个整式减去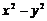 后所得的结果是
后所得的结果是 ,则这个整式是
,则这个整式是
A.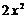 B.
B.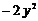 C.
C. D.
D.
5. 由几个大小相同的小正方体积木搭成的立体图形的左视图如图1所示,则所搭成的立体图形不可能是
 |
6. 某人将一枚质量均匀的硬币连续抛10次,落地后正面朝上6次,反面朝上4次,下列说法正确的是
A.出现正面的频率是6 B.出现正面的频率是4
C.出现正面的频率是40% D.出现正面的频率是60%
7.如图2,已知AB⊥CD,垂足为O,图中∠1与∠2的关系是
A.∠1+∠2=90° B.∠1+∠2=180° C.∠1=∠2 D.无法确定
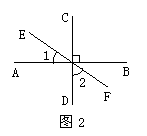
8.下午2点30分时(如图3),时钟的分针与时针所成角的度数为
A.90° B.105° C.120° D.135°
 |
|||||
 |
|||||
 |
|||||
10.一条船停在海面上,从船上看某灯塔位于北偏东30°,那么在这个灯塔上看船应位于
A.南偏东60° B.西偏南40° C.南偏西30° D.北偏东30°
二、填空题(每小题3分,共24分)
11.如果单项式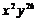 与
与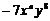 是同类项,则
是同类项,则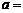 ,
,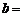 .
.
12. 将多项式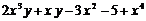 按字母
按字母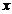 的降幂排列为:
.
的降幂排列为:
.
13. 不改变代数式4x2-2x+y2-4xy+y-3的值, 把二次项放在带有“+”号的括号中,一次项放在带有“-”号的括号中,常数项放在后面. 结果是: +( )-( )-3.
14.用同样规格的黑白两种颜色的正方形瓷砖按图5的方式铺地板,则第3个图案中有白色瓷砖 块,第 个图案中有白色瓷砖
块(用含
个图案中有白色瓷砖
块(用含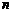 的代数式表示).
的代数式表示).
 |
15.《海口晚报》
16. 图6是《海口晚报》
 |
 17. 如图7,将一副三角板叠放在一起,使直角的顶点重合于点O,并能绕O点自由旋转,若∠DOB=65°,则∠AOC=
°.
17. 如图7,将一副三角板叠放在一起,使直角的顶点重合于点O,并能绕O点自由旋转,若∠DOB=65°,则∠AOC=
°.
 |
18.如图8,D、E、F分别是AB、BC、AC上的点,要使EF∥AB,需添加的一个条件是
(填上你认为适合的一个条件即可).
三、解答题(共56分)
19. (12分)计算
(1)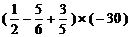 (2)
(2)
20. (7分)先化简,再求值.
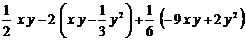 ,其中
,其中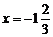 ,
, 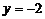 .
.
21.(7分)为方便市民乘车,某市公共汽车公司推出公交IC卡业务,并给予购卡人一定优惠,其中普通卡的优惠方式如下:每购买10元便赠送2元(即卡上金额为12元),第一次购买需交办卡费10元,以后可直接在卡上充值,不另交办卡费.
(1)若某人首次办卡,付款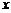 元(
元(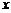 >10), 试用代数式表示卡上显示的金额;
>10), 试用代数式表示卡上显示的金额;
(2)小颖用200元新办了一张普通卡,卡上显示的金额会是多少呢?
22. (10分)利用方格纸画图:
(1)在下边方格纸中,过C点画直线CD∥AB,过C点画直线CE⊥AB于E;
(2)以CF为一边,画正方形CFGH,若每个小格的面积是
(3)在方格纸中有四条直线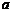 、
、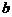 、
、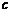 、
、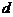 ,其中,能与直线CF平行的是直线 ;能与直线AB垂直的是直线 .
,其中,能与直线CF平行的是直线 ;能与直线AB垂直的是直线 .

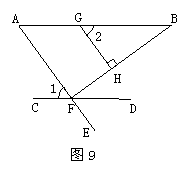 23. (10分) 如图9,AB∥CD,AE交CD于点F,点G在AB上,GH⊥BF,垂足为H,∠1=∠2,直线AE与BF垂直吗?给下面的推理过程填空或填写理由.
23. (10分) 如图9,AB∥CD,AE交CD于点F,点G在AB上,GH⊥BF,垂足为H,∠1=∠2,直线AE与BF垂直吗?给下面的推理过程填空或填写理由.
解:∵ AB∥CD( 已知 ),
∴ ∠1=∠ ( ).
∵ ∠1=∠2,( 已知 ),
∴ ∠ =∠ ( ),
∴ ∥ ( ).
又 ∵ GH⊥BF( ),
∴ ∠AFB=∠GHB=90°( ).
∴ ⊥ .
24. (10分) 表1是第15届多哈亚运会上五个获得金牌总数最多的代表团的奖牌统计表(数据来源:http://www.xinhuanet.com/sports/doha2006/).根据表1中金牌数这一列数据,制成图10.1和10.2的统计图. 利用这些信息,回答下列问题:
表1: 第15届亚运会奖牌榜
国家/地区
金牌
银牌
铜牌
奖牌总数
中国
165
88
63
316
韩国
58
53
82
193
日本
50
71
77
198
哈萨克斯坦
23
19
43
85
泰国
13
15
26
54
其他
119
略
略
略

(1)根据表1,将条形统计图补充完整(用阴影涂黑,标出金牌数);
(2)中国体育健儿在第15届多哈亚运会上共夺得 枚奖牌,其中金牌 枚,约占这届亚运会金牌总数的 %(精确到0.1%),如图10.2,反映在扇形统计图上,这个扇形的圆心角约为 °(精确到度);韩国代表团所获金牌约占这届亚运会金牌总数的 %(精确到0.1%);
(3)简要说明这两幅统计图各有什么特点?
2006―2007学年度第一学期
一、DCCAB DABBC
二、11. 2,4 12. x4+2x3y-3x2+xy-5 13. 4x2+y2-4xy, 2x-y
14. 11,3n+2 15. 2.306×109(或2.306×105万) 16. 107 17. 115
18. 答案不惟一(如∠FEC=∠B,∠DFE+∠FDB=180°…)
三、19.(1)原式=-15+25-18 ………………………………(3分)
=-8 ………………………………(6分)
(2)原式= ………………………………(2分)
………………………………(2分)
=-4-3+1 ………………………………(4分)
=-6 ………………………………(6分)
20.原式 ………………………………(2分)
………………………………(2分)
 ………………………………(4分)
………………………………(4分)
当 ,
, 时,原式
时,原式 ……………(5分)
……………(5分)
=-10+4 ………………………………(6分)
=-6 ………………………………(7分)
21.(1)卡上显示金额为:1.2(x-10)或1.2x-12; …………………………(4分)
(2)当x=2时,1.2(x-10)=(200-10)×1.2-10=228(元).
∴ 卡上显示金额应为228元. ………………(7分)
22.(1)过C点画直线CD∥AB正确. ………………………………(2分)
过C点画直线CE⊥AB于E正确. ………………………………(4分)
(2)画正方形ABCD正确. ………………………………(6分)
正方形ABCD的面积是
(3)d, a ………………………………(10分)
23. ∵ AB∥CD( 已知 ),
∴ ∠1=∠A( 两直线平行,内错角相等 ). ……………………………(2分)
∵ ∠1=∠2( 已知 ),
∴ ∠2=∠A ( 等量代换 ), ………………………………(4分)
∴ AE∥GH( 同位角相等, 两直线平行 ). ………………………………(7分)
又∵ GH⊥BF( 已知 )
∴ ∠AFB=∠GHB=90°,(两直线平行,同位角相等 ) …………………(9分)
∴ AE⊥BF. ………………………………(10分)
24.(1)画图正确. ………………………………(2分)
(2)316, 165, 38.6, 139, 13.6 ( 注:每空1分,共5分) ……(7分)
(3)图10.1, 条形统计图,能清楚地表示每个国家代表队在这届运动会上获得金牌的具体数目. 图10.2, 扇形统计图,能清楚地表示各个国家代表队这届运动会上获得金牌数在总金牌数中所占的百分比. …………………(10分)