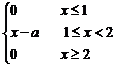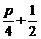2009年高考数学难点突破专题辅导三十
难点30 概 率
概率是高考的重点内容之一，尤其是新增的随机变量这部分内容.要充分注意一些重要概念的实际意义，理解概率处理问题的基本思想方法.
●难点磁场
(★★★★★)如图，用A、B、C三类不同的元件连接成两个系统N1、N2，当元件A、B、C都正常工作时，系统N1正常工作；当元件A正常工作且元件B、C至少有一个正常工作时，系统N2正常工作.已知元件A、B、C正常工作的概率依次为0.80,0.90,0.90，分别求系统N1，N2正常工作的概率P1、P2.
●案例探究
［例1］(★★★★★)有一容量为50的样本，数据的分组及各组的频率数如下：
［10，15］4
［30，35
9 ［15，205 ［35，408 ［20，2510 ［40，453 ［25，3011
(1)列出样本的频率分布表(含累积频率)；
(2)画出频率分布直方图和累积频率的分布图.
命题意图：本题主要考查频率分布表，频率分布直方图和累积频率的分布图的画法.
知识依托：频率、累积频率的概念以及频率分布表、直方图和累积频率分布图的画法.
错解分析：解答本题时，计算容易出现失误，且要注意频率分布与累积频率分布的区别.
技巧与方法：本题关键在于掌握三种表格的区别与联系.
解：(1)由所给数据，计算得如下频率分布表
数据段
［10,15
［15,20
［20,25
［25,30
［30,35
［35,40
［40,45
总计
频数
4
5
10
11
9
8
3
50
频率
0.08
0.10
0.20
0.22
0.18
0.16
0.06
1
累积频率
0.08
0.18
0.38
0.60
0.78
0.94
1
(2)频率分布直方图与累积频率分布图如下：
［例2］(★★★★★)某电器商经过多年的经验发现本店每个月售出的电冰箱的台数ζ是一个随机变量，它的分布列如下：
ζ
1
2
3
……
12
P
……
设每售出一台电冰箱，电器商获利300元，如销售不出而囤积于仓库，则每台每月需花保养费用100元，问电器商每月初购进多少台电冰箱才能使自己月平均收益最大？
命题意图：本题考查利用概率中的某些知识如期望来解决实际问题.
知识依托：期望的概念及函数的有关知识.
错解分析：在本题中，求Ey是一个难点，稍有不慎，就将产生失误.
技巧与方法：可借助概率分布、期望、方差等知识来解决日常生产生活中的实际问题.
解：设x为月初电器商购进的冰箱台数，只须考虑1≤x≤12的情况，设电器商每月的收益为y元，则y是随机变量ζ的函数且y=
,电器商平均每月获益的平均数，即数学期望为：Ey=300x(Px+Px+1+…+P12)+［300－100(x－1)］P1+［2×300－100(x－2)］P2+…+［300(x－1)－100］Px－1
=300x(12－x+1)+ ［300×
］
=
(－2x2+38x)
由于x∈N,故可求出当x=9或x=10时，也即电器商月初购进9台或10台电冰箱时，收益最大.
●锦囊妙记
本章内容分为概率初步和随机变量两部分.第一部分包括等可能事件的概率、互斥事件有一个发生的概率、相互独立事件同时发生的概率和独立重复实验.第二部分包括随机变量、离散型随机变量的期望与方差.
涉及的思维方法：观察与试验、分析与综合、一般化与特殊化.
主要思维形式有：逻辑思维、聚合思维、形象思维和创造性思维.
●歼灭难点训练
一、选择题
1.(★★★★★)甲射击命中目标的概率是
，乙命中目标的概率是
，丙命中目标的概率是
.现在三人同时射击目标，则目标被击中的概率为( )
2.(★★★★)已知随机变量ζ的分布列为：P(ζ=k)=,k=1,2,3,则P(3ζ+5)等于( )
A.6 B.9 C.3 D.4
二、填空题
3.(★★★★)1盒中有9个正品和3个废品，每次取1个产品，取出后不再放回，在取得正品前已取出的废品数ζ的期望Eζ=_________.
4.(★★★★)某班有52人，男女各半，男女各自平均分成两组，从这个班中选出4人参加某项活动，这4人恰好来自不同组别的概率是_________.
三、解答题
5.(★★★★★)甲、乙两人各进行一次射击，如果两人击中目标的概率都是0.6，计算：
(1)两人都击中目标的概率；
(2)其中恰有一人击中目标的概率；
(3)至少有一人击中目标的概率.
6.(★★★★)已知连续型随机变量ζ的概率密度函数f(x)=
(1)求常数a的值，并画出ζ的概率密度曲线；
(2)求P(1＜ζ＜
).
7.(★★★★★)设P在［0,5］上随机地取值，求方程x2+px+
=0有实根的概率.
8.(★★★★★)设一部机器在一天内发生故障的概率为0.2，机器发生故障时全天停止工作.若一周5个工作日里均无故障，可获利润10万元；发生一次故障可获利润5万元，只发生两次故障可获利润0万元，发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少？
难点磁场
解：记元件A、B、C正常工作的事件分别为A、B、C，由已知条件P(A)=0.80, P(B)=0.90,P(C)=0.90.
(1)因为事件A、B、C是相互独立的，所以，系统N1正常工作的概率P1=P(A?B?C)=P(A)P(B)P(C)=0.648,故系统N1正常工作的概率为0.648
(2)系统N2正常工作的概率P2=P(A)?［1－P(
)］
=P(A)?［1－P(
)P(
)］
=0.80×［1－(1－0.90)(1－0.90)］=0.792
故系统N2正常工作的概率为0.792
歼灭难点训练
一、1.解析：设甲命中目标为事件A，乙命中目标为事件B，丙命中目标为事件C，则目标被击中的事件可以表示为A+B+C，即击中目标表示事件A、B、C中至少有一个发生.
故目标被击中的概率为1－P(
??)=1－
答案：A
2.解析：Eξ=(1+2+3)?
=2，Eξ2=(12+22+32)?=
∴Dξ=Eξ2－(Eξ)2=－22=
.
∴D(3ξ+5)=9Eξ=6.
答案：A
二、3.解析：由条件知，ξ的取值为0，1，2，3，并且有P(ξ=0)=
,
答案：0.3
4.解析：因为每组人数为13，因此，每组选1人有C
种方法，所以所求概率为P=
.
答案：
三、5.解：(1)我们把“甲射击一次击中目标”叫做事件A，“乙射击一次击中目标”叫做事件B.显然事件A、B相互独立，所以两人各射击一次都击中目标的概率是P(A?B)?=P(A)?P(B)=0.6×0.6=0.36
答：两人都击中目标的概率是0.36
(2)同理，两人各射击一次，甲击中、乙未击中的概率是P(A?)=P(A)?P()=0.6×
(1－0.6)=0.6×0.4=0.24
甲未击中、乙击中的概率是P(?B)=P()P(B)=0.24，显然，“甲击中、乙未击中”和“甲未击中、乙击中”是不可能同时发生，即事件A?与?B互斥，所以恰有一人击中目标的概率是P(A?)+P(?B)=0.24+0.24=0.48
答：其中恰有一人击中目标的概率是0.48.
(2)两人各射击一次，至少有一人击中目标的概率P=P(A?B)+［P(A?)+P()?B］=0.36+0.48=0.84
答：至少有一人击中目标的概率是0.84.
6.解：(1)因为ξ所在区间上的概率总和为1，所以
(1－a+2－a)?1=1,
∴a=
概率密度曲线如图：
(2)P(1＜ξ＜
)=
7.解：一元二次方程有实数根
Δ≥0
而Δ=P2－4(
)=P2－P－2=(P+1)(P－2)
解得P≤－1或P≥2
故所求概率为P=
8.解：以X表示一周5天内机器发生故障的天数，则X－B(5，0.2)，于是X有概率分布P(X=k)=C
0.2k0.85－k,k=0,1,2,3,4,5.
以Y表示一周内所获利润，则
Y=g(X)=
Y的概率分布为：
P(Y=10)=P(X=0)=0.85=0.328
P(Y=5)=P(X=1)=C
0.2?0.84=0.410
P(Y=0)=P(X=2)=C
?0.22?0.83=0.205
P(Y=－2)=P(X≥3)=1－P(X=0)－P(X=1)－P(X=2)=0.057
故一周内的期望利润为：
EY=10×0.328+5×0.410+0×0.205－2×0.057=5.216(万元)