《空间向量与立体几何》
一、填空题
 1.如图所示,
1.如图所示,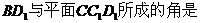 为
为 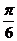 .w.w.w.k.s.5.u.c.o.m
.w.w.w.k.s.5.u.c.o.m
2 【江苏?扬州】4.长方体
【江苏?扬州】4.长方体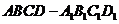 中,
中,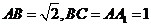 ,则
,则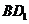 与平面
与平面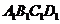
所成的角的大小为 ★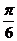 .
.
3.【江苏?苏北四市】10.给出下列关于互不相同的直线m、
l、n和平面α、β的四个命题:
①若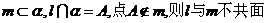 ;
;
②若m、l是异面直线,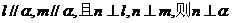 ;
;
③若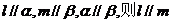 ;
;
 ④若
④若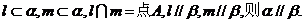
其中为真命题的是▲ ①②④ .
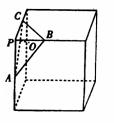 4.【江苏?苏北四市】14.若RtΔABC中两直角边为a、b,斜边c上的高为
4.【江苏?苏北四市】14.若RtΔABC中两直角边为a、b,斜边c上的高为
h,则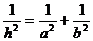 ,如图,在正方体的一角上截取三棱锥P-ABC,PO
,如图,在正方体的一角上截取三棱锥P-ABC,PO
为棱锥的高,记M=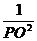 ,N=
,N=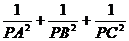 ,那么M、N的大小关系
,那么M、N的大小关系
是▲M=N .
5.【江苏?苏州】已知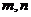 是两条不同的直线,
是两条不同的直线,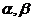 为两个不同的平面,
为两个不同的平面,
有下列四个命题:
①若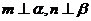 ,m⊥n,则
,m⊥n,则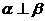 ;
;
②若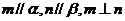 ,则
,则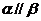 ;
;
③若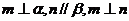 ,则
,则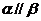 ;
;
④若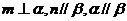 ,则
,则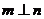 .
.
其中正确的命题是(填上所有正确命题的序号)_______①④________.
6.【江苏?泰州实验】13.已知正四棱锥P―ABCD的高为4,侧棱长与底面所成的角为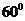 ,则该正四棱锥的侧面积是
,则该正四棱锥的侧面积是 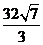 .
.
7.【江苏?泰州】3、已知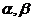 、
、 是三个互不重合的平面,
是三个互不重合的平面,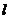 是一条直线,给出下列四个命题:
是一条直线,给出下列四个命题:
①若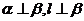 ,则
,则 ;
②若
;
②若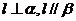 ,则
,则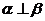 ;
;
③若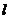 上有两个点到
上有两个点到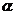 的距离相等,则
的距离相等,则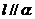 ; ④若
; ④若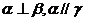 ,则
,则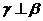 。
。
其中正确命题的序号是 ② ④
8.【江苏?泰州】11、正三棱锥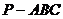 高为2,侧棱与底面成
高为2,侧棱与底面成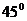 角,则点A到侧面
角,则点A到侧面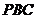 的距离是
的距离是 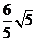
 9.【江苏?盐城】13.如图,在三棱锥
9.【江苏?盐城】13.如图,在三棱锥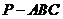 中,
中, 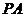 、
、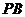 、
、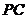 两两垂直,且
两两垂直,且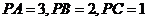 .设
.设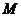 是底面
是底面 内一点,定义
内一点,定义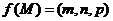 ,其中
,其中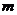 、
、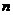 、
、 分别是三棱锥
分别是三棱锥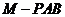 、 三棱锥
、 三棱锥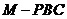 、三棱锥
、三棱锥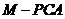 的体积.若
的体积.若 ,且
,且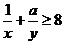 恒成立,则正实数
恒成立,则正实数 的最小值为____▲1____.
的最小值为____▲1____.
二、计算题
1.【江苏?无锡】16.(本小题满分14分)
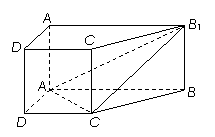 直棱柱
直棱柱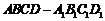 中,底面ABCD是直角梯形,
中,底面ABCD是直角梯形,
∠BAD=∠ADC=90°,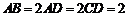 .
.
(Ⅰ)求证:AC⊥平面BB
(Ⅱ)在A1B1上是否存一点P,使得DP与平面BCB1与
平面ACB1都平行?证明你的结论.
证明:(Ⅰ) 直棱柱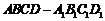 中,BB1⊥平面ABCD,
中,BB1⊥平面ABCD, BB1⊥AC. ………………2分
BB1⊥AC. ………………2分
又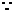 ∠BAD=∠ADC=90°,
∠BAD=∠ADC=90°,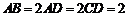 ,
,
∴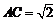 ,∠CAB=45°,∴
,∠CAB=45°,∴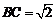 ,
,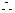 BC⊥AC.………………5分
BC⊥AC.………………5分
又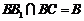 ,
,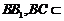 平面BB
平面BB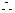 AC⊥平面BB
AC⊥平面BB
(Ⅱ)存在点P,P为A1B1的中点. ……………………………………8分
证明:由P为A1B1的中点,有PB1‖AB,且PB1=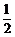 AB.……………………9分
AB.……………………9分
又∵DC‖AB,DC=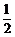 AB,
AB,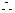 DC ∥PB1,且DC= PB1,
DC ∥PB1,且DC= PB1,
∴DC PB1为平行四边形,从而CB1∥DP.…………………………11分
又CB1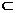 面ACB1,DP
面ACB1,DP  面ACB1,
面ACB1, DP‖面ACB1.………………………………13分
DP‖面ACB1.………………………………13分
同理,DP‖面BCB1.…………………………………………………14分
评讲建议:
本题主要考查线面平行、垂直的的判定和证明等相关知识,第一小题要引导学生挖掘直角梯形ABCD中BC⊥AC,第二小题,要求学生熟练掌握一个常用结论:若一直线与两相交平面相交,则这条直线一定与这两平面的交线平行;同时注意问题的逻辑要求和答题的规范性,这里只需要指出结论并验证其充分性即可,当然亦可以先探求结论,再证明之,这事实上证明了结论是充分且必要的.
2.【江苏?淮、徐、宿、连】16.(本小题满分14分)
如图,四边形ABCD为矩形,BC上平面ABE,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;
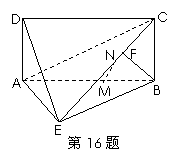 (2)设点M为线段AB的中点,点N为线段CE的中点.
(2)设点M为线段AB的中点,点N为线段CE的中点.
求证:MN∥平面DAE.

【解】(1)证明:因为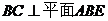 ,
,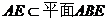 ,
,
所以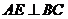 ,………………………………………………2分
,………………………………………………2分
又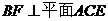 ,
,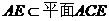 ,
,
 所以
所以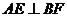 , ……………………………………………4分
, ……………………………………………4分
又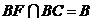 ,所以
,所以 ……………………………………………6分
……………………………………………6分
又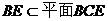 ,所以
,所以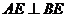 .……………………………………………8分
.……………………………………………8分
(2)取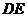 的中点
的中点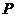 ,连接
,连接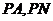 ,因为点
,因为点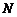 为线段
为线段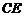 的中点.
的中点.
所以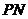 ||
||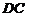 ,且
,且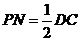 , ……………………………………………………10分
, ……………………………………………………10分
又四边形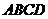 是矩形,点
是矩形,点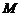 为线段
为线段 的中点,所以
的中点,所以 ||
||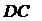 ,且
,且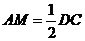 ,
,
所以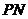 ||
||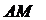 ,且
,且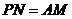 ,故四边形
,故四边形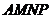 是平行四边形,所以
是平行四边形,所以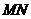 ||
||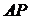 …………12分
…………12分
而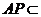 平面
平面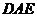 ,
,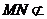 平面
平面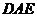 ,所以
,所以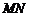 ∥平面
∥平面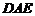 . …………………14分
. …………………14分
3.
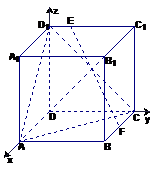
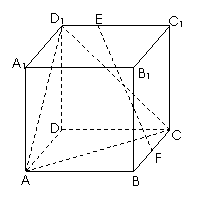 【江苏?淮、徐、宿、连】22.在正方体ABCD―A1B
【江苏?淮、徐、宿、连】22.在正方体ABCD―A1B
F是BC的中点,点E在D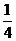 D
D
EF与平面D
【解】设正方体棱长为1,以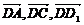 为单位正交基
为单位正交基
底,建立如图所示坐标系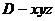 ,则各点的坐标分别为
,则各点的坐标分别为
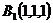 ,
,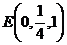 ,
, 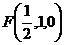 ,……………………2分
,……………………2分
 所以
所以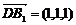 ,
,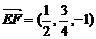 , ……………………4分
, ……………………4分
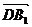 为平面
为平面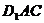 的法向量,
的法向量,
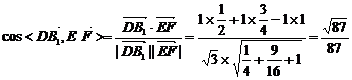 .……8分
.……8分
所以直线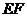 与平面
与平面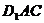 所成角的正弦值为
所成角的正弦值为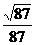 .………………………………10分
.………………………………10分
4.【江苏?南通】15.(本小题14分)
如图,在正三棱柱ABC-A1B
 (1)求证:AD⊥平面BC C1 B1;
(1)求证:AD⊥平面BC C1 B1;
(2)设E是B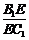 的值为多少时,
的值为多少时,
A1E∥平面ADC1?请给出证明.
解: (1)在正三棱柱中,C C1⊥平面ABC,AD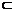 平面ABC,
平面ABC,
∴ AD⊥C C1.………………………2分
又AD⊥C1D,C C1交C1D于C1,且C C1和C1D都在面BC C1 B1内,
∴ AD⊥面BC C1 B1. ……………………………………………5分
(2)由(1),得AD⊥BC.在正三角形ABC中,D是BC的中点.…………7分
当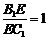 ,即E为B
,即E为B
事实上,正三棱柱ABC-A1B
又B1B∥AA1,且B1B=AA1,
∴DE∥AA1,且DE=AA1. …………………………………………12分
所以四边形ADE A1为平行四边形,所以E A1∥AD.
而E A1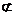 面AD C1内,故A1E∥平面AD C1. …………………………14分
面AD C1内,故A1E∥平面AD C1. …………………………14分
5.【江苏?启东中学模拟】
|

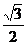 ,D为AB的中点.
,D为AB的中点.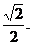
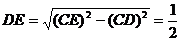 ;
;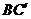 ,证明:
,证明: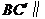 面
面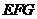 .
.

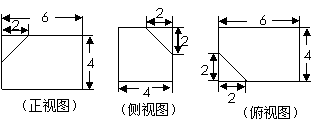
 ------------4分
------------4分 (2)所求多面体体积
(2)所求多面体体积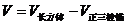
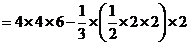
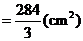 .--------9分
.--------9分 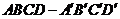 中,
中,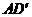 ,则
,则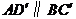 .
.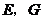 分别为
分别为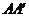 ,
,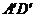 中点,所以
中点,所以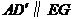 --11分
--11分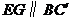 .又
.又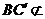 平面
平面 16. (本题满分14分)
16. (本题满分14分) 中,
中,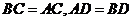 ,
,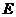 是
是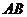 的中点.
的中点.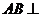 平面CDE;
平面CDE;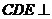 平面
平面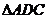 的重心,试在线段AE上确定一点F,使得GF
的重心,试在线段AE上确定一点F,使得GF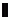 平面CDE.
平面CDE.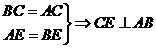 同理,
同理,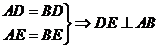
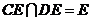 ∴
∴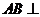 平面
平面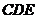 . …………………5分
. …………………5分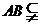 平面
平面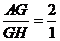 ,
,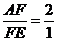 ,则
,则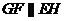 ,易知GF
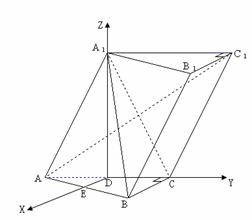
,易知GF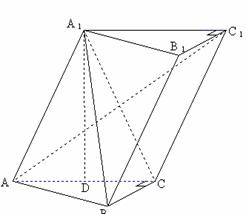 4. 已知斜三棱柱
4. 已知斜三棱柱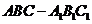 ,
,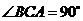 ,
,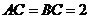 ,
,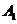 在底面
在底面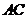 的中点
的中点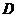 ,又知
,又知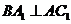 。
。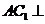 平面
平面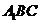 ;
;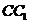 到平面
到平面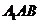 的距离;
的距离;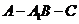 余弦值的大小。
余弦值的大小。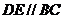 ,因为
,因为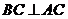 ,
, 所以
所以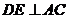 ,又
,又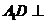 平面
平面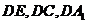 为
为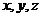 轴建立空间坐标系,
轴建立空间坐标系,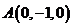 ,
, ,
,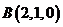 ,
,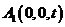 ,
, ,
,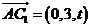 ,
,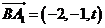 ,
,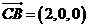 ,由
,由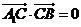 ,知
,知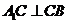 ,
,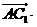
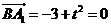 ,得
,得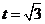 。
。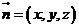 ,
,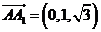 ,
,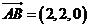 ,所以
,所以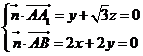 ,设
,设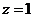 ,则
,则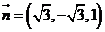
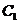 到平面
到平面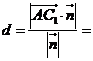
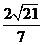 。
。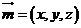 ,
,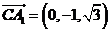 ,
,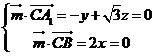 ,设
,设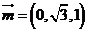 ,
,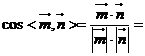
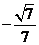 ,根据法向量的方向,
,根据法向量的方向,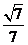
 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.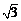 ,AC=2.
,AC=2.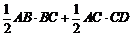
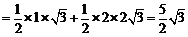 .……………… 3分
.……………… 3分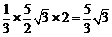 . ……………… 5分
. ……………… 5分 (Ⅱ)∵PA=CA,F为PC的中点,
(Ⅱ)∵PA=CA,F为PC的中点, 平面PAB,PA
平面PAB,PA 平面PAB,
平面PAB, ∵MC
∵MC 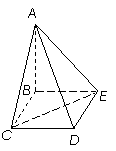 16. (本题满分14分)四棱锥
16. (本题满分14分)四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面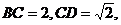
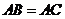 .
.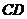 的中点为
的中点为 ,
,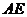 的中点为
的中点为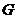 ,证明:
,证明: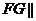 面
面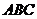 ;
;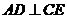 .
. 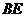 的中点为
的中点为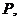 连
连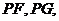 可以证明
可以证明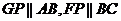
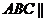 面
面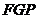 ,
, 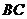 中点
中点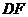 交
交 于点
于点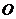 ,
,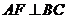 ,
,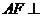 面
面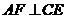 .………………….10分
.………………….10分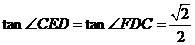 ,
,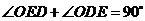 ,
,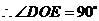 ,即
,即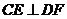 ,
,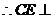 面
面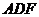 ,
,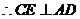 .………………….14分
.………………….14分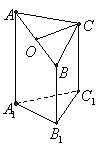 右图是一个直三棱柱(以
右图是一个直三棱柱(以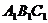 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为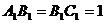 ,
,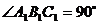 ,
,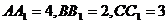 .
.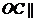 平面
平面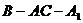 的大小;
的大小;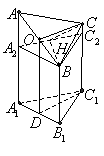 (1)证明:作
(1)证明:作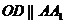 交
交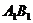 于
于 .
.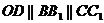 .
.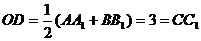 .
.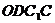 是平行四边形,因此有
是平行四边形,因此有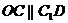 .
. 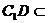 平面
平面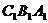 且
且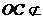 平面
平面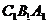 ,
,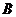 作截面
作截面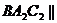 面
面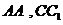 于
于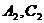 .
. 于
于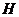 ,连
,连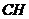 .
.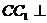 面
面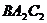 ,所以
,所以 ,则
,则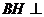 平面
平面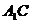 .
.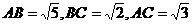
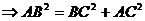 .
.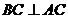 ,根据三垂线定理知
,根据三垂线定理知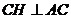 ,所以
,所以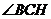 就是所求二面角的平面角.
就是所求二面角的平面角. ,所以
,所以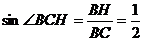 ,故
,故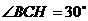 ,
,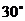 .……………….10分
.……………….10分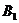 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,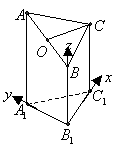 则
则 因为
因为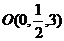 ,
,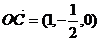 .
. 是平面
是平面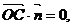
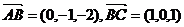 ,
,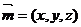 是平面
是平面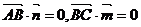 得:
得: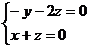
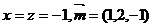 .
.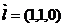 为平面
为平面 的一个法向量.
的一个法向量.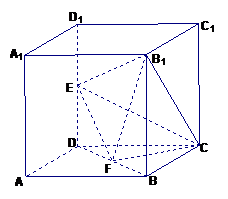 则
则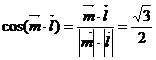 ,结合图形可知所求二面角为锐角.
,结合图形可知所求二面角为锐角. 、
、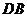 的
的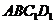 ;
;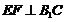 ;
;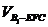 的体积.
的体积.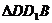 中,
中,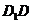 ,
,
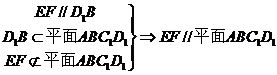
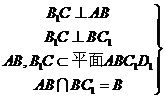
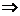
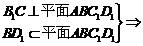
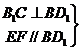
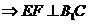
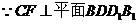
 且
且 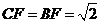
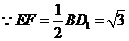 ,
,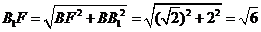
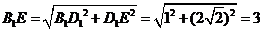
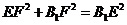 即
即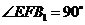
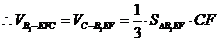 =
=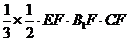
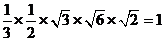
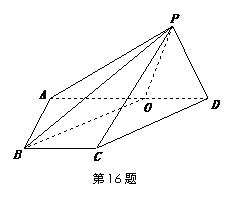 如图,在四棱锥
如图,在四棱锥 中,侧面
中,侧面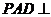 底面
底面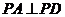 ,底面
,底面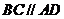 ,
,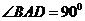 ,
,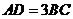 ,
,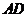 上一点.
上一点.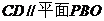 ,试指出点
,试指出点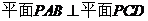 .
. 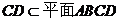 ,且
,且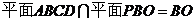 ,
,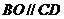 ………………………………………………………(4分)
………………………………………………………(4分)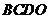 为平行四边形,则
为平行四边形,则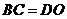 ……………………………………(6分)
……………………………………(6分)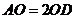 …………………………………………………(7分)
…………………………………………………(7分)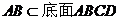 ,且
,且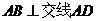 ,
,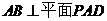 ,则
,则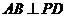 ………………………………………(10分)
………………………………………(10分)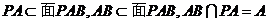 ,所以
,所以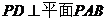 ………(13分)
………(13分) ,所以
,所以
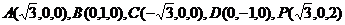 ,
,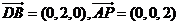 …(2分)
…(2分)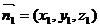 ,
,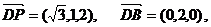
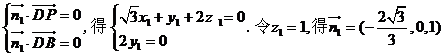 ,
,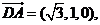
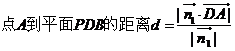 =
= ………………………………(5分)
………………………………(5分)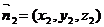 ,
,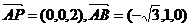 ,
,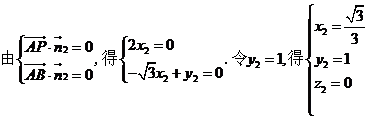 ,
,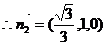 ,
,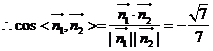 ,而所求的二面角与
,而所求的二面角与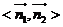 互补,
互补,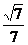 ………………………………………(10分)
………………………………………(10分)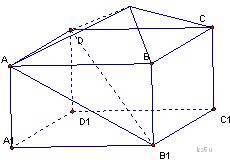
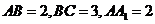 ,点
,点 平面
平面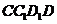 且
且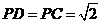
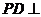 平面
平面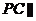 平面
平面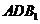 。
。