1.在直角坐标系中，若一点的纵、横坐标都是整数，则称该点为整点.设k为整数，当直线y=x-2与y=kx+k的交点为整点时，k的值可以取(　)

　　(A)4个　　　　(B)5个　　　　(C)6个　　　　　(D)7个

2.如图，AB是⊙O的直径，C为AB上的一个动点(C点不与A、B重合)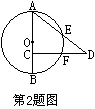，CD⊥AB，AD、CD分别交⊙O于E、F，则与AB?AC相等的一定是(　)

　(A)AE?AD　　 (B)AE?ED　　 (C)CF?CD　　 (D)CF?FD

3.在△ABC与△A′B′C′中，已知AB＜A′B′，BC＜B′C′，CA＜C′A′.下列结论：

　　(1)△ABC的边AB上的高小于△A′B′C′的边A′B′上的高；

　　(2)△ABC的面积小于△A′B′C′的面积；

　　(3)△ABC的外接圆半径小于△A′B′C′的外接圆半径；

　　(4)△ABC的内切圆半径小于△A′B′C′的内切圆半径.

　　其中，正确结论的个数为(　)

　　(A)0　　　　　(B)1　　　　　　(C)2　　　　　(D) 4

4.设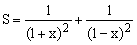，那么S与2的大小关系是(　)

　　(A)S=2　　　　　　　　　(B)S＜2

　　(C)S＞2　　　　　 　　　(D)S与2之间的大小与x的取值有关

5.折叠圆心为O、半径为10cm的圆纸片，使圆周上的某一点A与圆心O重合.对圆周上的每一点，都这样折叠纸片，从而都有一条折痕.那么，所有折痕所在直线上点的全体为(　)

(A)以O为圆心、半径为10cm的圆周

　(B)以O为圆心、半径为5cm的圆周

　(C)以O为圆心、半径为5cm的圆内部分　

(D)以O为圆心，半径为5cm的圆周及圆外部分

6.已知x，y，z都是实数，且x²+y²+z²=1，则m=xy+yz+zx(　)

　　(A)只有最大值　　　　　　　　　(B)只有最小值

　　(C)既有最大值又有最小值　　　　 (D)既无最大值又无最小值

　7.如图是一个树形图的生长过程，依据图中所示的生长规律，第15行的实心圆点的个数等于______.

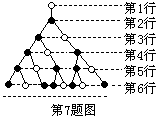
　8.设0.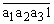为四位十进制纯小数，a_i(i=1,2,3)只取0或1.记T是所有这些四位小数的个数 ，S是所有这些四位小数的和，则=______.

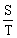　9.如图，取一张长方形纸片，它的长AB=10cm，宽BC=5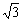cm，然后以虚线CE(E点在AD上)为折痕，使D点落在AB边上.则AE=_____cm，∠DCE=______°.

10.直角三角形ABC中，∠A=90°，AB=5cm，AC=4cm，则∠A的平分线AD的长为______cm.

　11.房间里有凳子(3条腿)、椅子(4条腿)若干张，每张凳子或椅子只能坐1人.一些人进来开会，只坐凳子或只坐椅子都不够坐，但每人都有椅子或凳子坐，且还有空位，已知人腿、凳腿、椅腿之和为32，则房间里共有______个人、______张凳子、______张椅子.

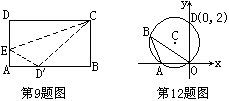
12.如图，⊙C通过原点，并与坐标轴分别交于A，D两点.已知∠OBA=30°，点D的坐标为(0,2)，则点A，C的坐标分别为A(　,　)；C(　,　).

　13.若关于x的方程rx²-(2r+7)x+(r+7)=0的根是正整数，则整数r的值可以是______.

　14.将2,3,4,5,…,n(n为大于4的整数)分成两组，使得每组中任意两数之和都不是完全平方数.那么，整数n可以取得的最大值是______.

15.初三(8)班尚剩班费m(m为小于400的整数)元，拟为每位同学买1本相册.某批发兼零售文具店规定：购相册50本起可按批发价出售，少于50本则按零售价出售，批发价比零售价每本便宜2元，班长若为每位同学买1本，刚好用完m元；但若多买12本给任课教师，可按批发价结算，也恰好只要m元.问该班有多少名同学？每本相册的零售价是多少元？

16.已知关于x的方程x²+4x+3k-1=0的两个实根的平方和不小于这两个根的积；反比例函数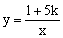的图像的两个分支在各自的象限内，点的纵坐标y随点的横坐标x的增大而减小.求满足上述条件的k的整数值.

17.求360的所有正约数的倒数和.

18.如图，在△ABC中，BC=6，AC=4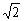，∠C=45°，P为BC上的动点，过P作PD∥AB交AC于点D，连结AP，△ABP、△APD、△CDP的面积分别记为S₁，S₂，S₃，设BP=x.

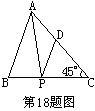
　　(1)试用x的代数式分别表示S₁，S₂，S₃；

　　(2)当P点位于BC上某处使得△APD的面积最大时，你能得出S₁、S₂、S₃之间或S₁、S₂、S₃两两之间的哪些数量关系(要求写出不少于3条)？