 重庆江津市高2007级四校联考
重庆江津市高2007级四校联考
数学试卷(文科)
(五中、六中、几江、八中)命题:刘家财 审核:章元良
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.全卷共三个大题,22个小题,满分150分,考试时间为120分钟.
注意事项:
1.答卷前,考生务必将自己的学校、班级、姓名、考号填写在答题卡上.
2.第I卷每小题选出答案后,用笔填写在答题卡上“第I卷答题栏”对应题目的答案栏内.不能答在试题纸上.
3.第II卷各题一定要做在答题卡限定的区域内.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设全集U={1,2,3,4,5}, 若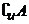 ={1,4},
={1,4}, 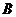 ={1,2} , 则
={1,2} , 则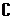 U(A∪B) ( )
U(A∪B) ( )
A.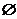 B.{1,3,4,5} C.{1,2,3,4,5} D.{4}
B.{1,3,4,5} C.{1,2,3,4,5} D.{4}
2.函数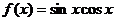 是 ( )
是 ( )
A.周期为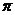 的奇函数 B.周期为
的奇函数 B.周期为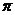 的偶函数
的偶函数
C.周期为2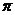 的奇函数 D.周期为2
的奇函数 D.周期为2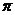 的偶函数
的偶函数
3.已知向量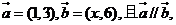 则x的值为( )
则x的值为( )
A.1 B.
4.等差数列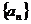 中,
中,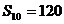 ,那么
,那么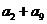 的值是:( )
的值是:( )
A. 12 B.
5. 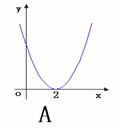 函数f(x)=
函数f(x)=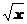 +2(x
+2(x 0)的反函数f
0)的反函数f (x)的图象是 ( )
(x)的图象是 ( )
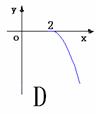
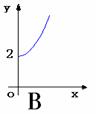
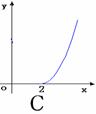
6.下列命题中,假命题为 --------------------------------------------------( )
A.若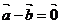 ,则
,则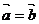 B.若
B.若 ,则
,则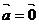 或
或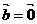
C.若k∈R,k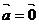 ,则k=0或
,则k=0或 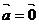 D.若
D.若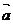 ,
,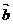 都是单位向量,则
都是单位向量,则 ≤1恒成立
≤1恒成立
7.设命题甲: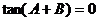 ;命题乙:
;命题乙: ;则甲是乙的( )条件
;则甲是乙的( )条件
A. 充要 B. 充分不必要 C. 必要不充分 D.既不充分也不必要
8.在区间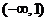 上递增的函数是
上递增的函数是
A.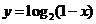 B.
B. 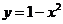 C.
C.  D .
D .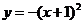
9.已知圆O的方程为x2+y2=r2,点P(a,b)(ab≠0)是圆O内一点,以P为中点的弦所在的直线为m,直线n的方程为ax+by=r2,则 ( )
A.m∥n,且n与圆O相交 B.m∥n,且n与圆O相离
C.m与n重合,且n与圆O相离 D.m⊥n,且n与圆O相离
10.设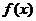 是定义在R上的奇函数,若当
是定义在R上的奇函数,若当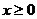 时,
时,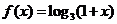 ,则
,则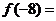
A.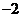 B.
B.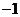 C.
C.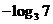 D.
D.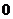
11.如图,把椭圆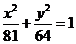 的长轴
的长轴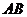 分成
分成 等份,过每个分点作
等份,过每个分点作 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于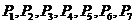 七个点,
七个点,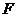 是椭圆的一个焦点,
是椭圆的一个焦点,
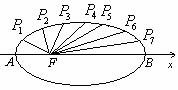 则
则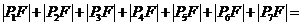 ( )
( )
A. 63 B.
12.一机器狗每秒钟前进或后退一步,程序设计师让机器狗以前进3步,再后退2步的规律移动,如果将此机器狗放在数轴的原点,面向正方向,以一步的距离为一个单位长,令P(n)表示第n秒时机器狗所在位置的坐标,且P(0)=0,那么下列结论中错误的是 ( )
A、P(3)=3 B、P(99)= P(109)
P(109)
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分,把答案填写在答题卡的相应位置)
13.在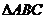 中,如果
中,如果 ,那么角C= ..
,那么角C= ..
14.在条件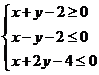 下,则
下,则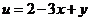 的最大值是
.
的最大值是
.
15.对任意的 .
.
16.对于给定的函数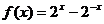 ,有下列结论:
,有下列结论:
①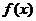 的图象关于原点对称; ②
的图象关于原点对称; ②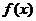 是R上的增函数
是R上的增函数
③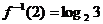 ④
④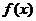 有最小值0
有最小值0
其中正确命题的序号是 .
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分13分)已知函数
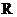 ,
,
求(1)函数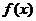 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量 的集合;
的集合;
(2)函数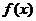 的单调增区间.
的单调增区间.
18.(本小题满分13分)已知函数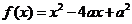
(1)若关于 的不等式
的不等式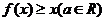 的解集为R,求实数
的解集为R,求实数 的取值范围;
的取值范围;
(2)若函数 ,且函数
,且函数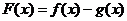
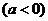 在
在 的最小值为4,求
的最小值为4,求 的值
的值
19.(本小题满分12分)已知向量
且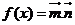 ,解关于x的不等式f(x)
< 0的解集
,解关于x的不等式f(x)
< 0的解集
20.(本小题满分12分) 
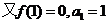
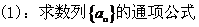
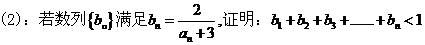
21.(本小题满分12分)
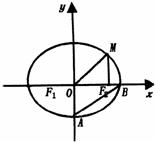
如图,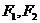 分别是椭圆
分别是椭圆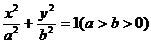 的左右焦点,M为椭圆上一点,
的左右焦点,M为椭圆上一点,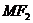 垂直于
垂直于 轴,且OM与椭圆长轴和短轴端点的连线AB平行,
轴,且OM与椭圆长轴和短轴端点的连线AB平行,
(Ⅰ)求椭圆的离心率;
(II)过 且与OM垂直的直线交椭圆于P,Q.若
且与OM垂直的直线交椭圆于P,Q.若 ,求椭圆的方程.
,求椭圆的方程.
22(本小题满分12分)定义在R上的函数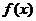 满足
满足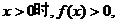 且对任意
且对任意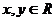 ,都有
,都有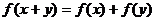 。
。
(1)求证: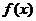 为奇函数;
为奇函数;
(2)求证: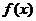 为增函数
为增函数
(3)若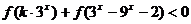 对任意
对任意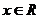 恒成立,求实数
恒成立,求实数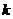 的取值范围
的取值范围
重庆江津市高2007级四校联考
Ⅰ 选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
A
B
C
C
B
C
C
B
A
A
B
Ⅱ 非选择题
二、13. 14.4 15.-2
16.① ②
14.4 15.-2
16.① ②
三、解答题:
17.(I)解:

 --------------------------4分
--------------------------4分
 当
当 ,即
,即 时,
时, 取得最大值
取得最大值 .
.
因此, 取得最大值的自变量x的集合是
取得最大值的自变量x的集合是 -------8分
-------8分
(Ⅱ)解:
由题意得 ,即
,即 .
.
因此, 的单调增区间是
的单调增区间是 .-------------------13分
.-------------------13分
18.⑴∵f (x) ≥x的解集为R
∴x2-(
∴△=(
即
(
∴? ≤a≤?
≤a≤?
∴a的取值范围为[? ,?
,? ]
------------------------------------------------------6分
]
------------------------------------------------------6分
(2)∵ ,---------------------------------------------------------8分
,---------------------------------------------------------8分
由 的对称轴
的对称轴 ,知
,知 在
在 单调递增
单调递增
∴ 在
在 处取得最小值,即
处取得最小值,即 ---------------------------------------------------11分
---------------------------------------------------11分
∴ 解得
解得 或
或 ∵
∵ ∴
∴ ----------------------13分
----------------------13分
19、解:由 <0,得
<0,得
即 (*)----------------------------------------------------------------------2分
(*)----------------------------------------------------------------------2分
⑴当 a>0时,(*)等价于 <
< a
a
∴不等式的解为: <x<1--------------------------------------------------------------------5分
<x<1--------------------------------------------------------------------5分
⑵当a=0时,(*)等价于 <0即x<1----------------------------------------------------8分
<0即x<1----------------------------------------------------8分
⑶当a<0时,(*)等价于 >
> a
a
∴ 不等式的解为 : x<1或x> -----------------------------------------------------11分
-----------------------------------------------------11分
综上所述:当a>0时,不等式的解集为( ,1);当a=0时,不等式的解集为
,1);当a=0时,不等式的解集为 ;
;
当a<0时,不等式的解集为 ∪(
∪( ,
, )-------------------------------12分
)-------------------------------12分
20.



 ---------------------------------------------------------------------------------3分
---------------------------------------------------------------------------------3分


 ---------------------------------------------------------------------7分
---------------------------------------------------------------------7分

 ---------------------------------12分
---------------------------------12分
21.解:(1)由已知


 ,
,
(2)




 椭圆的方程为
椭圆的方程为
22.(1)证明:f(x+y)=f(x)+f(y)(x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,则有0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,所以f(x)是奇函数.---------------------------------------3分
(2)设 则
则

所以f(x)是增函数.----------------------------------------------------6分
(3)解:∵由(2)知f(x) 在R上是单调增函数,又由(1)f(x)是奇函数.
f(k?3 )<-f(3
)<-f(3 -9
-9 -2)=f(-3
-2)=f(-3 +9
+9 +2), k?3
+2), k?3 <-3
<-3 +9
+9 +2,
+2,
3 -(1+k)?3
-(1+k)?3 +2>0对任意x∈R成立.
+2>0对任意x∈R成立.
令t=3 >0,问题等价于t
>0,问题等价于t -(1+k)t+2>0对任意t>0恒成立.
-(1+k)t+2>0对任意t>0恒成立.




 R恒成立.
R恒成立.
---------------------------------------------------------------------------12分