07届广东省仲元中学数学选择填空题专项训练(1)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的
1、函数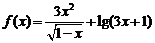 的定义域是
的定义域是
A.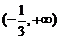 B.
B.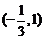 C.
C.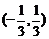 D.
D.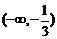
2、若复数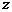 满足方程
满足方程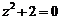 ,则
,则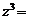
A.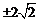 B.
B.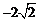 C.
C.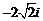 D.
D.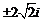
3、下列函数中,在其定义域内既是奇函数又是减函数的是
A.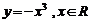 B.
B.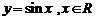
C.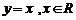 D.
D.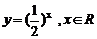
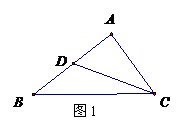 4、如图1所示,
4、如图1所示,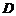 是
是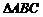 的边
的边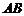 上的中点,则向量
上的中点,则向量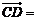
A.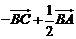
B.
C.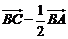
D.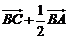
5、给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面
③如果两条直线都平行于一个平面,那么这两条直线互相平行
④如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
其中真命题的个数是
A.4
B.
6、已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为
A.5
B.
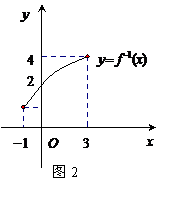 7、函数
7、函数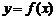 的反函数
的反函数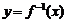 的图像与
的图像与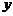 轴交于点
轴交于点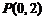 (如图2所示),则方程
(如图2所示),则方程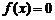 在
在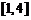 上的根是
上的根是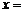
A.4
B.3
C.2
D.1
8、已知双曲线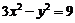 ,则双曲线右支上的点
,则双曲线右支上的点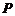 到右焦点的距离与点
到右焦点的距离与点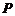 到右准线的距离之比等于
到右准线的距离之比等于
A.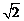 B.
B.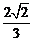 C.2
D.4
C.2
D.4
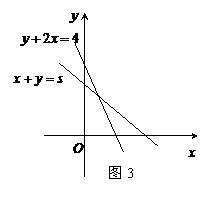 9、在约束条件
9、在约束条件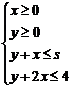 下,当
下,当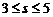 时,目标函数
时,目标函数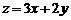 的最大值的变化范围是
的最大值的变化范围是
A.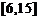
B.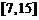
C.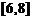
D.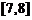
10、对于任意的两个实数对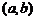 和
和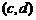 ,规定:
,规定: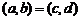 ,当且仅当
,当且仅当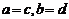 ;运算“
;运算“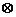 ”为:
”为: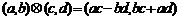 ;运算“
;运算“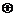 ”为:
”为: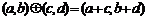 ,设
,设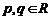 ,若
,若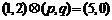 ,则
,则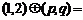
A.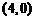 B.
B.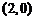 C.
C.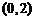 D.
D.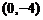
二、填空题:本大题共4小题,每题5分,共20分.
11、棱长为3的正方体的顶点都在同一球面上,则该球的表面积为______.
12、在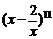 的展开式中,
的展开式中,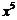 的系数为________.
的系数为________.
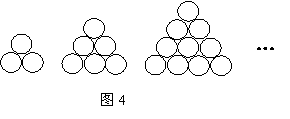 13、在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第
13、在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第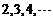 堆最底层(第一层)分别按图4所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第
堆最底层(第一层)分别按图4所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第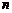 堆第
堆第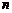 层就放一个乒乓球,以
层就放一个乒乓球,以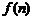 表示第
表示第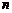 堆的乒乓球总数,则
堆的乒乓球总数,则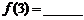 ;
;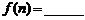 (答案用
(答案用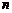 表示).
表示).
三.解答题
14、(本题14分)
已知函数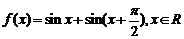 .
.
(1)求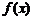 的最小正周期;
的最小正周期;
(2)求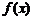 的的最大值和最小值;
的的最大值和最小值;
(3)若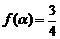 ,求
,求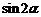 的值.
的值.
1-10 BDAAB CCCDB
二、填空题
11、
12、 ,所以
,所以 的系数为
的系数为
13、 10,
10,
三、解答题
14、
(1) 的最小正周期为
的最小正周期为 ;
;
(2) 的最大值为
的最大值为 和最小值
和最小值 ;
;
(3)因为 ,即
,即 ,即
,即 