如何应用讨论法解题
文／杨基鄂
??一、讨论法的涵义
??讨论法是化学计算中的一种常用方法。这种方法多用于计算题在缺乏条件，求解时一个方程中出现几个未知数以及一些用字母表示的过量计算，不能得到定解时需要在分析推理的基础上通过某些假设条件，加以讨论才有定解。
??二、讨论法解题的一般思路
??用讨论法解计算题，先要分析条件与求解问题之间的联系，建立讨论模型，然后形成解题的方法。如列出二元一次方程或写出并列的各个化学方程式（或离子方程式）等，按顺序分析排查，确定答案。现举例加以说明。
??三、讨论法的解题方法
??例1.某金属氧化物的式量为Ｍ，该金属同种价态的氯化物的式量为Ｎ，则该金属元素的化合价为（ ）。
??Ａ．（2Ｎ－Ｍ）／55 Ｂ.［2（Ｎ－Ｍ）］／55
??Ｃ.（2Ｍ－Ｎ）／55 Ｄ.［2（Ｍ－Ｎ）］／55
??解：设该金属相对原子质量为A，化合价为ｘ。
??（1）当ｘ为奇数时，有Ｒ2Ｏｘ，ＲＣｌｘ。
则有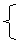
2ａ＋16ｘ＝Ｍ
①
ａ＋35．5ｘ＝Ｎ
②
??解得?55ｘ＝2Ｎ－Ｍ，
ｘ＝（2Ｎ－Ｍ）／55
??（2）当ｘ为偶数时，有ＲＯ（ｘ／2），ＲＣｌｘ。
则有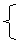
ａ＋8ｘ＝Ｍ
①
ａ＋35．5ｘ＝Ｎ
②
??解得 27．5ｘ＝Ｎ－Ｍ
??ｘ＝（Ｎ－Ｍ）／27．5＝［2（Ｎ－Ｍ）］／55
??故选A、B。
??例2.已知2Ａ＋3Ｂ＝6Ｃ＋Ｄ式中A是含Ｘ、Ｙ两种元素的化合物，B是只含Z元素的单质，C和D均是双原子分子。试确定A、B、C、D的化学式。
??解：设A的化学式为ＸａＹｂ，Ｂ的化学式为Ｚｅ，则原式可改写为：2ＹａＹｂ＋3Ｚｅ＝6Ｃ＋Ｄ，按原子守恒定律：2（ａ＋ｂ）＋3ｅ＝2×6＋2＝14
??整理后得：ａ＋ｂ＋（3／2）ｅ＝7，ａ、ｂ、ｅ为正整数，ｅ＝2。
??若ｅ＝2，得ａ＝4－ｂ。
??讨论：（1）当ｂ＝1，ａ＝3?则：
??2Ｘ３Ｙ＋3Ｚ2＝6ＸＺ＋Ｙ2
??即Ａ为Ｘ３Ｙ，Ｂ为Ｚ2，Ｃ为ＸＺ，Ｄ为Ｙ2符合题意。
??（2）当ｂ＝2，ａ＝2，则2Ｘ2Ｙ2中Ｘ、Ｙ两元素都只有4个原子，不能形成C分子，不合题意，故舍去。
??（3）当ｂ＝3，ａ＝1，则：
??2ＸＹ３＋3Ｚ2＝6ＹＺ＋Ｘ2
??即A为ＸＹ３，Ｂ为Ｚ2，Ｃ为ＹＺ，Ｄ为Ｘ2符合题意。
??答：略
??例3.在
??解：设气态烯烃分子式为ＣＮＨ2Ｎ，体积分数为ｘ。
? ＣＮＨ2Ｎ＋（3／2）ＮＯ2
ＮＣＯ2＋ＮＨ2Ｏ ?ΔＶ增加
?? ｘ ?? 1．5ｎｘ ? 2ｎｘ? 0．5ｎｘ－ｘ
?? 2ＣＯ＋Ｏ2
2ＣＯ2 ? ?ΔＶ减少
?? 1-ｘ ?? ?? ??（1－ｘ）／2
??概括反应前后体积不变，即体积守恒：
??则有?0．5ｎｘ－ｘ＝（1－ｘ）／2，ｎｘ－ｘ＝1，ｘ＝1／（Ｎ－1）。
??讨论：（1）当Ｎ＝2时，ｘ＝1。乙烯Ｃ2Ｈ4占100%，ＣＯ为0。
??（2）当Ｎ＝3时，ｘ＝（1／2）。Ｃ３Ｈ６和ＣＯ各占50％。
??（3）当Ｎ＝4时，ｘ＝（1／3）。Ｃ4Ｈ８占33．3％，ＣＯ占66．7％。
??答：该烯烃可能的分子式及体积分数分别为：
??Ｃ2Ｈ4占100%，Ｃ３Ｈ６占50%，Ｃ4Ｈ８占33.3%。?
??例4.某气态烃与Ｏ2的混合气体，在一密闭容器中完全燃烧（设反应前后温度相同且高于
??解：据阿伏加德罗定律的推论：（ｐ１／ｐ2）＝（Ｎ１／Ｎ2）
??设该烃为ＣｘＨｙ，本题为等压，故Ｎ１＝Ｎ2。
?? ＣｘＨｙ＋［ｘ＋（ｙ／4）］Ｏ2 ｘＣＯ2＋（ｙ／2）Ｈ2Ｏ
?? 1ｍｏｌ ［ｘ＋（ｙ／4）］ｍｏｌ ｘｍｏｌ （ｙ／2）ｍｏｌ
??依题意 1＋ｘ＋（ｙ／4）＝ｘ＋（ｙ／2），解得：ｙ＝4。
??讨论：（1）当ｘ＝1、ｙ＝4为甲烷ＣＨ4
??（2）当ｘ＝2、ｙ＝4为乙烯Ｃ2Ｈ4
??（3）当ｘ＝3、ｙ＝4为丙炔或丙二烯Ｃ３Ｈ4
??（4）当ｘ＝4、ｙ＝4为乙烯基乙炔Ｃ4Ｈ4
??答：该气态烃可能为ＣＨ4、Ｃ2Ｈ4、Ｃ３Ｈ4、Ｃ4Ｈ4。
??此类型的题在高考和竞赛题中可经常碰到，解题过程对训练学生的思维能力、想像能力和知识的运用能力都很有帮助，因而在教学中应予以足够的重视。