1．“函数存在反函数”是“函数在R上减为函数”的（   ）

   A．充分而不必要条件                                    B．必要而不充分条件          

C．充分必要条件                                           D．既不充分也不必要条件

2．过原点和在复平面内对应点的直线的倾斜角为（   ）

   A．                         B．                     C．                     D．

3．不等式表示的平面区域为（   ）

4．过半径为2的球O表面上一点A作球O的截面，若OA与该截面所成的角是60°，则该截面的面积是（   ）

   A．                           B．                        C．                        D．

5．右图实线是函数的图象，它关于点A（a, a）对称. 如果它是一条总体密度曲线，则正数a的值为（   ）

   A．                     B．1                 C．2           D．

6．已知a、b、m、n、x、y均为正数，且，若a、m、b、x成等差数列，a、n、b、y成等比数列，则有（   ）

   A．m>n, x>y             B．m>n, x<y             C．m<n, x<y             D．m<n, x>y

7．正三棱锥V―ABC的底面边长为2a，E、F、G、H分别是VA、VB、BC、AC的中点，则四边形EFGH的面积的取值范围是（   ）

   A．              B．      C．      D．

8．已知不等式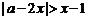，对任意恒成立，则a的取值范围为（   ）

   A．                                  B．

   C．（1，5）                                                D．（2，5）

9．如图所示，设P为△ABC所在平面内的一点，并且

则△ABP与△ABC的面积之比等于（   ）

   A．                       B．                   

  C．                  D．

10．在如图所示的10块地上选出6块种植A₁、A₂、…、A₆等六个不同品种的蔬菜，每块种植一种不同品种蔬菜，若A₁、A₂、A₃必须横向相邻种在一起，A₄、A₅横向、纵向都不能相邻种在一起，则不同的种植方案有（   ）

    A．3120                   B．3360                   C．5160                   D．5520

11．函数的定义域为，值域为，则的最小值为___________.

12．若双曲线的左焦点在抛物线的准线上，则p的值为__________.

13．某种基金今天的指数是2，以后每一天的指数都比上一天的指数增加0.2%，则100天以后这种基金的指数约是___________（精确到0.001）.

14．已知函数，若存在一个实数x，使与均不是正数，则实数m的取值范围是________________.

15．对大于或等于2的自然数m的n次幂进行如右图的方式“分裂”，仿此，5²的“分裂”中最大的数是__________，若m³的“分裂”中最小的数是211，则m的值为__________.

16．（本小题满分13分）在△ABC中，A、B、C的对边分别为a、b、c，且成等差数列.（Ⅰ）求B的值；（Ⅱ）求的范围.

16．（Ⅰ），∴，

∴，∴

（Ⅱ）

，∴，

∴

17．（本小题满分13分）在奥运会射箭决赛中，参赛号码为1~4号的四名射箭运动员参加射箭比赛。（Ⅰ）通过抽签将他们安排到1~4号靶位，试求恰有两名运动员所抽靶位号与其参赛号码相同的概率；（Ⅱ）记1号、2号射箭运动员射箭的环数为（所有取值为0，1，2，3．．．，10）分别为、.根据教练员提供的资料，其概率分布如下表：

0

1

2

3

4

5

6

7

8

9

10

0

0

0

0

0.06

0.04

0.06

0.3

0.2

0.3

0.04

0

0

0

0

0.04

0.05

0.05

0.2

0.32

0.32

0.02

①若1，2号运动员各射箭一次，求两人中至少有一人命中9环的概率；

    ②判断1号，2号射箭运动员谁射箭的水平高？并说明理由．

17．（Ⅰ）从4名运动员中任取两名，其靶位号与参赛号相同，有种方法，另2名运动员靶位号与参赛号均不相同的方法有1种，所以恰有一名运动员所抽靶位号与参赛号相同的概率为 

   （Ⅱ）①由表可知，两人各射击一次，都未击中9环的概率为P=（1-0.3）（1-0.32）=0.476至少有一人命中9环的概率为p=1-0.476=0.524

②   

所以2号射箭运动员的射箭水平高.

18．（本小题满分13分）如图，在梯形ABCD中，平面平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上.（Ⅰ）求证：平面ACFE；（Ⅱ）当EM为何值时，平面BDF？证明你的结论；（Ⅲ）求二面角B―EF―D的大小.

（Ⅰ）在梯形ABCD中，∵，

∴四边形ABCD是等腰梯形，

且

∴，∴

又∵平面平面ABCD，交线为AC，∴平面ACFE.

（Ⅱ）当时，平面BDF. 在梯形ABCD中，设，连结FN，则

∵而，∴∴MFAN，

∴四边形ANFM是平行四边形. ∴

又∵平面BDF，平面BDF. ∴平面BDF.

（Ⅲ）取EF中点G，EB中点H，连结DG、GH、DH，∵DE=DF，∴

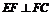∵平面ACFE，∴  又∵，∴又∵，∴∴是二面角B―EF―D的平面角.

在△BDE中∴∴，

∴又∴在△DGH中，

由余弦定理得即二面角B―EF―D的大小为

19．（本小题满分12分）如图，已知中心在原点O、焦点在x轴上的椭圆C的离心率为，点A、B分别是椭圆C的长轴、短轴的端点，点O到直线AB的距离为（Ⅰ）求椭圆C的方程；（Ⅱ）已知点E（3，0），设点P、Q是椭圆C上的两个动点，满足，求的最小值.

（Ⅰ）设椭圆方程为，则有，∴a=6, b=3.∴椭圆C的方程为

（Ⅱ），设点，则∴，∵，∴，∴∴的最小值为6.

20．（本小题满分12分）已知函数.（Ⅰ）判断函数在区间上的单调性并加以证明；（Ⅱ）求函数的值域；（Ⅲ）如果关于x的方程有三个不同的实数解，求实数k的取值范围.

20．（Ⅰ）设，，

∴在单调递增.

(Ⅱ)当时，，又，，即；

  当时，，，由，得或.

的值域为

（Ⅲ）当x=0时，，∴x=0为方程的解.

当x>0时，，∴，∴

当x<0时，，∴，∴

即看函数

与函数图象有两个交点时k的取值范围,应用导数画出的大致图象，

∴，∴

21．（本小题满分12分）设函数，，数列满足：.（Ⅰ）当时，比较x与的大小；（Ⅱ）求数列的通项公式；（Ⅲ）求证：．

21．（Ⅰ）当时， ，∴，令 有x=0，

当单调递减；当单调递增.

∴∴；

（Ⅱ）∵，∴∴

∴为首项是1、公比为的等比数列. ∴∴；

（Ⅲ）∵，由（1）知，

∴，即证．

1．B  2．D  3．A  4．A  5．A  6．B  7．B  8．B  9．C  10．C

11．     12．4       13．2.442       14．       15．9，15