1. 已知△ABC中，∠A、∠B、∠C的对边分别是a、b、c，若a、b是关于x的

    答案：直角三角形

则∠A=_____________度。

    答案：90

  3. 已知△ABC中，a、b、c分别是∠A、∠B、∠C的对边，若抛物线

    答案：直角三角形

  4. 在直角坐标系中，两圆的圆心都在y轴上，并且两圆相交于A、B两点，若点A的

    答案：

  5. 设两圆半径分别为2、5，圆心距d使点A（6－2d，7－d）在第二象限，判断两圆位置关系___________。

    答案：两圆相交

  6. a、b、c为△ABC的三条边，满足条件点（a－c，a）与点（0，－b）关于x轴对称，判断△ABC的形状____________。

    答案：等边三角形

  7. 如图所示，AD为⊙O的直径，一条直线l与⊙O交于E、F两点，过A、D分别作直线l的垂线，垂足是B、C，连结CD交⊙O于G。

    （1）求证：AD?BE=FG?DF；

    （2）设AB=m，BC=n，CD=p，求证：tan∠FAD、tan∠BAF是方程

用几何知识，视为方程根用方程知识）

    解：（1）提示：证明CF=BE，△GFC∽△ADF；

    （2）提示：先证明Rt△DFC∽Rt△FAB

    得DF：FA=FC：AB=DC：FB

    解：a＝3或a＝－1

    提示：

    将式①、②代入后，解得a＝3，a＝－1，检验适合。

  9. △ABC中，AD是高，AD与AB的夹角为锐角α，Rt△ABC的面积和周长都为

“代数式”作为方程的系数）

    解：（1）

    提示：

    （2）

    提示：

  10. 如图所示，以正方形ABCD平行于边的对称轴为坐标轴建立直角坐标系，若正方形的边长为4。

    （1）求过B、E、F三点的二次函数的解析式；

    （2）求此抛物线的顶点坐标。

    （先转化为点的坐标，再求函数解析式）

    解：（1）

    提示：点B（－2，－2），点E（0，2），点F（2，0）；

    （2）

  11. 如图所示，在△ABC中，∠B=90°，AB=6厘米，BC=3厘米，点P从点A开始沿AB边向B以1厘米/秒的速度移动，点Q从点B开始沿BC边向点C以2厘米/秒的速

米？（把实际问题转化为几何问题）

    解：

    提示：

的左侧）的横坐标的平方和为10。

    （1）求此抛物线的解析式。

    *（2）若Q是抛物线上异于A、B、P的点，且∠QAP=90°，求点Q的坐标。（利用“点坐标的绝对值等于线段长”沟通函数与几何，转化为点坐标用函数知识，转化为线段长用几何知识）

    解：（1）

    提示：∵顶点P在直线y＝－4x上，

    ∴P（1，－4）或（－1，4）。

    ∵抛物线开口向上，又与x轴有交点，

    ∴（－1，4）不合题意舍去。

    （2）

    提示：如图所示，设抛物线上点Q（m，n），过Q作QP⊥x轴于点M。

    ∵∠QAP=90°，

    由勾股定理，得

函数知识，视为方程的根用方程知识）。

    解：

    提示：

    其中C₁（2，1）不符合题意，舍去。

  1. 在下列二次根式中，最简二次根式有（    ）

    A. 1个                                B. 2个                                        C. 3个                                        D. 4个

  2. 为适应经济的发展，提高铁路运输能力，铁道部决定提高列车运行的速度，甲、乙两城市相距300千米，客车的行车速度每小时比原来增加了40千米，因此，从甲市到乙市运行的时间缩短了1小时30分，若设客车原来的速度为每小时x千米，则依题意列出的方程是（    ）

    A.                                                  B.

    C.                                                  D.

  3. 对二次函数进行配方，其结果及顶点坐标是（    ）

    A.                             B.

    C.                                 D.

  4. 下列图形中，是轴对称图形但不是中心对称图形的是（    ）

    A. 平行四边形                   B. 菱形                           C. 直角梯形                       D. 等边三角形

  5. 已知两圆的半径分别为2cm、5cm，两圆有且只有三条公切线，则它们的圆心距一定（    ）

    A. 大于3cm且小于7cm       B. 大于7cm                     C. 等于3cm                        D. 等于7cm

  1. 分解因式  ______________________。

  2. 用换元法解方程  原方程化为关于y的一元二次方程是____________。

  3. 已知△ABC中，DE交AB于D，交AC于E，且DE∥BC，=1：3，则DE：BC=____________，若AB=8，则DB=____________。

  4. 函数的自变量取值范围是____________。

  5. △ABC中，∠C=90°，，tanB=____________。

  7. 一组数据：10，8，16，34，8，14中的众数、中位数、平均数依次是______________________________________________。

  8. 圆锥的母线长为10cm，高为8cm，则它的侧面积是____________。（结果保留4个有效数字，π取3.142）

  1. 计算：

  2. 解方程组

  3. 先化简再求值：。（其中）

  1. 已知：如图所示，正方形ABCD，E为CD上一点，过B点作BF⊥BE于B，求证：∠1=∠2。

  2. 已知：如图所示，Rt△ABC中，∠C=90°，∠ABC=60°，DC=11，D点到AB的距离为2，求BD的长。

五、（第1题8分，第2题10分，共18分）

  1. 某水果批发市场规定，批发苹果不少于100千克，批发价为每千克2.5元，学校采购员带现金2000元，到该批发市场采购苹果，以批发价买进，如果采购的苹果为x（千克），付款后剩余现金为y（元）。

    （1）写出y与x间的函数关系式，并写出自变量x的取值范围，画出函数图象；

    （2）若采购员至少留出500元去采购其他物品，则它最多能购买苹果多少千克？

  2. 如图所示，⊙O中，弦AC、BD交于E，。

    （1）求证：；

    （2）延长EB到F，使EF=CF，试判断CF与⊙O的位置关系，并说明理由。

六、（本题10分）

    已知关于x的方程  ①的两实根的乘积等于1。

    （1）求证：关于x的方程    方程②有实数根；

    （2）当方程②的两根的平方和等于两根积的2倍时，它的两个根恰为△ABC的两边长，若△ABC的三边都是整数，试判断它的形状。

七、（本题10分）

    如图所示，已知BC是半圆O的直径，△ABC内接于⊙O，以A为圆心，AB为半径作弧交⊙O于F，交BC于G，交OF于H，AD⊥BC于D，AD、BF交于E，CM切⊙O于C，交BF的延长线于M，若FH=6，，求FM的长。

八、（本题12分）

    如图所示，抛物线与x轴交于A、B两点（点A在点B的左边），在第二象限内抛物线上的一点C，使△OCA∽△OBC，且AC：BC=：1，若直线AC交y轴于P。

    （1）当C恰为AP中点时，求抛物线和直线AP的解析式；

    （2）若点M在抛物线的对称轴上，⊙M与直线PA和y轴都相切，求点M的坐标。

试题答案

  1. B                           2. B                     3. C                     4. C                     5. D                     6. D

  1.

  2.

  3. 1：2，4

  4.

  5.

  6.

  7. 8，12，15

  8. 188.5cm²

  2.

  3. 原式=。

    ∵∠3+∠5=90°，（已知BF⊥BE于B），

    ∠4+∠5=90°（四边形ABCD是正方形），

    ∴∠3=∠4，

    ∵正方形ABCD，

    ∴AB=BC，∠C=∠BAF=90°。

    在Rt△ABF和Rt△CBE中，

    ∴△ABF≌△CBE（AAS），

    ∴∠1=∠2。

  2. 解：过D点作DE⊥AB于E，则DE=2，

    在Rt△ABC中，∵∠ABC=60°，

    ∴∠A=30°。

    在Rt△ADE中，∵DE=2，

    ∴AD=4，AE=，

    ∵DC=11，∴AC=11+4=15，∴AB

    ∴，

    在Rt△DEB中，，

    ∴BD=14。

五、1. 解：（1），

    （2）千克。

    答：最多购买600千克。

  2. 证明：（1）连结BC，∠ABD=∠C（∵），∠CAB公用，

    ∴△ABE∽△ABC，∴

    ∴。

    （2）连结AO、CO，设∠OAC=∠1，∠OCA=∠2，

    ∵A为中点，∴AO⊥DB，

    ∴∠1+∠AED=90°

    ∵∠AED=∠FEC，∴∠1+∠FEC=90°，

    又EF=CF，∴∠FEC=∠ECF，

    ∵AO=OC，∴∠1=∠2，

    ∴∠1+∠FEC=∠2+∠ECF=90°，

    ∴FC与⊙O相切。

六、证明：由方程①两实根乘积等于1，

    ∴经检验m=±1是方程的根。

    当m=1时，符合题意。

    m=－1时，。

    ∴。

    方程②  。

    当k=2时，方程②为，有实根。

    当时，方程②为。

      。

    ∵，

    ∴方程②有实根。

    （2）方程②  ，

    ，

    ∵

    ∴，

    ∴，

    ∴k=3，当k=3时，。

    ∵△ABC三边均为整数，

    ∴设第三边为n，则，∴。

    ∵。

    当n=2时，△ABC为等边三角形。

    当n=1或3时，△ABC为等腰三角形，n=1时，是等腰锐角三角形。

    n=3时，是等腰钝角三角形。

七、解：∵A为⊙A的圆心，∴AB=AF，∴，∵AD⊥BC，BC为⊙O直径。

    又∠ABC+∠ACB=90°，∠ABD+∠BAD=90°，

    ∴∠BAD=∠ACB，∴∠AFB=∠BAD，

    ∴∠AFB=∠ACB，∴，∴∠BAE=∠ABE，∴AE=BE。

    设∴BD=4k。

    过A作AQ⊥FH于Q，连结AO，AO垂直平分BF，易知∠ABE=∠AFB。

    ∵OB=OF，∴∠OBF=∠OFB，∴∠AFQ=∠ABD，

    ∴△ABD≌△AFQ。

    ∴AD=AQ，BG=FH=6，

    ∵AB=AG，又AD⊥BG，∴BD=DG=4k。

    BG=8k=6，∴。

    ∵∠BAC=90°，∠ADB=90°，∴AD²=BD?DC。

    ∴

    ∴BC=4k+16k=20k。

    ∵MC是⊙O切线，∴MC⊥BC，△BED∽△BMC。

    ∴。∴MC=15k。

    在Rt△BMC中，。

    由切割线定理，，

    ∴。

八、解：（1）设与x轴交于A、B两点，A（x₁，0）、B（x₂，0）。

    在Rt△APO中，∵C为AP中点，∴

    ∵△OCA∽△OBC，∴。

    设，

    ∴。

    在△ABC中，∵。

    ∵，

    ∴。

    ∴A（－6，0），B（－2，0），∴OP。

    设AP直线，A（－6，0）代入。

    。

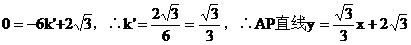    （2）设抛物线的对称轴为M₁M₂，由题意M₁到y轴距离⊥AP的垂足）。

    同理。

    ∵。

    ∴M₁和M₂的横坐标均为－4。

    设M₁M₂与AP交于Q点，，

    ∵

    ∴∠PAO=30°，∠AQM₂=60°。

    将Q点横坐标－4代入直线AP方程：

    。

    ∵，∴。

    ∴，

    ∴。

    ∴M₂点的纵坐标，

    ∴M₂（－4，）。

    综上，抛物线：，

    。

y