-
网址:http://m.1010jiajiao.com/paper/timu/5160605.html[举报]
18、(本小题满分15分)在等差数列
 中,
中,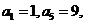 在数列
在数列 中,
中,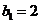 ,且
,且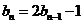 ,(n≥2)
,(n≥2)(1)求数列
 和
和 的通项公式;
的通项公式;(2)设
 求
求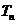 .
. - 题目来源:08高考数学模拟试卷(二) 班级 姓名 成绩
2008年江苏省镇江中学高三数学模拟试卷(二)参考答案
一、填空题(本大题共14个小题,每小题5分,共70分。)
1、已知全集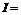 {
{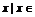 R },集合
R },集合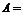 {
{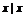 ≤1或
≤1或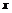 ≥3},集合
≥3},集合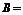 {
{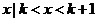 ,
, },且
},且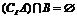 ,则实数
,则实数 的取值范围是
的取值范围是 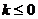 或
或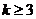
2、已知 ,则
,则 的值是
3
的值是
3
3、设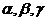 为两两不重合的平面,
为两两不重合的平面,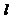
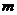
 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若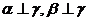 ,则
,则 ;②若
;②若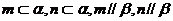 ,则
,则 ;
;
③若 ,
,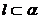 ,则
,则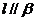 ;④若
;④若 ,则
,则 。
。
其中正确命题的个数有2个
4、点M(a,b)(ab≠0)是圆C:x2 + y2 = r2内一点,直线 是以M为中点的弦所在的直线,直线
是以M为中点的弦所在的直线,直线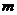 的方程是ax + by =
r2,那么直线
的方程是ax + by =
r2,那么直线 与直线
与直线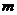 的关系是平行。
的关系是平行。
5、在等比数列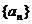 中,如果
中,如果 是一元二次方程
是一元二次方程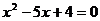 的两个根,那么
的两个根,那么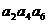 的值为
的值为

6、函数 在(-1,1)上存在
在(-1,1)上存在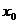 ,使
,使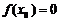 ,则a的取值范围是
,则a的取值范围是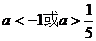
7、定义在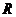 上的奇函数
上的奇函数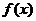 ,满足
,满足 ,
,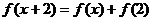 ,则
,则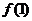 等于
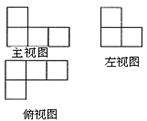
等于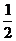 8、下图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体的个数是5个
8、下图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体的个数是5个
|
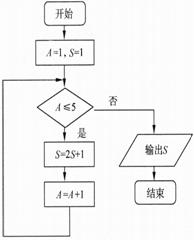
9、如图,该程序运行后输出的结果为 63 .
10、若函数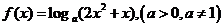 在区间
在区间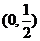 内恒有
内恒有 ,则
,则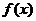 的单调递增区间是
的单调递增区间是 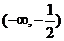
11、已知 且a≠1,
且a≠1, 当
当 ∈[-1,1]时,均有
∈[-1,1]时,均有 ,
,
则实数a的范围是
12、等差数列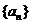 中,
中,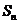 是其前n项和,
是其前n项和,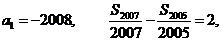
则 的值为
的值为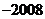 .
.
13、设椭圆 上存在两点关于直线
上存在两点关于直线 对称,则
对称,则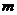 的取值范围是
的取值范围是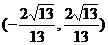
14.给出下列四个命题,其中不正确命题的序号是①②④.
①若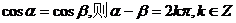 ;②函数
;②函数 的图象关于x=
的图象关于x=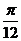 对称;
对称;
③函数 为偶函数,④函数
为偶函数,④函数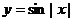 是周期函数,且周期为2
是周期函数,且周期为2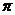 ;
;
二、解答题(本大题共6小题,共90分. 解答应写出文字说明,证明过程或演算步骤)
15、 (本小题满分15分)已知函数
⑴ 当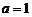 时,求
时,求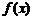 的单调递增区间;
的单调递增区间;
⑵ 当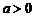 ,且
,且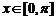 时,
时,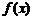 的值域是
的值域是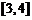 ,求
,求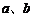 的值.
的值.
解:(1)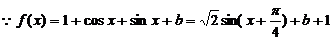
所以递增区间为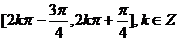
 (2)
(2)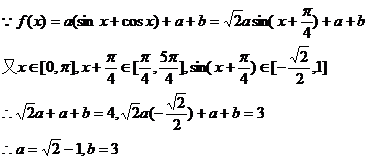
16、(本小题满分15分)
设 点为坐标原点,曲线
点为坐标原点,曲线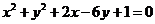 上有两点
上有两点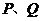 满足关于直线
满足关于直线 对称,又满足
对称,又满足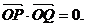
(1)求m的值;
(2)求直线PQ的方程.
解:(1)曲线方程为 ,表示圆心为(-1,3),半径为3的圆.
,表示圆心为(-1,3),半径为3的圆.
 ∴圆心(-1,3)在直线上,
∴圆心(-1,3)在直线上,
代入直线方程得 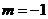 .
.
(2)∵直线PQ与直线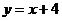 垂直,
垂直, 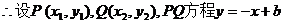
将直线 代入圆方程. 得
代入圆方程. 得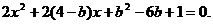

由韦达定理得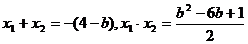

17、(本小题满分15分)
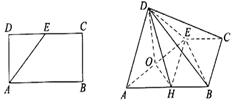
已知矩形ABCD中,AB=2AD=4,E为 CD的中点,沿AE将 AED折起,
AED折起,
|
 ,O、H分别为AE、AB的中点.
,O、H分别为AE、AB的中点.
(1)求证:直线OH//面BDE;
(2)求证:面ADE 面ABCE;
面ABCE;
解:(1)证明∵O、H分别为AE、AB的中点
∴OH//BE,又OH不在面BDE内 ∴直线OH//面BDE……………………6分
(2) O为AE的中点AD=DE,∴DQ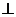 AE ∵DO=
AE ∵DO=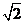 ,DB=2
,DB=2 ,
,
BO2=32+12=10∴ ∴
∴ 又因为AE和BO是相交直线
又因为AE和BO是相交直线
所以,DO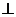 面ABCE, 又OD在面ADE内 ∴面ADE
面ABCE, 又OD在面ADE内 ∴面ADE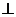 面ABCE
面ABCE
18、(本小题满分15分)
在等差数列 中,
中,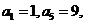 在数列
在数列 中,
中,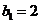 ,且
,且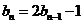 ,(n≥2)
,(n≥2)
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设 求
求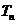 .
.
解:(1) an=2n-1
由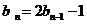 ,得:bn-1=2(bn-1-1)
(n≥2)
,得:bn-1=2(bn-1-1)
(n≥2)
∴ 是以
是以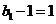 为首项,2为公比的等比数列;
为首项,2为公比的等比数列;
∴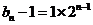 故bn=2n-1+1
故bn=2n-1+1
(2) 
 ①
①
则 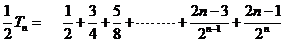 ②
②
①-②可得:
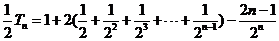
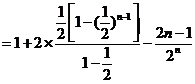
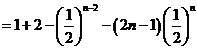
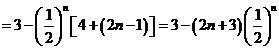
所以
19、(本小题满分15分)
某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2。(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润约为多少万元?(精确到1万元)。
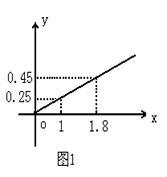

解:(I)由图象知,A,B两种产品的利润表示为投资的函数分别为:
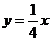 ;
;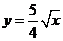
(Ⅱ)设给B投资x万元,则给A投资10-x万元,利润为y万元,

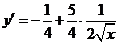
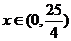 时,
时, ;
;
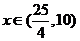 时,
时,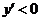 ,所以
,所以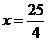 时,y有极大值.
时,y有极大值.
又函数在定义域上只有一个极值点,所以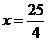 时,y有最大值
时,y有最大值
即,给A投资 万元,给B投资
万元,给B投资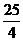 万元时,企业可获最大利润约为4万元。
万元时,企业可获最大利润约为4万元。
20、 (本小题满分14分)
已知函数:
(1)当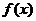 的定义域为
的定义域为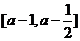 时,求函数
时,求函数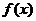 的值域;
的值域;
(2)设函数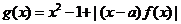 ,求函数
,求函数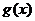 的最小值。
的最小值。
(1)解:

(2)

①若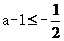 且
且 ,即
,即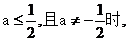
当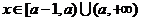 时,
时,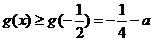
当 时,
时,
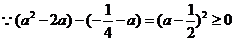
即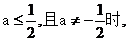 函数的最小值为
函数的最小值为 ………9分
………9分
②若 ,
,
当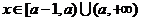 时,
时,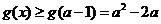
当 时,
时, 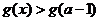
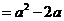
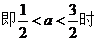 ,函数的最小值为
,函数的最小值为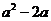 ………11分
………11分
③若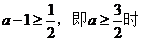 ,
,
当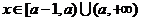 时,
时,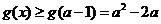
当 时,
时,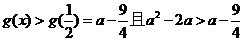
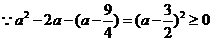
即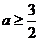 时,函数的最小值为
时,函数的最小值为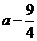 ………13分
………13分
综上可得:
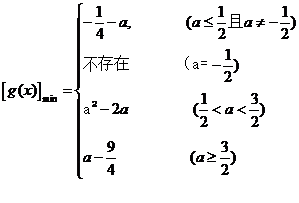 ………15分
………15分