-
网址:http://m.1010jiajiao.com/paper/timu/5160358.html[举报]
5.()已知函数f(x)=ax+
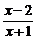 (a>1).
(a>1).(1)证明:函数f(x)在(-1,+∞)上为增函数.
(2)用反证法证明方程f(x)=0没有负数根.
- 题目来源:08高考数学奇偶性与单调性测试 函数的单调性、奇偶性是高考的重点内容之一,考查内容灵活多样.本节主要帮助考生深刻理解奇偶性、单调性的定义,掌握判定方法,正确认识单调函数与奇偶函数的图象. ●难点磁场 ()设a>0,f(x)=是R上的偶函数,(1)求a的值;(2)证明: f(x)在(0,+∞)上是增函数. ●案例探究 [例1]已知函数f(x)在(-1,1)上有定义,f()=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(),试
参考答案
难点磁场
(1)解:依题意,对一切x∈R,有f(x)=f(-x),即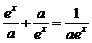 +aex.整理,得(a-
+aex.整理,得(a-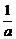 )
)
(ex-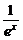 )=0.因此,有a-
)=0.因此,有a-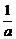 =0,即a2=1,又a>0,∴a=1
=0,即a2=1,又a>0,∴a=1
(2)证法一:设0<x1<x2,则f(x1)-f(x2)=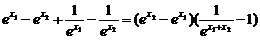
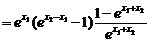
由x1>0,x2>0,x2>x1,∴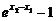 >0,1-e
>0,1-e <0,
<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2)
∴f(x)在(0,+∞)上是增函数
证法二:由f(x)=ex+e-x,得f′(x)=ex-e-x=e-x.(e2x-1).当x∈(0,+∞)时,e-x>0,e2x-1>0.
此时f′(x)>0,所以f(x)在[0,+∞)上是增函数.
歼灭难点训练
一、1.解析:f(-x)=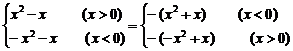 =-f(x),故f(x)为奇函数.
=-f(x),故f(x)为奇函数.
答案:C
2.解析:f(-x)=-f(x),f(x)是奇函数,图象关于原点对称.
答案:C
二、3.解析:令t=|x+1|,则t在(-∞,-1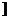 上递减,又y=f(x)在R上单调递增,∴y=f(|x+1|)在(-∞,-1
上递减,又y=f(x)在R上单调递增,∴y=f(|x+1|)在(-∞,-1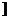 上递减.
上递减.
答案:(-∞,-1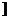
4.解析:∵f(0)=f(x1)=f(x2)=0,∴f(0)=d=0.f(x)=ax(x-x1)(x-x2)=ax3-a(x1+x2)x2+ax1x2x,
∴b=-a(x1+x2),又f(x)在[x2,+∞ 单调递增,故a>0.又知0<x1<x,得x1+x2>0,
单调递增,故a>0.又知0<x1<x,得x1+x2>0,
∴b=-a(x1+x2)<0.
答案:(-∞,0)
三、5.证明:(1)设-1<x1<x2<+∞,则x2-x1>0,  >1且
>1且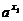 >0,
>0,
∴ >0,又x1+1>0,x2+1>0
>0,又x1+1>0,x2+1>0
∴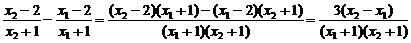 >0,
>0,
于是f(x2)-f(x1)=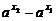 +
+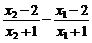 >0
>0
∴f(x)在(-1,+∞)上为递增函数.
(2)证法一:设存在x0<0(x0≠-1)满足f(x0)=0,则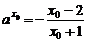 且由0<
且由0<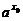 <1得0<-
<1得0<-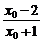 <1,即
<1,即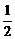 <x0<2与x0<0矛盾,故f(x)=0没有负数根.
<x0<2与x0<0矛盾,故f(x)=0没有负数根.
证法二:设存在x0<0(x0≠-1)使f(x0)=0,若-1<x0<0,则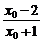 <-2,
<-2,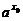 <1,∴f(x0)<-1与f(x0)=0矛盾,若x0<-1,则
<1,∴f(x0)<-1与f(x0)=0矛盾,若x0<-1,则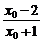 >0,
>0, 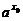 >0,∴f(x0)>0与f(x0)=0矛盾,故方程f(x)=0没有负数根.
>0,∴f(x0)>0与f(x0)=0矛盾,故方程f(x)=0没有负数根.
6.证明:∵x≠0,∴f(x)=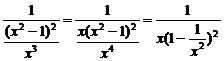 ,
,
设1<x1<x2<+∞,则 .
.
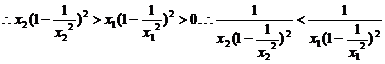
∴f(x1)>f(x2),故函数f(x)在(1,+∞)上是减函数.(本题也可用求导方法解决)
7.证明:(1)不妨令x=x1-x2,则f(-x)=f(x2-x1)=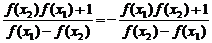
=-f(x1-x2)=-f(x).∴f(x)是奇函数.
(2)要证f(x+4a)=f(x),可先计算f(x+a),f(x+2a).
∵f(x+a)=f[x-(-a)]=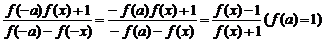 .
.
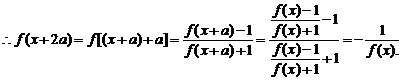
∴f(x+4a)=f[(x+2a)+2a]=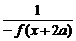 =f(x),故f(x)是以4a为周期的周期函数.
=f(x),故f(x)是以4a为周期的周期函数.
8.(1)证明:设x1<x2,则x2-x1-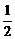 >-
>-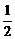 ,由题意f(x2-x1-
,由题意f(x2-x1-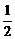 )>0,
)>0,
∵f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)+f(x1)-1-f(x1)=f(x2-x1)-1=f(x2-x1)+f(-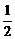 )-1=f[(x2-x1)-
)-1=f[(x2-x1)-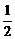 ]>0,
]>0,
∴f(x)是单调递增函数.
(2)解:f(x)=2x+1.验证过程略.