-
网址:http://m.1010jiajiao.com/paper/timu/5160318.html[举报]
16.在平面直角坐标系
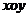 中,已知
中,已知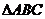 顶点
顶点 和
和 ,顶点
,顶点 在椭圆
在椭圆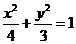 上,则
上,则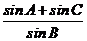 的值是 (
)
的值是 (
)A.0 B.1 C.2 D.不确定
- 题目来源:高考数学学科复习测试试题 数学试题 第Ⅰ卷(48分) 1.试卷中使用向量的符号表示意义相同. 2.本试卷共有22道题,满分150分,考试时间120分钟. 3.本试卷为文、理合卷,题首标有文科考生做、理科考生做的题目,没有标记的是“文”、 “理”考生共同做的题目.
参考答案
说明
1.本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中
|
2.评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的
评阅. 当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变
这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过
后面部分应给分数之半,如果有较严重的概念性错误,就不给分.
3.第17题至第22题中右端所注的分数,表示考生正确做到这一步应得的该题累加分
数.
4.给分或扣分均以1分为单位.
一、(第1至12题)每一题正确的给4分,否则一律得零分.
1.arctan3;
2..  ; 3. 若
; 3. 若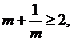 则m>0; 4.
则m>0; 4. 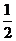
5. p; 6. 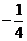 ;
7. (文) 1(理)
;
7. (文) 1(理) ; 8.
; 8. 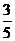 ;
;
9.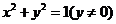 ;
10.
;
10. 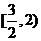 11. y=1
12. ③.
11. y=1
12. ③.
二、(第13至16题)每一题正确的给4分,否则一律得零分.
13.B 14.A 15.B 16.C
三、(第17至22题)
17.(文)[解一]设z=a+bi(a、bÎR ,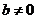 )
……………………2分
)
……………………2分
由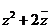 =
=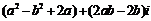
∵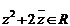 ,
∴
,
∴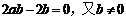 ,
,
∴a=1, ……………………8分
又|z|= , 即
, 即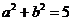 ,∴b=
,∴b=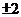 , ∴z=1
, ∴z=1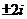 . …………………12分
. …………………12分
[解二] 设z=a+bi(a、bÎR ,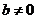 )
)
则
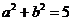 ∵
∵ ,
,
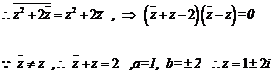
(参考解法一评分标准给分)
(理) [解一]设z=x+yi(x、yÎR ,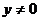 )
……………………2分
)
……………………2分
由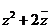 =
=
∵ ,
∴
,
∴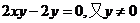 ,
,
∴x=1, ……………………-8分
又|z|= , 即
, 即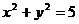 , ∴y=
, ∴y=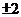 , ∴z=1
, ∴z=1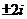 .
.
∵ z虚部为正数, ∴y=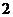 , ∴z=1
, ∴z=1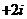 ,
,
∴w=1+2i+ai …………………………10分
∴|w|=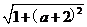 ,
aÎ[0,1]
,
aÎ[0,1]
∴|w|Î[ ,
,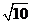 ].
……………………12分
].
……………………12分
[解二] (同文科,参考上评分标准给分)
18.[解](1)∵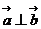 , ∴
, ∴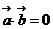 ,
…………………2分
,
…………………2分
∴sinxcosx -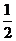 =0, sin2x=1, ……………………4分
=0, sin2x=1, ……………………4分
∴2x=2kp+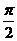 ,
∴x=kp+
,
∴x=kp+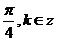 .……………………-6分
.……………………-6分
(2)(文)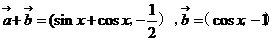
f(x)=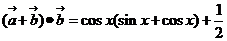 ……………………8分
……………………8分
=sinxcosx+cos2x+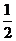
=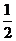 sin2x+
sin2x+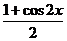 +
+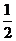
=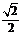 sin(2x+
sin(2x+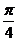 )+1
……………………10分
)+1
……………………10分
∴f(x)max=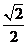 +1,f(x)max=1-
+1,f(x)max=1-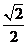 . ……………………12分
. ……………………12分
(理)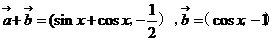
f(x)=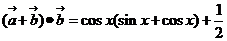 ……………………8分
……………………8分
=sinxcosx+cos2x+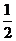
=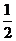 sin2x+
sin2x+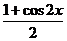 +
+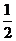
=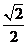 sin(2x+
sin(2x+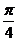 )+1
…………………9分
)+1
…………………9分
- £2x+
£2x+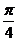 £
£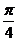 ,
……………………10分
,
……………………10分
∴f(x)max= ,
f(x)max=1-
,
f(x)max=1-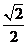 . ……………………12分
. ……………………12分
19. [解] (1)(文)
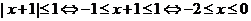
∴B[-2,0] ……………………6分
(理)A={x|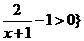
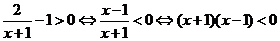 ∴ -1<x<1
∴ -1<x<1
∴A=(-1,1),定义域关于原点对称 ……………………3分
f(x)= lg ,
,
则 f(-x)=lg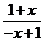 = lg
= lg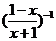 =
=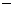 lg
lg ,
,
∴f(x)是奇函数. ……………………6分
(2)B={x|
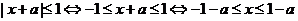
B=[-1-a,1-a] ……………………8分
当a ³2时, -1-a£-3, 1-a£-1,
由A=(-1,1),
B=[-1-a,1-a], 有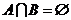 ……………11分
……………11分
反之,若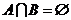 ,可取-a-1=2,则a=-3,a小于2. (注:反例不唯一)
,可取-a-1=2,则a=-3,a小于2. (注:反例不唯一)
……………………13分
所以,a ³2是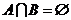 的充分非必要条件.
…………………14分
的充分非必要条件.
…………………14分
20.[解](1)每套“福娃”所需成本费用为
 …………………………3分
…………………………3分
…………………………4分
当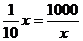 , 即x=100时,每套“福娃”所需成本费用最少为25元. ………6分
, 即x=100时,每套“福娃”所需成本费用最少为25元. ………6分
(2)利润为
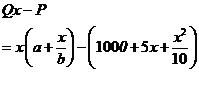 ………………………………8分
………………………………8分
=(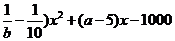 …………………---9分
…………………---9分
由题意, ……………………12分
……………………12分
解得 a= 25, b= 30. ……………………14分
21.[解](1)在等差数列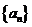 中,公差
中,公差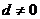 ,且
,且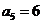 ,
,
则 ……………………3分
……………………3分
(2)在等差数列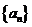 中,公差
中,公差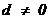 ,且
,且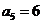 ,
,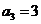
则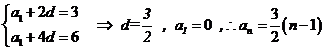
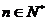 …………5分
…………5分
又 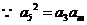 则
36=3am,
则
36=3am,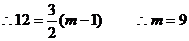 …………8分
…………8分
(文科)(3)在等差数列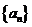 中,公差
中,公差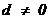 ,且
,且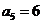 ,
,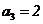
则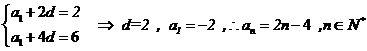 ……10分
……10分
又因为公比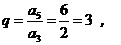 首项
首项 ,
,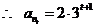 …………14分
…………14分
又因为 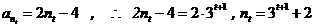
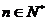
……………………16分
(理科)(3)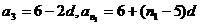
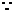
 成等比数列,
成等比数列,
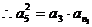

∴ …………14分
…………14分
又∵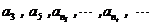 成等比数列, ∴
成等比数列, ∴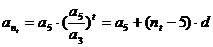
∴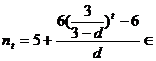 {6,7,8,9,10,…}对一切
{6,7,8,9,10,…}对一切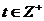 成立,
成立,
∴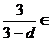 {2,3,4,5,…}(*),设
{2,3,4,5,…}(*),设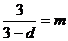 (
(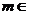 {2,3,4,5,…}),
{2,3,4,5,…}),
∴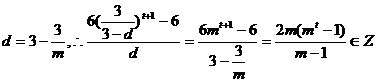 ,(由二项式定理知,
,(由二项式定理知,
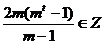 恒成立) ∴
恒成立) ∴ (
(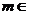 {2,3,4,5,…})
{2,3,4,5,…})
(注的证明可用无穷递降法完成,证略. ) ………………16分
22.[解](1)设过抛物线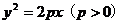 的焦点
的焦点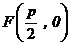 的直线方程为
的直线方程为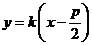
或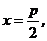 (斜率
(斜率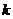 不存在)
……………………1分
不存在)
……………………1分
则
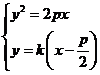 得
得 
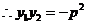 …………2分
…………2分
当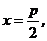 (斜率
(斜率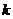 不存在)时,则
不存在)时,则
又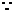
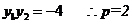 ……………………4分
……………………4分
 所求抛物线方程为
所求抛物线方程为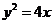
(2)[解]
设 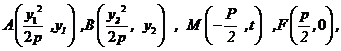
由已知直线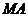 、
、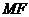 、
、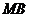 的斜率分别记为:
的斜率分别记为: 、
、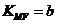 、
、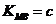 ,得
,得
 且
且
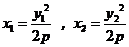 …………6分
…………6分
故
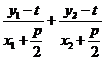



当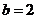 时
时 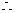
 4
………………10分
4
………………10分
(文科) [解](3)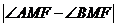 和
和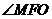 的值相等 …………12分
的值相等 …………12分
如果取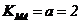 ,
,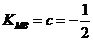 时, 则由(2)问得
时, 则由(2)问得 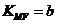
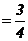
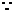

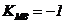 即
即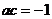 , 又由(2)问得
, 又由(2)问得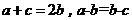
设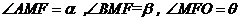
1)若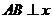 轴,则
轴,则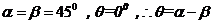 ……………………13分
……………………13分
2)若 >0
则
>0
则 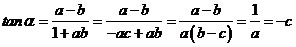
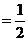
同理可得

而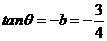
则  ,易知
,易知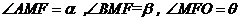 都是锐角
都是锐角
 …………………………16分
…………………………16分
3)若 <0,类似的也可证明
<0,类似的也可证明 .
.
综上所述 即
即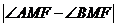 和
和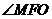 的值相等 …………18分
的值相等 …………18分
(理科) [解](3)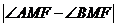 和
和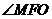 的值相等 …………10分
的值相等 …………10分
如果取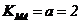 ,
,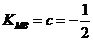 时, 则由(2)问得
时, 则由(2)问得 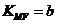
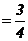
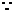

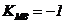 即
即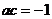 , 又由(2)问得
, 又由(2)问得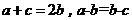
设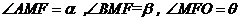
1)若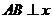 轴,则
轴,则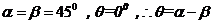 ………………11分
………………11分
2)若 >0
则
>0
则 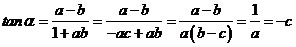
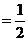
同理可得

而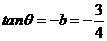
即 ,易知
,易知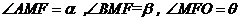 都是锐角
都是锐角
 …………………………12分
…………………………12分
3)若 <0,类似的也可证明
<0,类似的也可证明 .
.
综上所述 即
即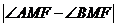 和
和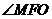 的值相等 …………13分
的值相等 …………13分
[解一](3)概括出的条件:
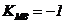 (即
(即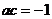 )或
)或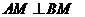 ,等
,等
…………………………14分
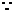

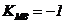 即
即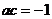 , 又由(2)问得
, 又由(2)问得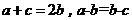
设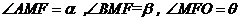
1)若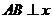 轴,则
轴,则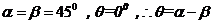 ………………15分
………………15分
2)若 >0
则
>0
则 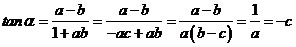
同理可得
而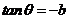 ,则
,则 ;易知
;易知
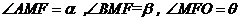 都是锐角
都是锐角
 …………………………17分
…………………………17分
3)若 <0,类似的也可证明
<0,类似的也可证明 .
.
综上所述 即
即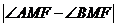 和
和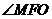 的值相等 ……18分
的值相等 ……18分
[解二] (略)(其它证法可参考上述评分标准给分)