-
网址:http://m.1010jiajiao.com/paper/timu/5160260.html[举报]
2.()函数f(x)的定义域为R,且x≠1,已知f(x+1)为奇函数,当x<1时,f(x)=2x2–x+1,那么当x>1时,f(x)的递减区间是( )
A.[
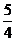 ,+∞
,+∞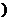 B.(1,
B.(1,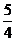
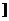 C.[
C.[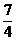 ,+∞
,+∞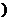 D.(1,
D.(1,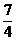 ]
] - 题目来源:难点36 函数方程思想 函数与方程思想是最重要的一种数学思想,高考中所占比重较大,综合知识多、题型多、应用技巧多.函数思想简单,即将所研究的问题借助建立函数关系式亦或构造中间函数,结合初等函数的图象与性质,加以分析、转化、解决有关求值、解(证)不等式、解方程以及讨论参数的取值范围等问题;方程思想即将问题中的数量关系运用数学语言转化为方程模型加以解决. ●难点磁场 1.()关于x的不等式2.32x–3x+a2–a–3>0,当0≤x≤1时恒成立,则实数a的取值范围为 . 2.()对于函数
参 考 答 案
●难点磁场
1.解析:设t=3x,则t∈[1,3],原不等式可化为a2–a–3>–2t2+t,t∈[1,3].
等价于a2–a–3大于f(t)=–2t2+t在[1,3]上的最大值.
答案:(–∞,–1)∪(2,+∞)
2.解:(1)当a=1,b=–2时,f(x)=x2–x–3,由题意可知x=x2–x–3,得x1=–1,x2=3.
故当a=1,b=–2时,f(x)的两个不动点为–1,3.
(2)∵f(x)=ax2+(b+1)x+(b–1)(a≠0)恒有两个不动点,
∴x=ax2+(b+1)x+(b–1),即ax2+bx+(b–1)=0恒有两相异实根
∴Δ=b2–4ab+4a>0(b∈R)恒成立.
于是Δ′=(4a)2–16a<0解得0<a<1
故当b∈R,f(x)恒有两个相异的不动点时,0<a<1.
(3)由题意A、B两点应在直线y=x上,设A(x1,x1),B(x2,x2)
又∵A、B关于y=kx+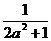 对称.
对称.
∴k=–1.设AB的中点为M(x′,y′)
∵x1,x2是方程ax2+bx+(b–1)=0的两个根.
∴x′=y′=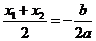 ,又点M在直线
,又点M在直线 上有
上有
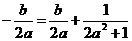 ,即
,即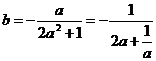
∵a>0,∴2a+ ≥2
≥2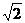 当且仅当2a=
当且仅当2a= 即a=
即a=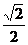 ∈(0,1)时取等号,
∈(0,1)时取等号,
故b≥– ,得b的最小值–
,得b的最小值–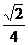 .
.
●歼灭难点训练
一、1.解析:考查函数y1= 和y2=(2a)x的图象,显然有0<2a<1.由题意
和y2=(2a)x的图象,显然有0<2a<1.由题意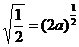 得a=
得a= ,再结合指数函数图象性质可得答案.
,再结合指数函数图象性质可得答案.
答案:A
2.解析:由题意可得f(–x+1)=–f(x+1).令t=–x+1,则x=1–t,故f(t)=–f(2–t),即f(x)=–f(2–x).
当x>1,2–x<1,于是有f(x)=–f(2–x)=–2(x–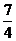 )2–
)2– ,其递减区间为[
,其递减区间为[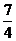 ,+∞).
,+∞).
答案:C
3.解析:显然有x>3,原方程可化为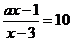
故有(10–a).x=29,必有10–a>0得a<10
又x=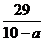 >3可得a>
>3可得a>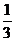 .
.
答案: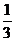 <a<10
<a<10
4.解析:原式化为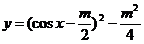 .
.
当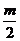 <–1,ymin=1+m=–4
<–1,ymin=1+m=–4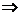 m=–5.
m=–5.
当–1≤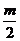 ≤1,ymin=
≤1,ymin= =–4
=–4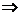 m=±4不符.
m=±4不符.
当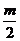 >1,ymin=1–m=–4
>1,ymin=1–m=–4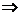 m=5.
m=5.
答案:±5
二、5.解:(1)令2x=t(t>0),设f(t)=t2–4t+a.
由f(t)=0在(0,+∞)有且仅有一根或两相等实根,则有
①f(t)=0有两等根时,Δ=0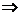 16–4a=0
16–4a=0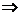 a=4
a=4
验证:t2–4t+4=0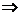 t=2∈(0,+∞),这时x=1
t=2∈(0,+∞),这时x=1
②f(t)=0有一正根和一负根时,f(0)<0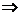 a<0
a<0
③若f(0)=0,则a=0,此时4x–4.2x=0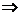 2x=0(舍去),或2x=4,∴x=2,即A中只有一个元素
2x=0(舍去),或2x=4,∴x=2,即A中只有一个元素
综上所述,a≤0或a=4,即B={a|a≤0或a=4}
(2)要使原不等式对任意a∈(–∞,0]∪{4}恒成立.即g(a)=(x–2)a–(x2–6x)>0恒成立.只须
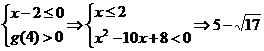 <x≤2
<x≤2
6.解:(1)∵方程ax2+bx=2x有等根,∴Δ=(b–2)2=0,得b=2.
由f(x–1)=f(3–x)知此函数图象的对称轴方程为x=–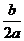 =1得a=–1,故f(x)=–x2+2x.
=1得a=–1,故f(x)=–x2+2x.
(2)f(x)=–(x–1)2+1≤1,∴4n≤1,即n≤
而抛物线y=–x2+2x的对称轴为x=1
∴n≤ 时,f(x)在[m,n]上为增函数.
时,f(x)在[m,n]上为增函数.
若满足题设条件的m,n存在,则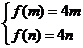
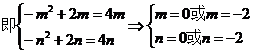
又m<n≤ ,∴m=–2,n=0,这时定义域为[–2,0],值域为[–8,0].
,∴m=–2,n=0,这时定义域为[–2,0],值域为[–8,0].
由以上知满足条件的m、n存在,m=–2,n=0.
7.(1)证明:当n=1时,g1(x0)=x0显然成立;
设n=k时,有gk(x0)=x0(k∈N)成立,
则gk+1(x0)=f[gk(x0)]=f(x0)=g1(x0)=x0
即n=k+1时,命题成立.
∴对一切n∈N,若g1(x0)=x0,则gn(x0)=x0.
(2)解:由(1)知,稳定不动点x0只需满足f(x0)=x0
由f(x0)=x0,得6x0–6x02=x0,∴x0=0或x0=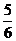
∴稳定不动点为0和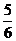 .
.
(3)解:∵f(x)<0,得6x–6x2<0 x<0或x>1.
x<0或x>1.
∴gn(x)<0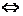 f[gn–1(x)]<0
f[gn–1(x)]<0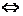 gn–1(x)<0或gn–1(x)>1
gn–1(x)<0或gn–1(x)>1
要使一切n∈N,n≥2,都有gn(x)<0,必须有g1(x)<0或g1(x)>1.
由g1(x)<0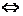 6x–6x2<0
6x–6x2<0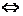 x<0或x>1
x<0或x>1
由g1(x)>0 6x–6x2>1
6x–6x2>1
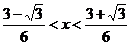
故对于区间(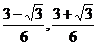 )和(1,+∞)内的任意实数x,只要n≥2,n∈N,都有gn(x)<0.
)和(1,+∞)内的任意实数x,只要n≥2,n∈N,都有gn(x)<0.
8.(1)证明:任取x1>x2>0,f(x1)–f(x2)=
∵x1>x2>0,∴x1x2>0,x1–x2>0,
∴f(x1)–f(x2)>0,即f(x1)>f(x2),故f(x)在(0,+∞)上是增函数.
(2)解:∵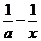 ≤2x在(0,+∞)上恒成立,且a>0,
≤2x在(0,+∞)上恒成立,且a>0,
∴a≥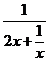 在(0,+∞)上恒成立,令
在(0,+∞)上恒成立,令 (当且仅当2x=
(当且仅当2x= 即x=
即x=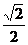 时取等号),要使a≥
时取等号),要使a≥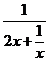 在(0,+∞)上恒成立,则a≥
在(0,+∞)上恒成立,则a≥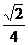 .故a的取值范
.故a的取值范
围是[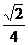 ,+∞).
,+∞).
(3)解:由(1)f(x)在定义域上是增函数.
∴m=f(m),n=f(n),即m2– m+1=0,n2–
m+1=0,n2– n+1=0
n+1=0
故方程x2– x+1=0有两个不相等的正根m,n,注意到m.n=1,故只需要Δ=(
x+1=0有两个不相等的正根m,n,注意到m.n=1,故只需要Δ=( )2–4>0,由于a>0,则0<a<
)2–4>0,由于a>0,则0<a<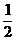 .
.