-
网址:http://m.1010jiajiao.com/paper/timu/5160230.html[举报]
6.()已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于常数λ(λ>0).求动点M的轨迹方程,并说明它表示什么曲线.
- 题目来源:难点38 分类讨论思想 分类讨论思想就是根据所研究对象的性质差异,分各种不同的情况予以分析解决.分类讨论题覆盖知识点较多,利于考查学生的知识面、分类思想和技巧;同时方式多样,具有较高的逻辑性及很强的综合性,树立分类讨论思想,应注重理解和掌握分类的原则、方法与技巧、做到“确定对象的全体,明确分类的标准,分层别类不重复、不遗漏的分析讨论.” ●难点磁场 1.()若函数在其定义域内有极值点,则a的取值为 . 2.()设函数f(x)=x2+|x–a|+1,x∈R. (1)判断函数
参 考 答 案
●难点磁场
1.解析:即f(x)=(a–1)x2+ax–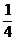 =0有解.
=0有解.
当a–1=0时,满足.当a–1≠0时,只需Δ=a2–(a–1)>0.
答案: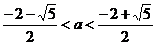 或a=1
或a=1
2.解:(1)当a=0时,函数f(–x)=(–x)2+|–x|+1=f(x),此时f(x)为偶函数.
当a≠0时,f(a)=a2+1,f(–a)=a2+2|a|+1.f(–a)≠f(a),f(–a)≠–f(a)
此时函数f(x)既不是奇函数,也不是偶函数.
(2)①当x≤a时,函数f(x)=x2–x+a+1=(x–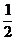 )2+a+
)2+a+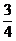
若a≤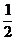 ,则函数f(x)在(–∞,a]上单调递减.
,则函数f(x)在(–∞,a]上单调递减.
从而函数f(x)在(–∞,a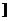 上的最小值为f(a)=a2+1
上的最小值为f(a)=a2+1
若a>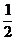 ,则函数f(x)在(–∞,a
,则函数f(x)在(–∞,a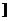 上的最小值为f(
上的最小值为f(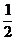 )=
)=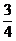 +a,且f(
+a,且f(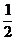 )≤f(a).
)≤f(a).
②当x≥a时,函数f(x)=x2+x–a+1=(x+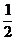 )2–a+
)2–a+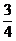
若a≤–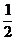 ,则函数f(x)在[a,+∞]上的最小值为f(–
,则函数f(x)在[a,+∞]上的最小值为f(–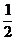 )=
)=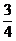 –a,且f(–
–a,且f(–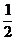 )≤f(a);
)≤f(a);
若a>–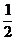 ,则函数f(x)在[a,+∞)单调递增.
,则函数f(x)在[a,+∞)单调递增.
从而函数f(x)在[a,+∞]上的最小值为f(a)=a2+1.
综上,当a≤–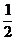 时,函数f(x)的最小值为
时,函数f(x)的最小值为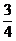 –a;
–a;
当–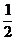 <a≤
<a≤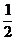 时,函数f(x)的最小值是a2+1;
时,函数f(x)的最小值是a2+1;
当a>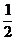 时,函数f(x)的最小值是a+
时,函数f(x)的最小值是a+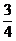 .
.
●歼灭难点训练
一、1.解析:分a=2、|a|>2和|a|<2三种情况分别验证.
答案:C
2.解析:任取4个点共C =210种取法.四点共面的有三类:(1)每个面上有6个点,则有4×C
=210种取法.四点共面的有三类:(1)每个面上有6个点,则有4×C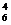 =60种取共面的取法;(2)相比较的4个中点共3种;(3)一条棱上的3点与对棱的中点共6种.
=60种取共面的取法;(2)相比较的4个中点共3种;(3)一条棱上的3点与对棱的中点共6种.
答案:C
二、3.解析:分线段AB两端点在平面同侧和异侧两种情况解决.
答案:1或2
4.解析:A={1,2},B={x|(x–1)(x–1+a)=0},
由A∪B=A可得1–a=1或1–a=2;
由A∩C=C,可知C={1}或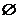 .
.
答案:2或3
3或(–2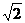 ,2
,2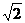 )
)
三、5.解:设x0∈A,x0是x02+px0+q=0的根.
若x0=0,则A={–2,0},从而p=2,q=0,B={–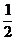 }.
}.
此时A∩B=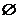 与已知矛盾,故x0≠0.
与已知矛盾,故x0≠0.
将方程x02+px0+q=0两边除以x02,得
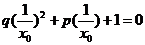 .
.
即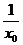 满足B中的方程,故
满足B中的方程,故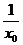 ∈B.
∈B.
∵A∩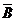 ={–2},则–2∈A,且–2∈
={–2},则–2∈A,且–2∈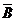 .
.
设A={–2,x0},则B={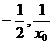 },且x0≠2(否则A∩B=
},且x0≠2(否则A∩B=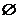 ).
).
若x0=–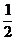 ,则
,则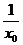 –2∈B,与–2
–2∈B,与–2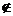 B矛盾.
B矛盾.
又由A∩B≠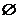 ,∴x0=
,∴x0=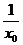 ,即x0=±1.
,即x0=±1.
即A={–2,1}或A={–2,–1}.
故方程x2+px+q=0有两个不相等的实数根–2,1或–2,–1
∴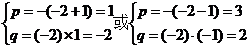
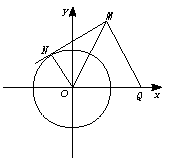 6.解:如图,设MN切圆C于N,则动点M组成的集合是P={M||MN|=λ|MQ|,λ>0}.
6.解:如图,设MN切圆C于N,则动点M组成的集合是P={M||MN|=λ|MQ|,λ>0}.
∵ON⊥MN,|ON|=1,
∴|MN|2=|MO|2–|ON|2=|MO|2–1
设动点M的坐标为(x,y),
则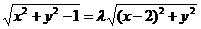
即(x2–1)(x2+y2)–4λ2x+(4λ2+1)=0.
经检验,坐标适合这个方程的点都属于集合P,故方程为所求的轨迹方程.
(1)当λ=1时,方程为x=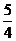 ,它是垂直于x轴且与x轴相交于点(
,它是垂直于x轴且与x轴相交于点(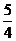 ,0)的直线;
,0)的直线;
(2)当λ≠1时,方程化为: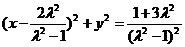
它是以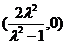 为圆心,
为圆心,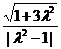 为半径的圆.
为半径的圆.
7.解:(1)依题意f(0)=0,又由f(x1)=1,当0≤y≤1,函数y=f(x)的图象是斜率为b0=1的线段,故由
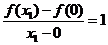
∴x1=1
又由f(x2)=2,当1≤y≤2时,函数y=f(x)的图象是斜率为b的线段,故由
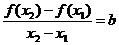
即x2–x1=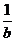
∴x2=1+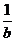
记x0=0,由函数y=f(x)图象中第n段线段的斜率为bn–1,故得
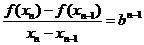
又由f(xn)=n,f(xn–1)=n–1
∴xn–xn–1=(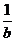 )n–1,n=1,2,……
)n–1,n=1,2,……
由此知数列{xn–xn–1}为等比数列,其首项为1,公比为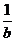 .
.
因b≠1,得 (xk–xk–1)
(xk–xk–1)
=1+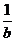 +…+
+…+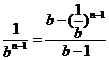
即xn=
(2)由(1)知,当b>1时,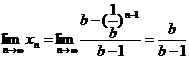
当0<b<1,n→∞, xn也趋于无穷大.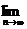 xn不存在.
xn不存在.
(3)由(1)知,当0≤y≤1时,y=x,即当0≤x≤1时,f(x)=x;
当n≤y≤n+1,即xn≤x≤xn+1由(1)可知
f(x)=n+bn(x–xn)(n=1,2,…),由(2)知
当b>1时,y=f(x)的定义域为[0,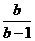 );
);
当0<b<1时,y=f(x)的定义域为[0,+∞).
8.(1)证明:依设,对任意x∈R,都有f(x)≤1
∵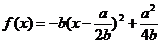
∴ ≤1
≤1
∵a>0,b>0
∴a≤2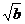 .
.
(2)证明:必要性:
对任意x∈[0,1],|f(x)|≤1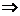 –1≤f(x),据此可以推出–1≤f(1)
–1≤f(x),据此可以推出–1≤f(1)
即a–b≥–1,∴a≥b–1
对任意x∈[0,1],|f(x)|≤1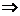 f(x)≤1.
f(x)≤1.
因为b>1,可以推出f( )≤1即a.
)≤1即a. –1≤1,
–1≤1,
∴a≤2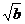 ,∴b–1≤a≤2
,∴b–1≤a≤2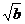
充分性:
因为b>1,a≥b–1,对任意x∈[0,1].
可以推出ax–bx2≥b(x–x2)–x≥–x≥–1
即ax–bx2≥–1
因为b>1,a≤2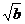 ,对任意x∈[0,1],可以推出ax–bx2≤2
,对任意x∈[0,1],可以推出ax–bx2≤2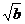 x–bx2≤1
x–bx2≤1
即ax–bx2≤1,∴–1≤f(x)≤1
综上,当b>1时,对任意x∈[0,1],|f(x)|≤1的充要条件是b–1≤a≤2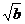 .
.
(3)解:∵a>0,0<b≤1
∴x∈[0,1],f(x)=ax–bx2≥–b≥–1
即f(x)≥–1
f(x)≤1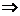 f(1)≤1
f(1)≤1 a–b≤1
a–b≤1
即a≤b+1
a≤b+1 f(x)≤(b+1)x–bx2≤1
f(x)≤(b+1)x–bx2≤1
即f(x)≤1
所以当a>0,0<b≤1时,对任意x∈[0,1],|f(x)|≤1的充要条件是a≤b+1.