参考答案

11．48　　　　　　　　　　 12．80　　　　　　　　　　 13．　　　　　　　　 14．(1，-2)　　　　　　　　　　　　 15．

16．(1)设A为“甲能译出”，B为“乙能译出”，则A、B互相独立，从而A与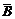、与B、与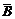均相互独立.

“恰有一人能译出”为事件，又与互斥，

则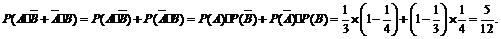

(2)“至多一人能译出”的事件，且、、互斥，

∴

(3)设至少需要n个甲这样的人，而n个甲这样的人译不出的概率为，

∴n个甲这样的人能译出的概率为，

由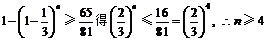

∴至少需4个甲这样的人才能满足题意.

17．(1)由得，所以，所以，因为A为的内角，所以

(2)因为，由正弦定理得

由(1)得所以∴

18．(1)∵，∴，又∵　∴

∴数列是等差数列，且

(2)当时，

当n=1时，不成立. ∴

(3)，∴.

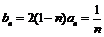∴左边显然成立.

19．(1)∵O、D分别为AC、PC的中点，∴OD∥PA. 又PA平面PAB，∴OD∥平面PAB.

(2)∵　又∵平面ABC，∴PA=PB=PC，

取BC中点E，连结PE和OE，则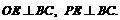

∴是所求二面角的平面角.

又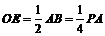，易求得　在直角中，，

∴二面角A-BC-P的大小为

20．(1)由题意有，且又曲线在原点处的切线的斜率　而直线到此切线所成的角为45°，

∴，解得b= -3.

代入得a=0，故f(x)的解析式为

(2)由可知，f(x)在和上递增；在[-1，1]上递减，又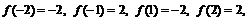

∴f(x)在[-2，2]上的最大值和最小值分别为-2，2.

又∵、，

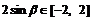∴. 故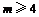，即m的最小值为4.

21．(1)由抛物线知焦点F(2，0)，准线l的方程为x= -2，若椭圆的中心为，长半轴长，短半轴长，半焦距分别为a, b, c，准线l与x轴交于点N，

则　　　　　　　　　　　 ①

设椭圆的短轴端点为B，且B的坐标为()，

BF的中点为，即，

又∵，代入①得，

它就是点M的轨迹方程.

(2)设为点M的轨迹上的一点，则　

令，其图象为开口向上的抛物线，对称轴为直线，由于为点M轨迹上的点，则x>2，于是当，即时，f(x)无最小值，|PQ|也无最小值，当m-1>2，即m>3时，　

∴当m>3时，