-
网址:http://m.1010jiajiao.com/paper/timu/5159516.html[举报]
10.定义在R上的函数
 满足
满足 ,且当
,且当 时,
时, .则
.则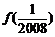 等于( )
等于( )A.
 B.
B. C.
C. D.
D.
第Ⅱ卷(非选择题,共100分)2,4,6
- 题目来源:08届高考理科数学第六次月考试题 数学试题(理科)2008年3月 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟. 第Ⅰ卷 (选择题 共50分)
08届高考理科数学第六次月考试题参考答案
一、选择题 ADDAA CADBC
|
11.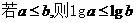 ; 12.7; 13.
; 12.7; 13. ; 14.
; 14. ; 15.①②; 16.
; 15.①②; 16. .
.
三、解答题:
17. ⑴

 ……………6分
……………6分
 的最大值为
的最大值为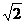 , 最小正周期
, 最小正周期 ……………8分
……………8分
⑵略。……………12分
18. 解:(1)设”可判断两个选项是错误的”两道题之一选对的为事件A,”有一道题可以判断一个选项是错误”选对的为事件为B,“有一道不理解题意”选对的为事件C,
 , ………..(3分)
, ………..(3分)
 得50分的概率为
得50分的概率为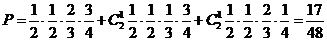 ; ……..(5分 )
; ……..(5分 )
得60分的概率为 .
……(7分)
.
……(7分)
(2)得40分概率为 ;
;
得45分的概率为 ;
;
得55分的概率为 .
……….(11分)
.
……….(11分)
所以 …………(13分)
…………(13分)
19.解: (1)取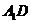 中点
中点 连接
连接
 ,则易证四边形
,则易证四边形 是矩形.所以
是矩形.所以 ,又
,又 所以
所以 . ………….(4分)
. ………….(4分)
(2)易算得, , ,
,
所以由余弦定理得 ,则
,则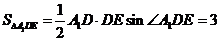 又
又 , …………(6分)
, …………(6分)
用等积法: ,得点A到平面
,得点A到平面 的距离为
的距离为 . ………….(8分)
. ………….(8分)
(3)取边 的中点P,连接PE,易知
的中点P,连接PE,易知 ,则
,则 是
是 在上的射影。
…………..(10分)
在上的射影。
…………..(10分)
计算得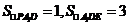 ,所以二面角
,所以二面角 的平面角
的平面角 的余弦值为
的余弦值为 ,
……………(12分)
,
……………(12分)
 .
……………(13分)
.
……………(13分)
20. 解:⑴定义域为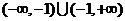 ,
,
因为 ……………..…(2分 )
……………..…(2分 )
所以,当 或
或 时,
时,
当 或
或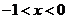 时,
时, …………………(4分)
…………………(4分)
故 的单调递增区间是
的单调递增区间是 和
和 ……………………
(5分)
……………………
(5分)
⑵由 得:
得: ,
,
令 ,
……………………(7分)
,
……………………(7分)
则 或
或
所以 ≤
≤ 时,
时, ≤
≤ 时,
时,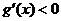
故 在
在 上递减,在
上递减,在 上递增
…………………..(9分)
上递增
…………………..(9分)
要使 在
在 恰有两相异实根,则必须且只需
恰有两相异实根,则必须且只需

则 ……………..(12分)
……………..(12分)
21.(1).设椭圆 的方程为
的方程为 ,则由题意得
,则由题意得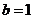 . ……..(2分)
. ……..(2分)
 ,即
,即 ,所以
,所以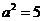 .
………………….(4分)
.
………………….(4分)
故椭圆 的方程为
的方程为 .
………………………….(5分)
.
………………………….(5分)
(2).设点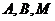 的坐标分别为
的坐标分别为 .
.
易知点 的坐标为
的坐标为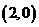 .
.

 ,则
,则
将点 的坐标代入到椭圆方程中,得
的坐标代入到椭圆方程中,得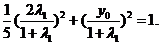
化简得 .
…………………………….…..(8分)
.
…………………………….…..(8分)
同理,由 得
得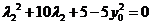 ,
,
所以, 是方程
是方程 的两个根,
…………….…..(11分)
的两个根,
…………….…..(11分)
 …………….…..(12分)
…………….…..(12分)
22.(1).当 时,
时,

所以,  ……………………(3分)
……………………(3分)
故 .
………………………(5分)
.
………………………(5分)
(2).当 时,
时, ,结论成立;
……………………..(6分)
,结论成立;
……………………..(6分)
当 时,
时,
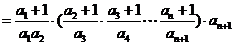 ……………………..(8分)
……………………..(8分)

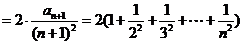
 …………………….(10分)
…………………….(10分)
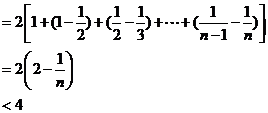
综上述,对任意 ,不等式成立.
………………………….(12分)
,不等式成立.
………………………….(12分)