-
网址:http://m.1010jiajiao.com/paper/timu/5154943.html[举报]
直线方程
[知识点]
1. 直线方程两点式:
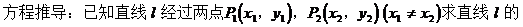
方程?
解:
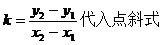

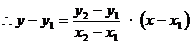

注意:(1)特殊情况:x=x1或y=y1不能用两点式表示,即与x轴平行或与x轴垂直的直线不能用两点式表示,故平面上的直线与两点式方程不是一一对应。
(2)两点式变形形式:(y-y1)(x2-x1)=(y2-y1)(x-x1)
此方程与平面上的直线一一对应。
- 题目来源:直线方程
[试题答案]
1. D
解析:在方程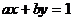 中
中
令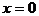 得
得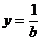 ;
;
令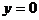 得
得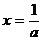 。
。
∴直线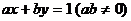 与两坐标轴围成的三角形面积是:
与两坐标轴围成的三角形面积是:
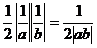
2. C
解析:设过点A(4,1)的直线的方程为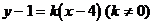
令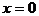 ,得
,得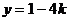 ;
;
令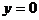 ,得
,得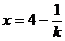 。
。
由已知得: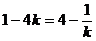
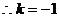 或
或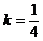
∴所求直线的方程为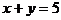 或
或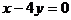 (此题也可用直线方程的截距式求,但需讨论)。
(此题也可用直线方程的截距式求,但需讨论)。
3. 解析:由条件知:A.B.C≠0
在方程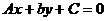 中,
中,
令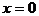 ,得
,得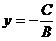 ;
;
令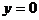 ,得
,得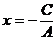
由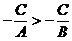 得:
得: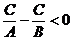
4. B
解析:由 得
得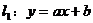
由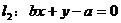 得
得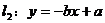
下面用排除法,在A选项中,由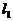 的图象知
的图象知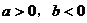 ,判断知
,判断知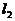 的图象不符合。
的图象不符合。
在B选项中,由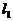 的图象知
的图象知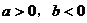 ,判断知
,判断知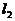 的图象符合,所以应选B。
的图象符合,所以应选B。
5. D
解析:在方程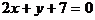 中分别令
中分别令 ,得:
,得:
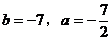
6. 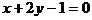
解析:∵直线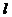 的倾斜角为
的倾斜角为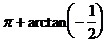
∴直线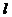 的斜率
的斜率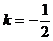 ,由点斜式得直线
,由点斜式得直线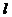 的方程为:
的方程为:
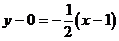 ,即
,即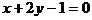
7. 分析:先根据已知条件写出直线的方程,再化成直线的斜截式方程。
解:(1)直线的两点式方程为:
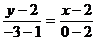
化为斜截式方程为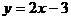
(2)直线截距式方程为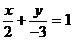
化为斜截式方程为
8. 解:(1)在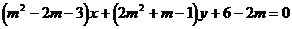 中,
中,
令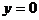 ,得
,得
由题意知: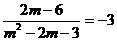
解得: (舍去)为所求。
(舍去)为所求。
(2)因为直线的斜率为1,所以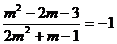
解得: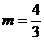 为所求(
为所求(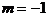 舍去)
舍去)
9. 解:设直线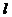 的方程为
的方程为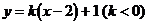
分别令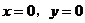 得:
得:
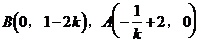
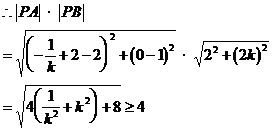
∵k<0,∴当且仅当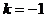 时,
时,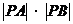 取得最小值4
取得最小值4
故所求直线的方程为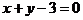
10. 解:设直线的截距式方程为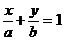
由题意得:
即 或
或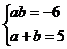
由 解得:
解得: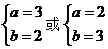
由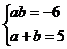 解得:
解得: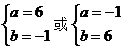
故所求直线有4条。
11. 解:∵直线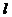 的纵截距为
的纵截距为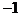
∴直线过点M(0,-1)
∵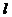 与线段PQ相交
与线段PQ相交
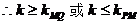
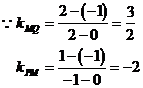
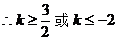
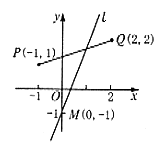
点评:由于直线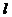 过定点M(0,-1),所以问题转化为过定点的直线与线段PQ相交。此类题可用数形结合法解决。在找边界时注意转动直线
过定点M(0,-1),所以问题转化为过定点的直线与线段PQ相交。此类题可用数形结合法解决。在找边界时注意转动直线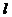 ,观察其倾斜角的变化。
,观察其倾斜角的变化。