精英家教网> 试卷> 高考数学二轮复习空间垂直与与平行证明
[考点聚焦]
考点1:空间元素点、线、面之间的垂直与平行关系的判断;
考点2:空间线面垂直与平行关系的证明;简单几何体中的线面关系证明;
[考点小测] > 题目详情
-
网址:http://m.1010jiajiao.com/paper/timu/5154850.html[举报]
1.已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面.给出下列的四个命题: ①若
 ,
,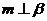 ,则
,则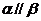 ;②若
;②若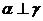 ,
,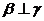 ,则
,则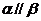 ;③若
;③若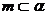 ,
,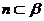 ,
,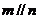 ,则
,则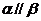 ;
;④若m、n是异面直线,
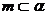 ,
,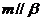 ,
,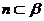 ,
, ,则
,则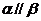 ,其中真命题是
,其中真命题是A.①和② B.①和③ C.③和④ D.①和④
- 题目来源:高考数学二轮复习空间垂直与与平行证明 [考点聚焦] 考点1:空间元素点、线、面之间的垂直与平行关系的判断; 考点2:空间线面垂直与平行关系的证明;简单几何体中的线面关系证明; [考点小测]