精英家教网> 试卷> 高考数学第二轮数学专题训练一
(理)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.共150分,考试时间为120分钟.
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(AB)=P(A)P(B)
如果事件A在一次试验中发生的概率是,那么次独立重复试验中恰好发生次的概率是
球的表面积公式、球的体积公式,其中表示球的半径
第I卷(选择题,共50分) > 题目详情
-
网址:http://m.1010jiajiao.com/paper/timu/5154747.html[举报]
20.(本小题满分13分)在平面直角坐标系中,已知A1
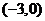 ,A2
,A2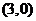 ,P(
,P(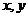 ),M
),M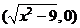 ,O为坐标原点,若实数
,O为坐标原点,若实数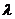 使向量
使向量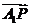 ,
,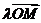 和
和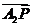 满足
满足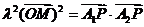 .
.(1)求点P的轨迹方程,并判断P点的轨迹是怎样的曲线;
(2)当
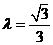 时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一个交点为B,能否在直线
时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一个交点为B,能否在直线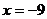 上找到一点C,恰使
上找到一点C,恰使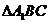 为正三角形?请说明理由.
为正三角形?请说明理由.[解答](1)由已知可得
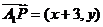 ,
,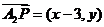 ,
,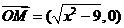 ,且
,且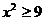 ,∴
,∴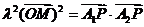 即
即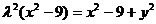 ,
,即点P的轨迹方程是
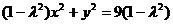 ,
,当
 即
即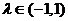 时,有
时,有 ,
,此时
 ,∴
,∴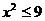 ,综合
,综合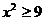 知此时点的轨迹即为两点A1和A2;
知此时点的轨迹即为两点A1和A2;当
 即
即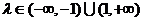 时,方程为
时,方程为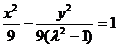 ,
,此时点P的轨迹是双曲线;
当
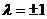 时,方程为
时,方程为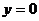 ,且
,且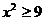 为两条射线;
为两条射线;(2)过点A1斜率为1的直线方程为
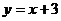 ,
,当
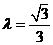 时,曲线方程为
时,曲线方程为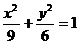 ,其轨迹就是两点A1和A2,
,其轨迹就是两点A1和A2,此时直线
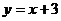 过点A1但不过A2点,∴B点不存在,从而这样的三角形也不存在.
过点A1但不过A2点,∴B点不存在,从而这样的三角形也不存在. - 题目来源:高考数学第二轮数学专题训练一 (理) 本试卷分第I卷(选择题)和第II卷(非选择题)两部分.共150分,考试时间为120分钟. 参考公式: 如果事件A、B互斥,那么P(A+B)=P(A)+P(B) 如果事件A、B相互独立,那么P(AB)=P(A)P(B) 如果事件A在一次试验中发生的概率是,那么次独立重复试验中恰好发生次的概率是 球的表面积公式、球的体积公式,其中表示球的半径 第I卷(选择题,共50分)