-
网址:http://m.1010jiajiao.com/paper/timu/5153859.html[举报]
19.(本小题满分13分)
已知双曲线
 的右焦点为
的右焦点为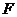 ,过点
,过点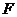 的动直线与双曲线相交于
的动直线与双曲线相交于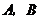 两点,点
两点,点 的坐标是
的坐标是 .
.(I)证明
 ,
,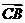 为常数;
为常数;(II)若动点
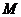 满足
满足 (其中
(其中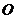 为坐标原点),求点
为坐标原点),求点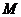 的轨迹方程.
的轨迹方程. - 题目来源:高考数学招生适应性考试试卷 数学(文史类)
高考数学招生适应性考试试卷
数学(文史类)参考答案
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.D 2.B 3.A 4.B 5.C 6.D 7.C 8.C 9.D 10.B
二、填空题:本大题共5小题,每小题5分,共25分.把答案填在横线上.
11.
12.
13.3
14.(1) (2)
(2)
15.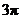 ,
,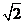
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16.解: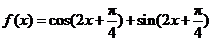
 .
.
(I)函数 的最小正周期是
的最小正周期是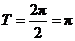 ;
;
(II)当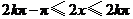 ,即
,即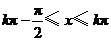 (
( )时,函数
)时,函数 是增函数,故函数
是增函数,故函数 的单调递增区间是
的单调递增区间是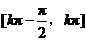 (
( ).
).
17.解:任选1名下岗人员,记“该人参加过财会培训”为事件 ,“该人参加过计算机培训”为事件
,“该人参加过计算机培训”为事件 ,由题设知,事件
,由题设知,事件 与
与 相互独立,且
相互独立,且 ,
,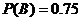 .
.
(I)解法一:任选1名下岗人员,该人没有参加过培训的概率是
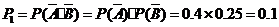
所以该人参加过培训的概率是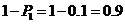 .
.
解法二:任选1名下岗人员,该人只参加过一项培训的概率是

该人参加过两项培训的概率是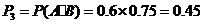 .
.
所以该人参加过培训的概率是 .
.
(II)解法一:任选3名下岗人员,3人中只有2人参加过培训的概率是
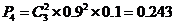 .
.
3人都参加过培训的概率是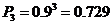 .
.
所以3人中至少有2人参加过培训的概率是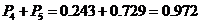 .
.
解法二:任选3名下岗人员,3人中只有1人参加过培训的概率是
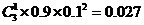 .
.
3人都没有参加过培训的概率是 .
.
所以3人中至少有2人参加过培训的概率是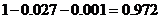 .
.
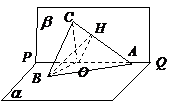 18.解:(I)在平面
18.解:(I)在平面 内过点
内过点 作
作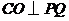 于点
于点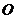 ,连结
,连结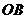 .
.
因为 ,
, ,所以
,所以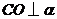 ,
,
又因为 ,所以
,所以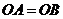 .
.
而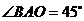 ,所以
,所以 ,
, ,从而
,从而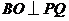 ,又
,又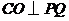 ,
,
所以 平面
平面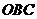 .因为
.因为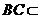 平面
平面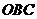 ,故
,故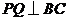 .
.
(II)解法一:由(I)知,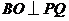 ,又
,又 ,
, ,
, ,所以
,所以 .
.
过点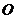 作
作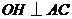 于点
于点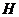 ,连结
,连结 ,由三垂线定理知,
,由三垂线定理知, .
.
故 是二面角
是二面角 的平面角.
的平面角.
由(I)知,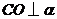 ,所以
,所以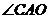 是
是 和平面
和平面 所成的角,则
所成的角,则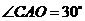 ,
,
不妨设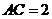 ,则
,则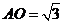 ,
,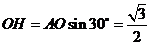 .
.
在 中,
中,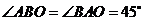 ,所以
,所以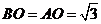 ,
,
于是在 中,
中, .
.
故二面角 的大小为
的大小为 .
.
解法二:由(I)知,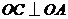 ,
, ,
, ,故可以
,故可以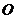 为原点,分别以直线
为原点,分别以直线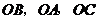 为
为 轴,
轴,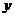 轴,
轴,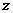 轴建立空间直角坐标系(如图).
轴建立空间直角坐标系(如图).
因为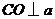 ,所以
,所以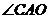 是
是 和平面
和平面 所成的角,则
所成的角,则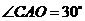 .
.
不妨设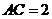 ,则
,则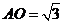 ,
, .
.
 在
在 中,
中,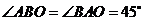 ,
,
所以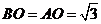 .
.
则相关各点的坐标分别是
 ,
, ,
,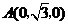 ,
,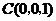 .
.
所以 ,
,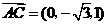 .
.
设
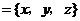 是平面
是平面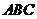 的一个法向量,由
的一个法向量,由 得
得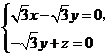
取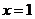 ,得
,得 .
.
易知 是平面
是平面 的一个法向量.
的一个法向量.
设二面角 的平面角为
的平面角为 ,由图可知,
,由图可知, .
.
所以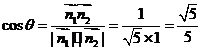 .
.
故二面角 的大小为
的大小为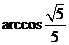 .
.
19.解:由条件知 ,设
,设 ,
,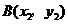 .
.
(I)当 与
与 轴垂直时,可设点
轴垂直时,可设点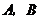 的坐标分别为
的坐标分别为 ,
, ,
,
此时 .
.
当 不与
不与 轴垂直时,设直线
轴垂直时,设直线 的方程是
的方程是 .
.
代入 ,有
,有 .
.
则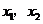 是上述方程的两个实根,所以
是上述方程的两个实根,所以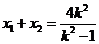 ,
,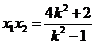 ,
,
于是


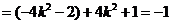 .
.
综上所述, 为常数
为常数 .
.
(II)解法一:设 ,则
,则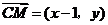 ,
,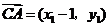 ,
,
 ,
,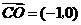 ,由
,由 得:
得:
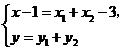 即
即
于是 的中点坐标为
的中点坐标为 .
.
当 不与
不与 轴垂直时,
轴垂直时,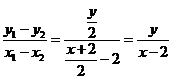 ,即
,即 .
.
又因为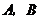 两点在双曲线上,所以
两点在双曲线上,所以 ,
, ,两式相减得
,两式相减得
 ,即
,即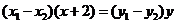 .
.
将 代入上式,化简得
代入上式,化简得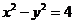 .
.
当 与
与 轴垂直时,
轴垂直时,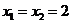 ,求得
,求得 ,也满足上述方程.
,也满足上述方程.
所以点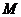 的轨迹方程是
的轨迹方程是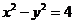 .
.
解法二:同解法一得 ……………………………………①
……………………………………①
当 不与
不与 轴垂直时,由(I) 有
轴垂直时,由(I) 有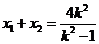 .…………………②
.…………………②
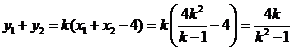 .………………………③
.………………………③
由①②③得 .…………………………………………………④
.…………………………………………………④
 .……………………………………………………………………⑤
.……………………………………………………………………⑤
当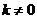 时,
时, ,由④⑤得,
,由④⑤得, ,将其代入⑤有
,将其代入⑤有
 .整理得
.整理得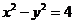 .
.
当 时,点
时,点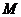 的坐标为
的坐标为 ,满足上述方程.
,满足上述方程.
当 与
与 轴垂直时,
轴垂直时,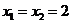 ,求得
,求得 ,也满足上述方程.
,也满足上述方程.
故点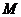 的轨迹方程是
的轨迹方程是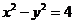 .
.
20.解:(I)当 时,由已知得
时,由已知得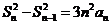 .
.
因为 ,所以
,所以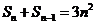 . …………………………①
. …………………………①
于是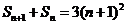 . …………………………………………………②
. …………………………………………………②
由②-①得: .……………………………………………③
.……………………………………………③
于是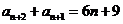 .……………………………………………………④
.……………………………………………………④
由④-③得: .…………………………………………………⑤
.…………………………………………………⑤
即数列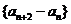 (
( )是常数数列.
)是常数数列.
(II)由①有 ,所以
,所以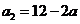 .
.
由③有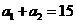 ,所以
,所以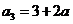 ,
,
而⑤表明:数列 和
和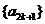 分别是以
分别是以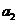 ,
, 为首项,6为公差的等差数列.
为首项,6为公差的等差数列.
所以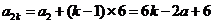 ,
, ,
, .
.
由题设知, .当
.当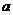 为奇数时,
为奇数时,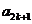 为奇数,而
为奇数,而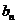 为偶数,所以
为偶数,所以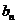 不是数列
不是数列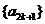 中的项,
中的项,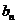 只可能是数列
只可能是数列 中的项.
中的项.
若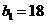 是数列
是数列 中的第
中的第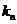 项,由
项,由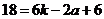 得
得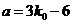 ,取
,取 ,得
,得 ,此时
,此时 ,由
,由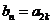 ,得
,得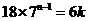 ,
,
 ,从而
,从而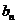 是数列
是数列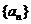 中的第
中的第 项.
项.
(注:考生取满足 ,
, 的任一奇数,说明
的任一奇数,说明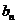 是数列
是数列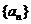 中的第
中的第 项即可)
项即可)
21.解:(I)因为函数 在区间
在区间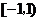 ,
,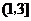 内分别有一个极值点,所以
内分别有一个极值点,所以
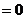 在
在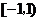 ,
,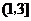 内分别有一个实根,
内分别有一个实根,
设两实根为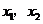 (
( ),则
),则 ,且
,且 .于是
.于是
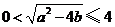 ,
, ,且当
,且当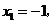
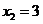 ,即
,即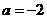 ,
,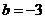 时等号成立.故
时等号成立.故 的最大值是16.
的最大值是16.
(II)解法一:由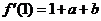 知
知 在点
在点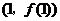 处的切线
处的切线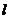 的方程是
的方程是
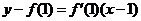 ,即
,即 ,
,
因为切线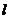 在点
在点 处空过
处空过 的图象,
的图象,
所以 在
在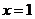 两边附近的函数值异号,则
两边附近的函数值异号,则
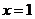 不是
不是 的极值点.
的极值点.
而
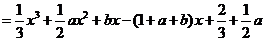 ,且
,且
 .
.
若 ,则
,则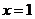 和
和 都是
都是 的极值点.
的极值点.
所以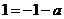 ,即
,即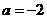 ,又由
,又由 ,得
,得 ,故
,故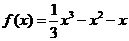 .
.
解法二:同解法一得
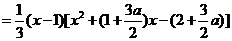 .
.
因为切线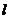 在点
在点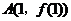 处穿过
处穿过 的图象,所以
的图象,所以 在
在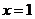 两边附近的函数值异号,于是存在
两边附近的函数值异号,于是存在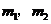 (
( ).
).
当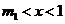 时,
时,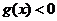 ,当
,当 时,
时,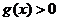 ;
;
或当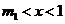 时,
时,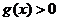 ,当
,当 时,
时,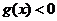 .
.
设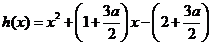 ,则
,则
当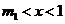 时,
时,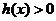 ,当
,当 时,
时,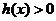 ;
;
或当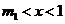 时,
时, ,当
,当 时,
时, .
.
由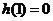 知
知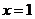 是
是 的一个极值点,则
的一个极值点,则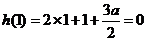 ,
,
所以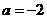 ,又由
,又由 ,得
,得 ,故
,故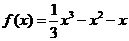 .
.