-
网址:http://m.1010jiajiao.com/paper/timu/5152336.html[举报]
19. (14分)对1个单位质量的含污物体进行清洗, 清洗前其清洁度(含污物体的清洁度定义为:
 为
为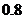 , 要求清洗完后的清洁度为
, 要求清洗完后的清洁度为 . 有两种方案可供选择, 方案甲: 一次清洗; 方案乙: 分两次清洗. 该物体初次清洗后受残留水等因素影响, 其质量变为
. 有两种方案可供选择, 方案甲: 一次清洗; 方案乙: 分两次清洗. 该物体初次清洗后受残留水等因素影响, 其质量变为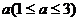 . 设用
. 设用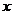 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是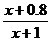
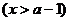 , 用
, 用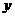 单位质量的水第二次清洗后的清洁度是
单位质量的水第二次清洗后的清洁度是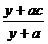 , 其中
, 其中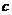
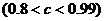 是该物体初次清洗后的清洁度.
是该物体初次清洗后的清洁度.(1)分别求出方案甲以及
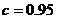 时方案乙的用水量, 并比较哪一种方案用水量较少;
时方案乙的用水量, 并比较哪一种方案用水量较少;(2)若采用方案乙, 当
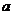 为某固定值时, 如何安排初次与第二次清洗的用水量, 使总用水量最小? 并讨论
为某固定值时, 如何安排初次与第二次清洗的用水量, 使总用水量最小? 并讨论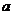 取不同数值时对最少总用水量多少的影响.
取不同数值时对最少总用水量多少的影响. - 题目来源:集合、逻辑联结词、函数(理科)高考备考建议 东莞中学 庞进发
参考答案
1.C 2. C 3.C
4.D 5.C 6.B 7.C
8.A 9. 6 10. 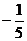
11. 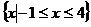 ;
;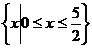 12. 4 13.
12. 4 13. 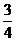 14. ①④⑤
14. ①④⑤
15. 解:由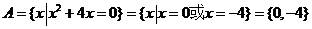 .
.
∵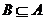 ,∴
,∴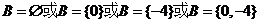 .
.
当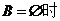 ,即
,即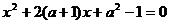 无实根,由
无实根,由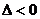 ,
,
即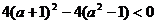 ,解得
,解得 ;
;
当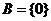 时,由根与系数的关系:
时,由根与系数的关系: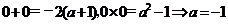 ;
;
当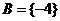 时,由根与系数的关系:
时,由根与系数的关系: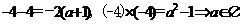 ;
;
当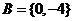 时,由根与系数的关系:
时,由根与系数的关系: ;
;
综上所得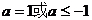 .
.
16. 解法一: (Ⅰ)由图象可知,在(-∞,1)上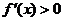 ,在(1,2)上
,在(1,2)上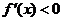 ,在
,在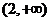 上
上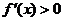 , 故
, 故 在
在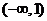 ,
,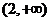 上递增,在(1,2)上递减,因此
上递增,在(1,2)上递减,因此 在
在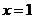 处取得极大值,所以
处取得极大值,所以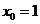 .
.
(Ⅱ)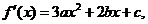 由
由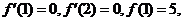 得
得 解得
解得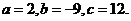
解法二:(Ⅰ)同解法一.
(Ⅱ)设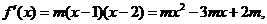
又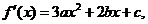 所以
所以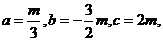
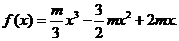
由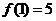 ,即
,即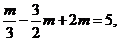 得
得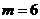 ,
所以
,
所以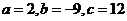 .
.
17. 解:(1) 当 时,
时, ,
,
则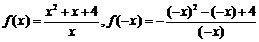
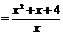
∴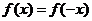 当
当 时,
时,  ,
,
则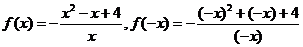
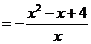 ,
,
∴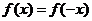
综上所述, 对于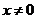 , 都有
, 都有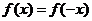 ,∴ 函数
,∴ 函数 是偶函数。
是偶函数。
(2)当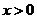 时,
时, 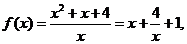
设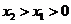 , 则
, 则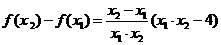 .
.
当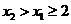 时,
时, 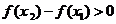 ;
;
当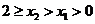 时,
时, 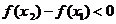 ,
,
∴ 函数 在
在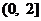 上是减函数, 函数
上是减函数, 函数 在
在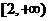 上是增函数。
上是增函数。
(3)由(2)知, 当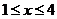 时,
时, 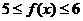 ,
,
又由(1)知, 函数 是偶函数, ∴ 当
是偶函数, ∴ 当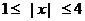 时,
时, 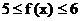 ,
,
∴若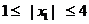 ,
,  , 则
, 则 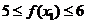 ,
, 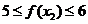 ,
,
∴ , 即
, 即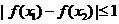 .
.
18.解:(1)因为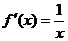 ,所以
,所以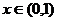 时,
时,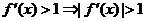 ,
,
即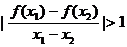 . 当
. 当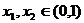 时,
时, ;
;
(2)由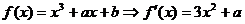 ,
,
当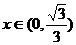 时,
时,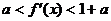 ,因为
,因为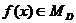 ,
,
所以 ,即
,即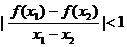 ;
;
所以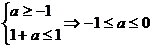 即为所求.
即为所求.
评析:本题应用常规解法,解答较为繁琐;若用导数的几何意义,则十分简单。
19. 解:(1)设方案甲与方案乙的用水量分别为x与z,由题设有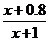 =0.99,解得x=19.
=0.99,解得x=19.
由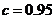 得方案乙初次用水量为3, 第二次用水量y满足方程:
得方案乙初次用水量为3, 第二次用水量y满足方程:
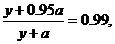 解得y=4
解得y=4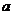 ,故z=4
,故z=4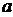 +3.即两种方案的用水量分别为19与4
+3.即两种方案的用水量分别为19与4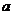 +3.
+3.
因为当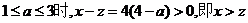 ,故方案乙的用水量较少.
,故方案乙的用水量较少.
(2)设初次与第二次清洗的用水量分别为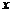 与
与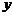 ,类似(I)得
,类似(I)得
 ,
,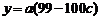 (*)
(*)
于是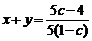 +
+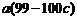

当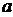 为定值时,
为定值时,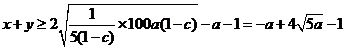 ,
,
当且仅当 时等号成立.此时
时等号成立.此时
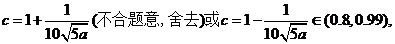
将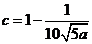 代入(*)式得
代入(*)式得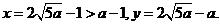
故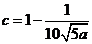 时总用水量最少, 此时第一次与第二次用水量分别为
时总用水量最少, 此时第一次与第二次用水量分别为
 , 最少总用水量是
, 最少总用水量是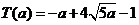 .
.
当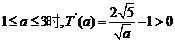 ,故T(
,故T(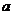 )是增函数(也可以用二次函数的单
)是增函数(也可以用二次函数的单
调性判断).这说明,随着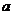 的值的最少总用水量, 最少总用水量最少总用水量.
的值的最少总用水量, 最少总用水量最少总用水量.
20. 解:(Ⅰ)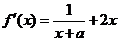 ,依题意有
,依题意有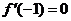 ,故
,故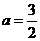 .
.
从而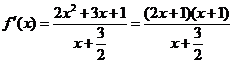 .
.
 的定义域为
的定义域为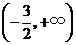 ,当
,当 时,
时,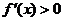 ;
;
当 时,
时,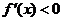 ;当
;当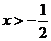 时,
时,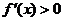 .
.
从而, 分别在区间
分别在区间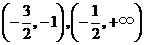 单调增加,在区间
单调增加,在区间 单调减少.
单调减少.
(Ⅱ) 的定义域为
的定义域为 ,
,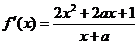 .
.
方程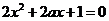 的判别式
的判别式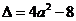 .
.
(ⅰ)若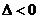 ,即
,即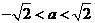 ,在
,在 的定义域内
的定义域内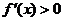 ,故
,故 的极值.
的极值.
(ⅱ)若 ,则
,则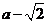 或
或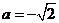 .
.
若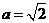 ,
,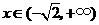 ,
,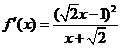 .
.
当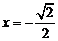 时,
时,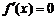 ,当
,当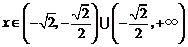 时,
时,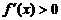 ,所以
,所以 无极值.
无极值.
若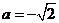 ,
,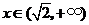 ,
,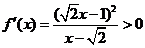 ,
, 也无极值.
也无极值.
(ⅲ)若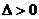 ,即
,即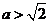 或
或 ,则
,则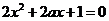 有两个不同的实根
有两个不同的实根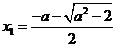 ,
,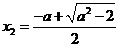 .
.
当 时,
时,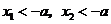 ,从而
,从而 有
有 的定义域内没有零点,故
的定义域内没有零点,故 无极值.
无极值.
当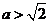 时,
时,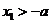 ,
,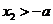 ,
, 在
在 的定义域内有两个不同的零点,由根值判别方法知
的定义域内有两个不同的零点,由根值判别方法知 在
在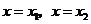 取得极值.
取得极值.
综上, 存在极值时,
存在极值时,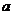 的取值范围为
的取值范围为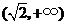 .
.
 的极值之和为
的极值之和为
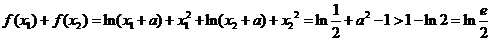 .
.