-
网址:http://m.1010jiajiao.com/paper/timu/5151839.html[举报]
9、如图所示是2008年北京奥运会的会徽,其中的“中国印”由四个色块构成,可以用线段在不穿越其他色块的条件下将其中任意两个色块连接起来(如同架桥),如果用三条线段将这四个色块连接起来,不同的连接方法共有( )

A.8种 B.12种 C.16种 D.20种
- 题目来源:江苏省东海高级中学2007届 高考数学仿真试题一 本试卷分第Ⅰ卷(选择题 共50分)和第Ⅱ卷(非选择题 共100分),考试时间为120分钟,满分为150分. 第Ⅰ卷(选择题 共50分)
答 案
一、选择题:DABCD AAACB
二、填空题
11. 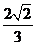 ;12. [1,5]; 13.6
;12. [1,5]; 13.6 ;14. (0,
;14. (0,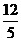 ] ; 15、4;16.① ④.
] ; 15、4;16.① ④.
三、解答题
17.解(1)∵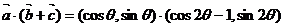
 ……………………………
3分
……………………………
3分
=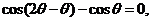
∴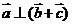 ……………………………………………………………………6分
……………………………………………………………………6分
(2)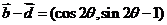 ………………………………………………………7分
………………………………………………………7分
 …………………9分
…………………9分
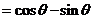 =
=
∵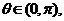 ∴
∴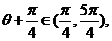 ∴
∴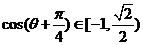
∴ 的值域为
的值域为 ……………………12分
……………………12分
18.(本小题满分14分)
解:(1)设 ,则以AB为直径的圆恰好过原点O的充要条件是
,则以AB为直径的圆恰好过原点O的充要条件是 ,即
,即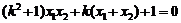 …①……2分
…①……2分
由 消去y得
消去y得 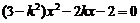 …②
…②
 …………………………5分
…………………………5分
将其代入①得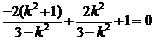 ,解得
,解得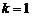 或
或
当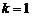 时,方程②为
时,方程②为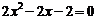 ,有两个不等实根;
,有两个不等实根;
当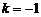 时,方程②为
时,方程②为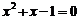 ,有两个不等实根.
,有两个不等实根.
故当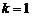 或
或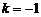 时,以AB为直径的圆恰好过原点O. ………………8分
时,以AB为直径的圆恰好过原点O. ………………8分
(2)若 关于直线
关于直线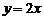 对称,
对称,
则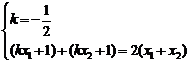 …………………………10分
…………………………10分
将④整理得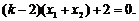 ………………12分
………………12分
因为 所以
所以 ,解之,得
,解之,得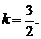 这个结果与③矛盾.
这个结果与③矛盾.
故不存在这样的k,使两点A、B关于直线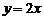 对称. ……………………14分
对称. ……………………14分
18.解:(I)设P(x,y),因为A、B分别为直线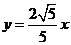 和
和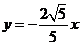 上的点,故可设
上的点,故可设 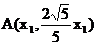 ,
,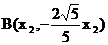 .
.
∵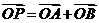 ,
,
∴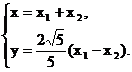 ∴
∴ ………………………4分
………………………4分
又 ,
,
∴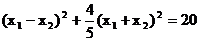 .……………………………………5分
.……………………………………5分
∴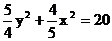 .
.
即曲线C的方程为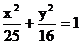 .………………………………………6分
.………………………………………6分
(II) 设N(s,t),M(x,y),则由 ,可得(x,y-16)=
,可得(x,y-16)= (s,t-16).
(s,t-16).
故 ,
,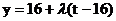 .……………………………………8分
.……………………………………8分
∵M、N在曲线C上,
∴ ……………………………………9分
……………………………………9分
消去s得 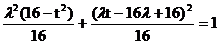 .
.
由题意知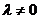 ,且
,且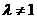 ,
,
解得  .………………………………………………………12分
.………………………………………………………12分
又 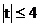 , ∴
, ∴ .
.
解得 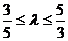 (
(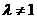 ).
).
故实数 的取值范围是
的取值范围是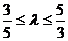 (
(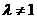 ).………………………………14分
).………………………………14分
19.解:(1) ∵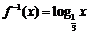 (
(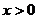 ), ………
2分
), ………
2分
∴ ,由题知,
,由题知, 恒成立,
恒成立,
∴10当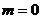 时,
时,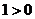 满足题意; ………
3分
满足题意; ………
3分
20当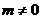 时,应有
时,应有 ,
,
∴实数 的取值范围为
的取值范围为 。 ……… 5分
。 ……… 5分
(2) ∵ 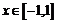 ,∴
,∴ ,
,

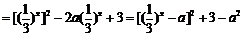 ,……… 7分
,……… 7分
当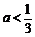 时,
时, ;
;
当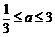 时,
时, ;
;
当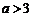 时,
时, .
.
∴
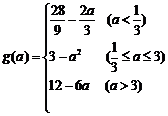 .
…………10分 (错一个扣一分)
.
…………10分 (错一个扣一分)
(3) ∵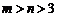 ,∴
,∴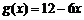 ,在
,在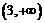 上是减函数.
上是减函数.
∵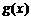 的定义域为
的定义域为 ,值域为
,值域为 ,
,
∴
 ,
, 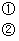 …………… 12分
…………… 12分
②-①得: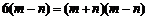 ,
,
∵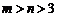 ,∴
,∴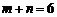 .但这与“
.但这与“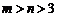 ”矛盾.
”矛盾.
∴满足题意的 、
、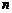 不存在.
………………… 14分
不存在.
………………… 14分
21.解:(1)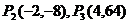 …………………………………………4分
…………………………………………4分
(2)曲线C上点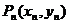 处的切线
处的切线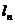 的斜率为
的斜率为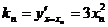 ,
,
故得到切线的方程为 ……………………………………6分
……………………………………6分
联立方程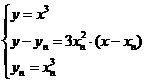 消去y,
消去y,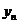 得:
得:
化简得: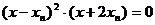 所以:
所以: ………………8分
………………8分
由 得到点Pn的坐标
得到点Pn的坐标 由
由 就得到点
就得到点 的坐标
的坐标 所以:
所以: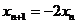 故数列
故数列 为首项为1,公比为-2的等比数列所以:
为首项为1,公比为-2的等比数列所以: …………………………………………10分
…………………………………………10分
(3)由(2)知: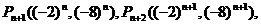
所以直线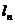 的方程为:
的方程为: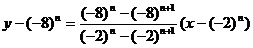
化简得: …………………………………………12分
…………………………………………12分
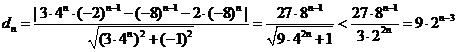
所以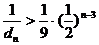 ∴
∴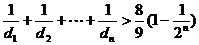 ≥
≥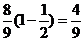 ……16分
……16分