-
1.命题
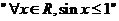 的否定是______________________.
的否定是______________________. -
2.cos43°cos77°+sin43°cos167°的值为 .
-
3.设
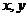 为实数,且
为实数,且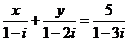 ,则
,则 _______.
_______. -
4. 已知向量
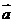 与
与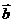 的夹角为
的夹角为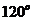 ,
,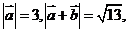 则
则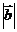 =_______.
=_______. -
5.若椭圆
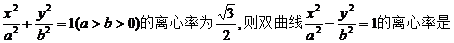 _____.
_____. -
6. 正方体的内切球与其外接球的体积之比为____________.
-
7.已知-7,
 ,
,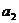 ,-1四个实数成等差数列,-4,
,-1四个实数成等差数列,-4,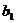 ,
,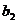 ,
,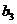 ,-1五个实数成等比数列,则
,-1五个实数成等比数列,则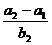 =__________.
=__________. -
8.若以连续掷两次骰子分别得到的点数m、n作为点P的横、纵坐标,则点P在直线x+y=5
下方的概率是________.
-
9. .已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是________________.
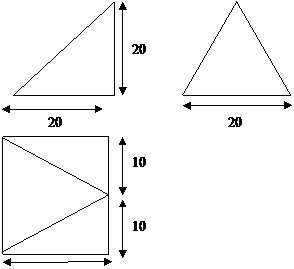
-
10.
 已知等差数列
已知等差数列 的前
的前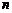 项和为
项和为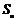 ,若
,若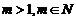 ,且
,且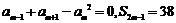 ,则
,则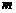 等于_____________.
等于_____________. -
11.一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图)。为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在
 (元)月收入段应抽出____人.
(元)月收入段应抽出____人. -
12.如果执行右图的程序框图,那么输出的S=

-
13.函数
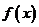 对于任意
对于任意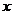 满足
满足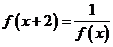 ,若
,若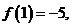 则
则 ______.
______. -
14.与直线
 和曲线
和曲线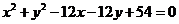 都相的切的半径最小圆的标准方程是__________________________.
都相的切的半径最小圆的标准方程是__________________________. -
15. 在△ABC中,a,b,c分别是角A,B,C的对边,且8sin2

(I)求角A的大小;(6分)
(II) 若a=
 ,b+c=3,求b和c的值(6分)
,b+c=3,求b和c的值(6分)
-
16.如图ABCD-A1B1C1D1是正四棱柱.(Ⅰ)求证:BD⊥平面ACC1A1; (6分) (Ⅱ)若二面角C1-BD-C为60o,求异面直线BC1与AC所成角余弦值(6分)
-
17.某厂家拟在2008年元旦节期间举行促销活动,经调查计算,该产品年销量(即该厂的年产量)x万件与年促销费用m万元(m
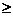 0)满足
0)满足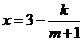 (k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2008年生产该产品的固定投入为8万元,每生产1万件产品需投入16万元,厂家每件产品的销售价格定为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分资金)
(k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2008年生产该产品的固定投入为8万元,每生产1万件产品需投入16万元,厂家每件产品的销售价格定为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分资金)(1)将2008年该产品的利润y万元表示为年销售费用m万元的函数;(8分)
(2)该厂家2008年的促销费用投入多少万元时,厂家的年利润最大?(6分)
-
18.
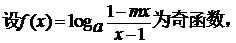

( a>1,且
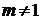 )
)(1) 求m 值 (4分) (2) 求g(x)的定义域
 (6分)
(6分)(3) 若g(x)在
 上恒正,求a的取值范围(6分)
上恒正,求a的取值范围(6分) -
19.已知抛物线
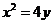 的焦点为F,A、B是抛物线上的两动点,且
的焦点为F,A、B是抛物线上的两动点,且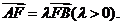 过A、B两点分别作抛物线的切线,设其交点为M。
过A、B两点分别作抛物线的切线,设其交点为M。(I)证明
 为定值;(10分)
为定值;(10分)(II)设
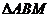 的面积为S,写出
的面积为S,写出 的表达式,并求S的最小值.(8分)
的表达式,并求S的最小值.(8分) -
20. 已知数列
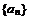 满足
满足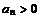 ,且对一切
,且对一切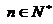 有
有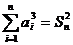 ,其中
,其中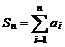 ,
, (Ⅰ)求证对一切
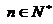 有
有 ,并求数列
,并求数列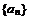 的通项公式;(6分)
的通项公式;(6分)(Ⅱ)记
 ,求数列
,求数列 的前
的前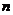 项和
项和 ;(6分)
;(6分)⑶求证
 . (6分)
. (6分)
08高考数学模拟试卷(三) 班级 姓名 成绩 参考答案
参考答案
一、填空题:(70分)
1.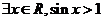 2.
2. 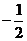 3.4
4.4 5.
3.4
4.4 5. 6.
6.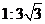 7.-1 8.
7.-1 8.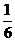 9.
9.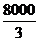 10.10 11.25
12.2550 13.
10.10 11.25
12.2550 13. 14.
14.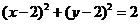
二、解答题
15.(I)在△ABC中有B+C=π-A,由条件可得:
4[1-cos(B+C)] -4cos2A+2=7
又∵cos(B+C)= -cosA
∴4cos2A-4cosA+1=0
解得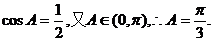
解: (II)由
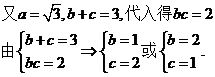
16. (Ⅰ)∵ABCD-A1B1C1D1是正四棱柱,∴CC1⊥平面ADCD, ∴BD⊥CC1
 ∵ABCD是正方形 ∴BD⊥AC
又∵AC,CC1
∵ABCD是正方形 ∴BD⊥AC
又∵AC,CC1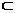 平面ACC1A1,
平面ACC1A1,
且AC∩CC1=C, ∴BD⊥平面ACC1A1.
(Ⅱ) 设BD与AC相交于O,连接C1O. ∵CC1⊥平面ADCD, ∴BD⊥AC,
∴BD⊥C1O, ∴∠C1OC∠是二面角C1-BD-C的平面角,
∴∠C1OC=60o. 连接A1B. ∵A1C1//AC, ∴∠A1C1B是BC1与AC所成的角.
设BC=a,则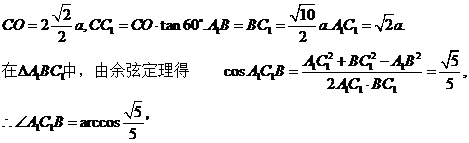 ∴异面直线BC1与AC所成角的大小为
∴异面直线BC1与AC所成角的大小为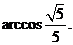
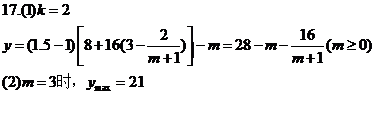
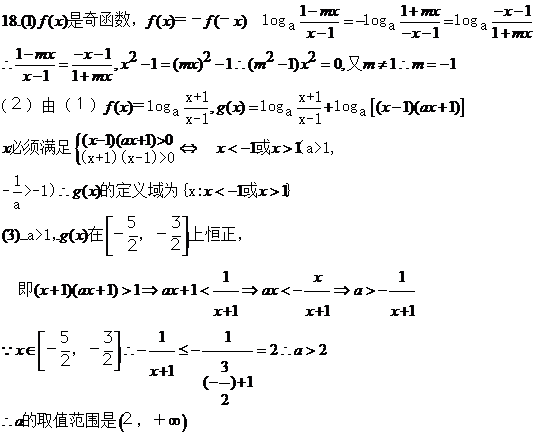
19. 解:(Ⅰ)由已知条件,得F(0,1),λ>0.
设A(x1,y1),B(x2,y2).由=λ,
即得 (-x1,1-y)=λ(x2,y2-1),
将①式两边平方并把y1=x12,y2=x22代入得 y1=λ2y2 ③
解②、③式得y1=λ,y2=,且有x1x2=-λx22=-4λy2=-4,
抛物线方程为y=x2,求导得y′=x.
所以过抛物线上A、B两点的切线方程分别是
y=x1(x-x1)+y1,y=x2(x-x2)+y2,
即y=x1x-x12,y=x2x-x22.
解出两条切线的交点M的坐标为(,)=(,-1). ……4分
所以.=(,-2).(x2-x1,y2-y1)=(x22-x12)-2(x22-x12)=0
所以.为定值,其值为0. ……7分
(Ⅱ)由(Ⅰ)知在△ABM中,FM⊥AB,因而S=|AB||FM|.
|FM|==
=
==+.
因为|AF|、|BF|分别等于A、B到抛物线准线y=-1的距离,所以
|AB|=|AF|+|BF|=y1+y2+2=λ++2=(+)2.
于是 S=|AB||FM|=(+)3,
由+≥2知S≥4,且当λ=1时,S取得最小值4.
20. (Ⅰ)由ni=1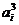 =Sn2,
(1) 由n+1i=1
=Sn2,
(1) 由n+1i=1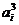 =Sn+12,
(2)
=Sn+12,
(2)
(2)-(1),得 =(Sn+1+Sn)(Sn+1-Sn)=(2 Sn+an+1) an+1.
=(Sn+1+Sn)(Sn+1-Sn)=(2 Sn+an+1) an+1.
∵ an+1 >0,∴an+12-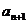 =2Sn.
=2Sn.
由an+12-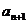 =2Sn,及an2-an =2Sn-1 (n≥2),
=2Sn,及an2-an =2Sn-1 (n≥2),
两式相减,得(an+1+ an)( an+1-an)= an+1+ an.
∵an+1+ an >0,∴an+1-an =1(n≥2)
当n=1,2时,易得a1=1,a2=2,∴an+1 - an =1(n≥1).
∴{ an}成等差数列,首项a1=1,公差d=1,故an=n .
(Ⅱ)由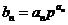 ,得
,得 。所以
。所以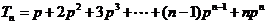 ,
,
当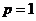 时,
时,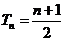 ;
;
当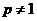 时,
时,
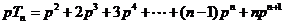 ,
,
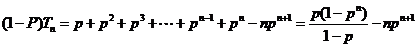
即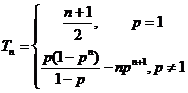
(Ⅲ)nk=1 =nk=1
=nk=1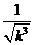 <1+nk=2
<1+nk=2
<1+nk=2=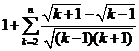
=1+ nk=2 (-)
=1+1+ -
- -<2+
-<2+ <3.
<3.