-
1.()y=esinxcos(sinx),则y′(0)等于( )
A.0 B.1 C.-1 D.2
-
2.()经过原点且与曲线y=
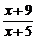 相切的方程是( )
相切的方程是( )A.x+y=0或
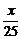 +y=0 B.x-y=0或
+y=0 B.x-y=0或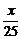 +y=0
+y=0C.x+y=0或
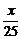 -y=0 D.x-y=0或
-y=0 D.x-y=0或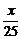 -y=0
-y=0 -
3.()若f′(x0)=2,
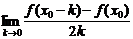 =_________.
=_________. -
4.()设f(x)=x(x+1)(x+2)…(x+n),则f′(0)=_________.
-
5.()已知曲线C1:y=x2与C2:y=-(x-2)2,直线l与C1、C2都相切,求直线l的方程.
-
6.()求函数的导数
(1)y=(x2-2x+3)e2x;
(2)y=
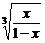 .
. -
7.()有一个长度为5 m的梯子贴靠在笔直的墙上,假设其下端沿地板以3 m/s的速度离开墙脚滑动,求当其下端离开墙脚1.4 m时,梯子上端下滑的速度.
-
8.()求和Sn=12+22x+32x2+…+n2xn-1,(x≠0,n∈N*).
难点34 导数的运算法则及基本公式应用 导数是中学限选内容中较为重要的知识,本节内容主要是在导数的定义,常用求等公式.四则运算求导法则和复合函数求导法则等问题上对考生进行训练与指导. ●难点磁场 ()已知曲线C:y=x3-3x2+2x,直线l:y=kx,且l与C切于点(x0,y0)(x0≠0),求直线l的方程及切点坐标. ●案例探究 [例1]求函数的导数: 命题意图:本题3个小题分别考查了导数的四则运算法则,复合函数求导的方法,以及抽象函数求导的思想方法.这是导数中比较典型的求导类型,属参考答案
参考答案
难点磁场
解:由l过原点,知k=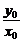 (x0≠0),点(x0,y0)在曲线C上,y0=x03-3x02+2x0,
(x0≠0),点(x0,y0)在曲线C上,y0=x03-3x02+2x0,
∴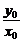 =x02-3x0+2
=x02-3x0+2
y′=3x2-6x+2,k=3x02-6x0+2
又k=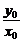 ,∴3x02-6x0+2=x02-3x0+2
,∴3x02-6x0+2=x02-3x0+2
2x02-3x0=0,∴x0=0或x0=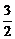
由x≠0,知x0=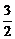
∴y0=(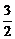 )3-3(
)3-3(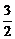 )2+2.
)2+2.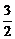 =-
=-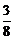
∴k=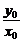 =-
=-
∴l方程y=- x 切点(
x 切点(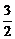 ,-
,-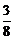 )
)
歼灭难点训练
一、1.解析:y′=esinx[cosxcos(sinx)-cosxsin(sinx)],y′(0)=e0(1-0)=1
答案:B
2.解析:设切点为(x0,y0),则切线的斜率为k=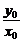 ,另一方面,y′=(
,另一方面,y′=(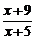 )′=
)′=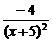 ,故
,故
y′(x0)=k,即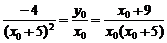 或x02+18x0+45=0得x0(1)=-3,y0(2)=-15,对应有y0(1)=3,y0(2)=
或x02+18x0+45=0得x0(1)=-3,y0(2)=-15,对应有y0(1)=3,y0(2)=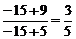 ,因此得两个切点A(-3,3)或B(-15,
,因此得两个切点A(-3,3)或B(-15, ),从而得y′(A)=
),从而得y′(A)=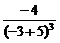 =-1及y′(B)=
=-1及y′(B)= 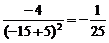 ,由于切线过原点,故得切线:lA:y=-x或lB:y=-
,由于切线过原点,故得切线:lA:y=-x或lB:y=-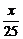 .
.
答案:A
二、3.解析:根据导数的定义:f′(x0)=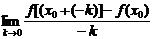 (这时
(这时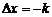 )
)
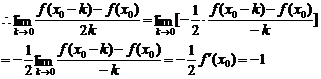
答案:-1
4.解析:设g(x)=(x+1)(x+2)……(x+n),则f(x)=xg(x),于是f′(x)=g(x)+xg′(x),f′(0)=g(0)+0.g′(0)=g(0)=1.2.…n=n!
答案:n!
三、5.解:设l与C1相切于点P(x1,x12),与C2相切于Q(x2,-(x2-2)2)
对于C1:y′=2x,则与C1相切于点P的切线方程为
y-x12=2x1(x-x1),即y=2x1x-x12 ①
对于C2:y′=-2(x-2),与C2相切于点Q的切线方程为y+(x2-2)2=-2(x2-2)(x-x2),即y=-2(x2-2)x+x22-4 ②
∵两切线重合,∴2x1=-2(x2-2)且-x12=x22-4,解得x1=0,x2=2或x1=2,x2=0
∴直线l方程为y=0或y=4x-4
6.解:(1)注意到y>0,两端取对数,得
lny=ln(x2-2x+3)+lne2x=ln(x2-2x+3)+2x
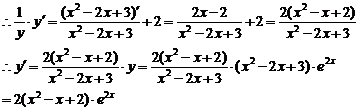
(2)两端取对数,得
ln|y|= (ln|x|-ln|1-x|),
(ln|x|-ln|1-x|),
两边解x求导,得

7.解:设经时间t秒梯子上端下滑s米,则s=5-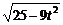 ,当下端移开1.4 m时,t0=
,当下端移开1.4 m时,t0=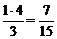 ,又s′=-
,又s′=-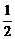 (25-9t2)
(25-9t2)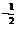 .(-9.2t)=9t
.(-9.2t)=9t ,所以s′(t0)=9×
,所以s′(t0)=9×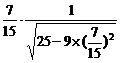 =0.875(m/s)
=0.875(m/s)
8.解:(1)当x=1时,Sn=12+22+32+…+n2=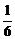 n(n+1)(2n+1),当x≠1时,1+2x+3x2+…+nxn-1=
n(n+1)(2n+1),当x≠1时,1+2x+3x2+…+nxn-1= ,两边同乘以x,得
,两边同乘以x,得
x+2x2+3x2+…+nxn= 两边对x求导,得
两边对x求导,得
Sn=12+22x2+32x2+…+n2xn-1
=