-
1.()已知A、B、C三点在曲线y=
 上,其横坐标依次为1,m,4(1<m<4),当△ABC的面积最大时,m等于( )
上,其横坐标依次为1,m,4(1<m<4),当△ABC的面积最大时,m等于( )A.3 B.
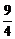 C.
C.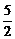 D.
D.
-
2.()设u,v∈R,且|u|≤
 ,v>0,则(u-v)2+(
,v>0,则(u-v)2+(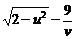 )2的最小值为( )
)2的最小值为( )A.4 B.2 C.8 D.2

-
3.()A是椭圆长轴的一个端点,O是椭圆的中心,若椭圆上存在一点P,使
∠OPA=
 ,则椭圆离心率的范围是_________.
,则椭圆离心率的范围是_________. -
4.()一辆卡车高3米,宽1.6米,欲通过抛物线形隧道,拱口宽恰好是抛物线的通径长,若拱口宽为a米,则能使卡车通过的a的最小整数值是_________.
-
5.()已知抛物线y=x2-1上一定点B(-1,0)和两个动点P、Q,当P在抛物线上运动时,BP⊥PQ,则Q点的横坐标的取值范围是_________.
-
6.()已知直线y=kx-1与双曲线x2-y2=1的左支交于A、B两点,若另一条直线l经过点P(-2,0)及线段AB的中点Q,求直线l在y轴上的截距b的取值范围.
-
7.()已知抛物线C:y2=4x.
(1)若椭圆左焦点及相应的准线与抛物线C的焦点F及准线l分别重合,试求椭圆短轴端点B与焦点F连线中点P的轨迹方程;
(2)若M(m,0)是x轴上的一定点,Q是(1)所求轨迹上任一点,试问|MQ|有无最小值?若有,求出其值;若没有,说明理由.
-
8.
 ()如图,
()如图, 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线l与曲线C相交于不同的两点M、N,且M在D、N之间,设
 =λ,求λ的取值范围.
=λ,求λ的取值范围.[学法指导]怎样学好圆锥曲线
圆锥曲线将几何与代数进行了完美结合.借助纯代数的解决手段研究曲线的概念和性质及直线与圆锥曲线的位置关系,从数学家笛卡尔开创了坐标系那天就已经开始.
高考中它依然是重点,主客观题必不可少,易、中、难题皆有.为此需要我们做到:
-
1.重点掌握椭圆、双曲线、抛物线的定义和性质.这些都是圆锥曲线的基石,高考中的题目都涉及到这些内容.
-
2.重视求曲线的方程或曲线的轨迹,此处作为高考解答题的命题对象难度较大.所以要掌握住一般方法:定义法、直接法、待定系数法、相关点法、参数法等.
-
3.加强直线与圆锥曲线的位置关系问题的复习.此处一直为高考的热点.这类问题常涉及到圆锥曲线的性质和直线的基本知识点、线段的中点、弦长、垂直问题,因此分析问题时利用数形结合思想和设而不求法与弦长公式及韦达定理联系去解决.这样加强了对数学各种能力的考查.
-
4.重视对数学思想、方法进行归纳提炼,达到优化解题思维、简化解题过程.
(1)方程思想
解析几何的题目大部分都以方程形式给定直线和圆锥曲线,因此把直线与圆锥曲线相交的弦长问题利用韦达定理进行整体处理,就简化解题运算量.
(2)用好函数思想方法
对于圆锥曲线上的一些动点,在变化过程中会引入一些相互联系、相互制约的量,从而使一些线的长度及a,b,c,e之间构成函数关系,函数思想在处理这类问题时就很有效.
(3)掌握坐标法
坐标法是解决有关圆锥曲线问题的基本方法.近几年都考查了坐标法,因此要加强坐标法的训练.
难点25 圆锥曲线综合题 圆锥曲线的综合问题包括:解析法的应用,与圆锥曲线有关的定值问题、最值问题、参数问题、应用题和探索性问题,圆锥曲线知识的纵向联系,圆锥曲线知识和三角、复数等代数知识的横向联系,解答这部分试题,需要较强的代数运算能力和图形认识能力,要能准确地进行数与形的语言转换和运算,推理转换,并在运算过程中注意思维的严密性,以保证结果的完整. ●难点磁场 ()若椭圆=1(a>b>0)与直线l:x+y=1在第一象限内有两个不同的交点,求a、b所满足的条件,并画出点P(a,b)的存在区域. 参考答案
参考答案
难点磁场
解:由方程组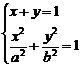 消去y,整理得(a2+b2)x2-2a2x+a2(1-b2)=0 ①
消去y,整理得(a2+b2)x2-2a2x+a2(1-b2)=0 ①
则椭圆与直线l在第一象限内有两个不同的交点的充要条件是方程①在区间(0,1)内有两相异实根,令f(x)=(a2+b2)x2-2a2x+a2(1-b2),则有

同时满足上述四个条件的点P(a,b)的存在区域为下图所示的阴影部分:
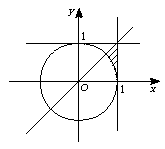
歼灭难点训练
一、1.解析:由题意知A(1,1),B(m, ),C(4,2).
),C(4,2).
直线AC所在方程为x-3y+2=0,
点B到该直线的距离为d= .
.

∵m∈(1,4),∴当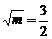 时,S△ABC有最大值,此时m=
时,S△ABC有最大值,此时m=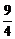 .
.
答案:B
2.解析:考虑式子的几何意义,转化为求圆x2+y2=2上的点与双曲线xy=9上的点的距离的最小值.
答案:C
二、3.解析:设椭圆方程为 =1(a>b>0),以OA为直径的圆:x2-ax+y2=0,两式联立消y得
=1(a>b>0),以OA为直径的圆:x2-ax+y2=0,两式联立消y得 x2-ax+b2=0.即e2x2-ax+b2=0,该方程有一解x2,一解为a,由韦达定理x2=
x2-ax+b2=0.即e2x2-ax+b2=0,该方程有一解x2,一解为a,由韦达定理x2= -a,0<x2<a,即0<
-a,0<x2<a,即0< -a<a
-a<a <e<1.
<e<1.
答案: <e<1
<e<1
4.解析:由题意可设抛物线方程为x2=-ay,当x= 时,y=-
时,y=- ;当x=0.8时,y=-
;当x=0.8时,y=- .由题意知
.由题意知 ≥3,即a2-12a-2.56≥0.解得a的最小整数为13.
≥3,即a2-12a-2.56≥0.解得a的最小整数为13.
答案:13
5.解析:设P(t,t2-1),Q(s,s2-1)
∵BP⊥PQ,∴ =-1,
=-1,
即t2+(s-1)t-s+1=0
∵t∈R,∴必须有Δ=(s-1)2+4(s-1)≥0.即s2+2s-3≥0,
解得s≤-3或s≥1.
答案:(-∞,-3 ∪
∪ 1,+∞)
1,+∞)
三、6.解:设A(x1,y1),B(x2,y2).
由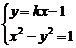 ,得(1-k2)x2+2kx-2=0,
,得(1-k2)x2+2kx-2=0,
又∵直线AB与双曲线左支交于A、B两点,
故有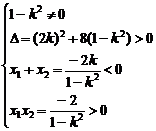
解得- <k<-1
<k<-1

7.解:由抛物线y2=4x,得焦点F(1,0),准线l:x=-1.
(1)设P(x,y),则B(2x-1,2y),椭圆中心O′,则|FO′|∶|BF|=e,又设点B到l的距离为d,则|BF|∶d=e,∴|FO′|∶|BF|=|BF|∶d,即(2x-2)2+(2y)2=2x(2x-2),化简得P点轨迹方程为y2=x-1(x>1).
(2)设Q(x,y),则|MQ|=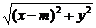

(ⅰ)当m- ≤1,即m≤
≤1,即m≤ 时,函数t=[x-(m-
时,函数t=[x-(m- )2]+m-
)2]+m-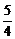 在(1,+∞)上递增,故t无最小值,亦即|MQ|无最小值.
在(1,+∞)上递增,故t无最小值,亦即|MQ|无最小值.
(ⅱ)当m- >1,即m>
>1,即m> 时,函数t=[x2-(m-
时,函数t=[x2-(m- )2]+m-
)2]+m-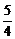 在x=m-
在x=m- 处有最小值m-
处有最小值m-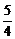 ,∴|MQ|min=
,∴|MQ|min= .
.
8.解:(1)以AB、OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系,
∵|PA|+|PB|=|QA|+|QB|=2 >|AB|=4.
>|AB|=4.
∴曲线C为以原点为中心,A、B为焦点的椭圆.
设其长半轴为a,短半轴为b,半焦距为c,则2a=2 ,∴a=
,∴a= ,c=2,b=1.
,c=2,b=1.
∴曲线C的方程为 +y2=1.
+y2=1.
(2)设直线l的方程为y=kx+2,
代入 +y2=1,得(1+5k2)x2+20kx+15=0.
+y2=1,得(1+5k2)x2+20kx+15=0.
Δ=(20k)2-4×15(1+5k2)>0,得k2> .由图可知
.由图可知 =λ
=λ

由韦达定理得
将x1=λx2代入得
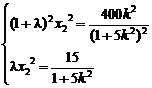
两式相除得

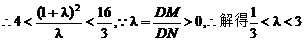 ①
①
 M在D、N中间,∴λ<1 ②
M在D、N中间,∴λ<1 ②
又∵当k不存在时,显然λ=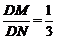 (此时直线l与y轴重合).
(此时直线l与y轴重合).