-
1.()若不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,则a的取值范围是( )
A.(-∞,2
 B.
B. -2,2
-2,2 C.(-2,2
C.(-2,2 D.(-∞,-2)
D.(-∞,-2) -
2.()设二次函数f(x)=x2-x+a(a>0),若f(m)<0,则f(m-1)的值为( )
A.正数 B.负数
C.非负数 D.正数、负数和零都有可能
-
3.()已知二次函数f(x)=4x2-2(p-2)x-2p2-p+1,若在区间[-1,1]内至少存在一个实数c,使f(c)>0,则实数p的取值范围是_________.
-
4.()二次函数f(x)的二次项系数为正,且对任意实数x恒有f(2+x)=f(2-x),若f(1-2x2)<f(1+2x-x2),则x的取值范围是_________.
-
5.()已知实数t满足关系式
 (a>0且a≠1)
(a>0且a≠1)(1)令t=ax,求y=f(x)的表达式;
(2)若x∈(0,2
 时,y有最小值8,求a和x的值.
时,y有最小值8,求a和x的值. -
6.()如果二次函数y=mx2+(m-3)x+1的图象与x轴的交点至少有一个在原点的右侧,试求m的取值范围.
-
7.()二次函数f(x)=px2+qx+r中实数p、q、r满足
 =0,其中m>0,求证:
=0,其中m>0,求证:(1)pf(
 )<0;
)<0;(2)方程f(x)=0在(0,1)内恒有解.
-
8.()一个小服装厂生产某种风衣,月销售量x(件)与售价P(元/件)之间的关系为P=160-2x,生产x件的成本R=500+30x元.
(1)该厂的月产量多大时,月获得的利润不少于1300元?
(2)当月产量为多少时,可获得最大利润?最大利润是多少元?
08高考数学三个“二次”及关系试题 三个“二次”即一元二次函数、一元二次方程、一元二次不等式是中学数学的重要内容,具有丰富的内涵和密切的联系,同时也是研究包含二次曲线在内的许多内容的工具.高考试题中近一半的试题与这三个“二次”问题有关.本节主要是帮助考生理解三者之间的区别及联系,掌握函数、方程及不等式的思想和方法. ●难点磁场 已知对于x的所有实数值,二次函数f(x)=x2-4ax+2a+12(a∈R)的值都是非负的,求关于x的方程=|a-1|+2的根的取值范围. ●案例探究 [例1]已知二次函参考答案
参考答案
难点磁场
解:由条件知Δ≤0,即(-4a)2-4(2a+12)≤0,∴-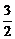 ≤a≤2
≤a≤2
(1)当-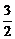 ≤a<1时,原方程化为:x=-a2+a+6,∵-a2+a+6=-(a-
≤a<1时,原方程化为:x=-a2+a+6,∵-a2+a+6=-(a-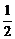 )2+
)2+ .
.
∴a=-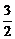 时,xmin=
时,xmin= ,a=
,a=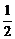 时,xmax=
时,xmax= .
.
∴ ≤x≤
≤x≤ .
.
(2)当1≤a≤2时,x=a2+3a+2=(a+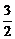 )2-
)2-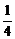
∴当a=1时,xmin=6,当a=2时,xmax=12,∴6≤x≤12.
综上所述, ≤x≤12.
≤x≤12.
歼灭难点训练
一、1.解析:当a-2=0即a=2时,不等式为-4<0,恒成立.∴a=2,当a-2≠0时,则a满足 ,解得-2<a<2,所以a的范围是-2<a≤2.
,解得-2<a<2,所以a的范围是-2<a≤2.
答案:C
2.解析:∵f(x)=x2-x+a的对称轴为x=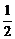 ,且f(1)>0,则f(0)>0,而f(m)<0,∴m∈(0,1),
,且f(1)>0,则f(0)>0,而f(m)<0,∴m∈(0,1),
∴m-1<0,∴f(m-1)>0.
答案:A
二、3.解析:只需f(1)=-2p2-3p+9>0或f(-1)=-2p2+p+1>0即-3<p<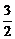 或-
或-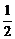 <p<1.∴p∈(-3,
<p<1.∴p∈(-3, 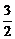 ).
).
答案:(-3,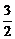 )
)
4.解析:由f(2+x)=f(2-x)知x=2为对称轴,由于距对称轴较近的点的纵坐标较小,
∴|1-2x2-2|<|1+2x-x2-2|,∴-2<x<0.
答案:-2<x<0
三、5.解:(1)由loga 得logat-3=logty-3logta
得logat-3=logty-3logta
由t=ax知x=logat,代入上式得x-3= ,
,
∴logay=x2-3x+3,即y=a (x≠0).
(x≠0).
(2)令u=x2-3x+3=(x-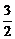 )2+
)2+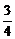 (x≠0),则y=au
(x≠0),则y=au
①若0<a<1,要使y=au有最小值8,
则u=(x-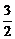 )2+
)2+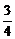 在(0,2
在(0,2 上应有最大值,但u在(0,2
上应有最大值,但u在(0,2 上不存在最大值.
上不存在最大值.
②若a>1,要使y=au有最小值8,则u=(x-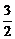 )2+
)2+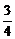 ,x∈(0,2
,x∈(0,2 应有最小值
应有最小值
∴当x=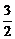 时,umin=
时,umin=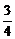 ,ymin=
,ymin=
由 =8得a=16.∴所求a=16,x=
=8得a=16.∴所求a=16,x=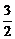 .
.
6.解:∵f(0)=1>0
(1)当m<0时,二次函数图象与x轴有两个交点且分别在y轴两侧,符合题意.
(2)当m>0时,则 解得0<m≤1
解得0<m≤1
综上所述,m的取值范围是{m|m≤1且m≠0}.
7.证明:(1)

 ,由于f(x)是二次函数,故p≠0,又m>0,所以,pf(
,由于f(x)是二次函数,故p≠0,又m>0,所以,pf( )<0.
)<0.
(2)由题意,得f(0)=r,f(1)=p+q+r
①当p<0时,由(1)知f( )<0
)<0
若r>0,则f(0)>0,又f( )<0,所以f(x)=0在(0,
)<0,所以f(x)=0在(0, )内有解;
)内有解;
若r≤0,则f(1)=p+q+r=p+(m+1)=(- )+r=
)+r= >0,
>0,
又f( )<0,所以f(x)=0在(
)<0,所以f(x)=0在( ,1)内有解.
,1)内有解.
②当p<0时同理可证.
8.解:(1)设该厂的月获利为y,依题意得
y=(160-2x)x-(500+30x)=-2x2+130x-500
由y≥1300知-2x2+130x-500≥1300
∴x2-65x+900≤0,∴(x-20)(x-45)≤0,解得20≤x≤45
∴当月产量在20~45件之间时,月获利不少于1300元.
(2)由(1)知y=-2x2+130x-500=-2(x-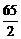 )2+1612.5
)2+1612.5
∵x为正整数,∴x=32或33时,y取得最大值为1612元,
∴当月产量为32件或33件时,可获得最大利润1612元.