-
1.()已知方程x2+4ax+3a+1=0(a>1)的两根均tanα、tanβ,且α,β∈
(-
 ),则tan
),则tan 的值是( )
的值是( )A.
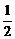 B.-2
C.
B.-2
C. D.
D.
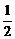 或-2
或-2 -
2.()已知sinα=
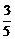 ,α∈(
,α∈(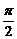 ,π),tan(π-β)=
,π),tan(π-β)= 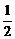 ,则tan(α-2β)=_________.
,则tan(α-2β)=_________. -
3.()设α∈(
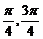 ),β∈(0,
),β∈(0, ),cos(α-
),cos(α- )=
)=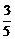 ,sin(
,sin( +β)=
+β)= ,则sin(α+β)=_________.
,则sin(α+β)=_________. -
4.不查表求值:

-
5.已知cos(
 +x)=
+x)=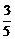 ,(
,(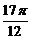 <x<
<x< ),求
),求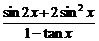 的值.
的值. -
6.()已知α-β=
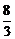 π,且α≠kπ(k∈Z).求
π,且α≠kπ(k∈Z).求 的最大值及最大值时的条件.
的最大值及最大值时的条件. -
7.
 ()如右图,扇形OAB的半径为1,中心角60°,四边形PQRS是扇形的内接矩形,当其面积最大时,求点P的位置,并求此最大面积.
()如右图,扇形OAB的半径为1,中心角60°,四边形PQRS是扇形的内接矩形,当其面积最大时,求点P的位置,并求此最大面积. -
8.()已知cosα+sinβ=
 ,sinα+cosβ的取值范围是D,x∈D,求函数y=
,sinα+cosβ的取值范围是D,x∈D,求函数y= 的最小值,并求取得最小值时x
的最小值,并求取得最小值时x
难点16 三角函数式的化简与求值 三角函数式的化简和求值是高考考查的重点内容之一.通过本节的学习使考生掌握化简和求值问题的解题规律和途径,特别是要掌握化简和求值的一些常规技巧,以优化我们的解题效果,做到事半功倍. ●难点磁场 ()已知<β<α<,cos(α-β)=,sin(α+β)=-,求sin2α的值_________. ●案例探究 [例1]不查表求sin220°+cos280°+cos20°cos80°的值. 命题意图:本题主要考查两角和、二倍角公式及降幂求值的方法,对计算能力的要求较高参考答案
的值.
参考答案
难点磁场
解法一:∵ <β<α<
<β<α<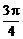 ,∴0<α-β<
,∴0<α-β<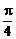 .π<α+β<
.π<α+β<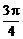 ,
,
∴sin(α-β)=
∴sin2α=sin[(α-β)+(α+β)]
=sin(α-β)cos(α+β)+cos(α-β)sin(α+β)
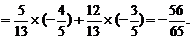
解法二:∵sin(α-β)= ,cos(α+β)=-
,cos(α+β)=- ,
,
∴sin2α+sin2β=2sin(α+β)cos(α-β)=-
sin2α-sin2β=2cos(α+β)sin(α-β)=-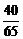
∴sin2α=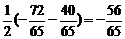
歼灭难点训练
一、1.解析:∵a>1,tanα+tanβ=-4a<0.
tanα+tanβ=3a+1>0,又α、β∈(- ,
, )∴α、β∈(-
)∴α、β∈(- ,θ),则
,θ),则 ∈(-
∈(- ,0),又tan(α+β)=
,0),又tan(α+β)= ,
,
整理得2tan2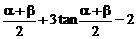 =0.解得tan
=0.解得tan =-2.
=-2.
答案:B
2.解析:∵sinα=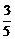 ,α∈(
,α∈( ,π),∴cosα=-
,π),∴cosα=-
则tanα=- ,又tan(π-β)=
,又tan(π-β)=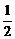 可得tanβ=-
可得tanβ=-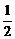 ,
,

答案: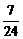
3.解析:α∈( ),α-
),α-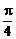 ∈(0,
∈(0,  ),又cos(α-
),又cos(α-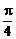 )=
)=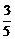 .
.
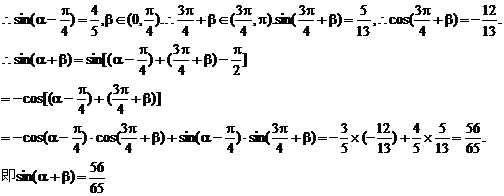
答案: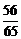
三、4.答案:2
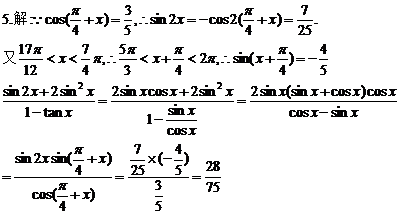
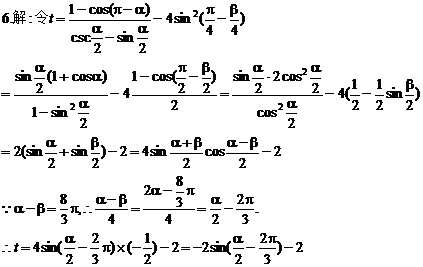
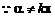 (k∈Z),
(k∈Z), (k∈Z)
(k∈Z)
∴当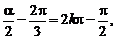 即
即 (k∈Z)时,
(k∈Z)时,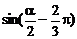 的最小值为-1.
的最小值为-1.
7.解:以OA为x轴.O为原点,建立平面直角坐标系,并设P的坐标为(cosθ,sinθ),则
|PS|=sinθ.直线OB的方程为y= x,直线PQ的方程为y=sinθ.联立解之得Q(
x,直线PQ的方程为y=sinθ.联立解之得Q( sinθ;sinθ),所以|PQ|=cosθ-
sinθ;sinθ),所以|PQ|=cosθ- sinθ.
sinθ.
于是SPQRS=sinθ(cosθ- sinθ)=
sinθ)= (
( sinθcosθ-sin2θ)=
sinθcosθ-sin2θ)= (
(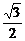 sin2θ-
sin2θ- )=
)= (
(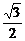 sin2θ+
sin2θ+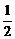 cos2θ-
cos2θ-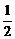 )=
)=  sin(2θ+
sin(2θ+ )-
)- .
.
∵0<θ< ,∴
,∴ <2θ+
<2θ+ <
< π.∴
π.∴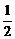 <sin(2θ+
<sin(2θ+ )≤1.
)≤1.
∴sin(2θ+ )=1时,PQRS面积最大,且最大面积是
)=1时,PQRS面积最大,且最大面积是 ,此时,θ=
,此时,θ= ,点P为
,点P为 的中点,P(
的中点,P( ).
).
8.解:设u=sinα+cosβ.则u2+( )2=(sinα+cosβ)2+(cosα+sinβ)2=2+2sin(α+β)≤4.∴u2≤1,-1≤u≤1.即D=[-1,1],设t=
)2=(sinα+cosβ)2+(cosα+sinβ)2=2+2sin(α+β)≤4.∴u2≤1,-1≤u≤1.即D=[-1,1],设t= ,∵-1≤x≤1,∴1≤t≤
,∵-1≤x≤1,∴1≤t≤ .x=
.x= .
.
