-
1、已知:
 (其中
(其中 、
、 为实数,
为实数,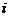 为虚数单位)。则
为虚数单位)。则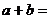 ;
; -
2、若
 ,
, ,则
,则 ;
; -
3、已知:
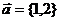 ,
, ,且
,且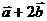 与
与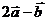 平行,则
平行,则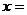 ;
; -
4、已知
 ,
, 的最小值为
;
的最小值为
; -
5、在一个袋子里有10个红球和2个白球,现从中随机拿出3个,则其中至少有一个白球的概率是
(用分数表示);
-
6、参数方程
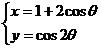 (
(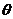 为参数方程)所表示的曲线的焦点的直角坐标是
;
为参数方程)所表示的曲线的焦点的直角坐标是
; -
7、经过点A
 ,(
,( ),且与极轴正方向夹角为
),且与极轴正方向夹角为 的直线的极坐标方程为
;
的直线的极坐标方程为
; -
8、若直线
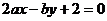 (
( ),始终平分圆
),始终平分圆 的周长,则
的周长,则 的最大值为
;
的最大值为
; -
9、已知:函数
 (
( )在区间
)在区间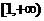 上单调递减,则实数
上单调递减,则实数 取值范围是 ;
取值范围是 ; -
10、数列
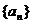 是等差数列,前
是等差数列,前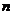 项和为
项和为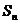 ,
, ,
,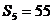 ,则过点
,则过点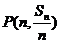 ,
,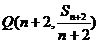 的直线斜率为
;
的直线斜率为
; -
11、设集合
 ,若
,若 ,则把
,则把 的所有元素的乘积称为
的所有元素的乘积称为 的容量(若
的容量(若 中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为0)。若
中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为0)。若 的容量为奇(偶)数,则称为奇(偶)子集。若
的容量为奇(偶)数,则称为奇(偶)子集。若 ,则
,则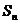 的所有奇子集的容量之和为 ;
的所有奇子集的容量之和为 ; -
12、
 的必要非充分条件是……………………………………………………………( )
的必要非充分条件是……………………………………………………………( )A、
 B、
B、 C、
C、 D、
D、
-
13、已知:
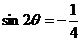 ,且
,且 ,则
,则 ……………………………( )
……………………………( )A、
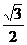 B、
B、 C、
C、 D、
D、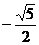
-
14、直线
 在平面
在平面 内,则“平面
内,则“平面 ∥平面
∥平面 ”是“直线
”是“直线 ∥在平面
∥在平面 ”的…………( )
”的…………( )A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分也非必要条件
-
15、函数
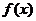 的反函数图像向左平移一个单位得到曲线
的反函数图像向左平移一个单位得到曲线 ,函数
,函数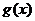 的图像与曲线
的图像与曲线 关于
关于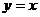 成轴对称,则
成轴对称,则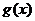 等于…………………………………………………………( )
等于…………………………………………………………( )A、
 B、
B、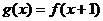 C、
C、 D、
D、
-
16、(本题满分12分,第1小题8分,第2小题4分)
若复数
 (
( ),且
),且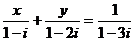 ,
,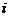 是虚数单位
是虚数单位(1)求复数
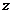 ;
;(2)求
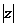 。、
。、 -
17、(本题满分14分,第1小题6分,第2小题8分)
已知:正方体
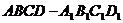 的棱长为2,点
的棱长为2,点 分别在底面正方形的边
分别在底面正方形的边 、
、 上,且
上,且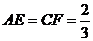 ,点
,点 是棱
是棱 的中点。
的中点。(1)在图中画出经过三点正方体
 的截面,并保留作图痕迹;
的截面,并保留作图痕迹;(2)求(1)中的截面与底面
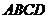 所成锐二面角的大小;
所成锐二面角的大小;
-
18、(本题满分14分,第1小题4分,第2小题10分)
数列
 的前
的前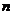 项和
项和 (
(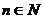 )
)(1)求数列
 的通项;
的通项;(2)数列
 满足
满足 ,
,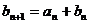 (
(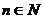 ),求
),求 的通项及前
的通项及前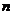 项和
项和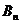 ;
; -
19、(本题满分16分,第1小题8分,第2小题8分)
已知:某型号进口仪器每台降价
 成(1成为
成(1成为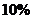 ),那么售出数量就增加
),那么售出数量就增加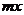 成(
成(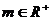 常数)
常数)(1)当某商场现在定价为每台
 元,售出
元,售出 台,试建立降价后的营业额
台,试建立降价后的营业额 与每台降价
与每台降价 成的函数关系式,并求出
成的函数关系式,并求出 时,每台降价多少成时,营业额
时,每台降价多少成时,营业额 最大?
最大?(2)为使营业额增加,求
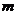 的取值范围。
的取值范围。 -
20、(本题满分16分,第1小题8分,第2小题8分)
设
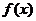 是定义在
是定义在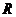 上的偶函数,图像关于直线
上的偶函数,图像关于直线 对称,且对
对称,且对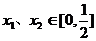 ,有
,有
(1)设
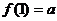 ,探求
,探求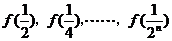 的值;
的值;(2)求证:
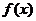 是以2为周期的函数,并将该命题加以推广。
是以2为周期的函数,并将该命题加以推广。 -
21、(本题满分18分,第1小题4分,第2小题8分,第3小题6分)
已知:一椭圆两焦点坐标分别为
 、
、 ,且椭圆上一点
,且椭圆上一点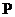 到两焦点的距离和为4
到两焦点的距离和为4(1)求该椭圆的方程;
(2)设点
 在椭圆上,且
在椭圆上,且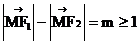 ,试把
,试把 表示为
表示为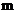 的函数
的函数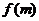 ;
;(3)试证:方程
 至多只有一个实数根。
至多只有一个实数根。
08届高考理科数学联考试卷参考答案
参考答案
一、填空题(本大题满分44分,共11题,每题4分,只要求直接填写结果)
1、已知: (其中
(其中 、
、 为实数,
为实数,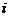 为虚数单位)。则
为虚数单位)。则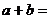 2 ;
2 ;
2、若 ,
, ,则
,则 12 ;
12 ;
3、已知: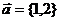 ,
, ,且
,且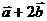 与
与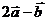 平行,则
平行,则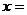
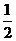 ;
;
4、已知 ,
, 的最小值为
的最小值为  ;
;
5、在一个袋子里有10个红球和2个白球,现从中随机拿出3个,则其中至少有一个白球的概率是
 (用分数表示);
(用分数表示);
6、参数方程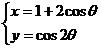 (
(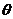 为参数方程)所表示的曲线的焦点的直角坐标是
为参数方程)所表示的曲线的焦点的直角坐标是  ;
;
7、经过点A ,(
,( ),且与极轴正方向夹角为
),且与极轴正方向夹角为 的直线的极坐标方程为
的直线的极坐标方程为
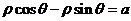 ;
;
8、若直线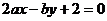 (
( ),始终平分圆
),始终平分圆 的周长,则
的周长,则 的最大值为
的最大值为  ;
;
9、已知:函数 (
( )在区间
)在区间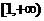 上单调递减,则实数
上单调递减,则实数 取值范围是
取值范围是  ;
;
10、数列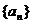 是等差数列,前
是等差数列,前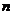 项和为
项和为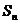 ,
, ,
,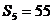 ,则过点
,则过点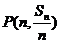 ,
,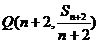 的直线斜率为
2 ;
的直线斜率为
2 ;
11、设集合 ,若
,若 ,则把
,则把 的所有元素的乘积称为
的所有元素的乘积称为 的容量(若
的容量(若 中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为0)。若
中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为0)。若 的容量为奇(偶)数,则称为奇(偶)子集。若
的容量为奇(偶)数,则称为奇(偶)子集。若 ,则
,则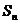 的所有奇子集的容量之和为 7
;
的所有奇子集的容量之和为 7
;
二、选择题(本大题满分16分,共4题,每题有且仅有一个正确答案)
12、 的必要非充分条件是……………………………………………(A )
的必要非充分条件是……………………………………………(A )
A、 B、
B、 C、
C、 D、
D、
13、已知: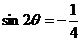 ,且
,且 ,则
,则 ……………………………( D )
……………………………( D )
A、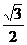 B、
B、 C、
C、 D、
D、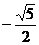
14、直线 在平面
在平面 内,则“平面
内,则“平面 ∥平面
∥平面 ”是“直线
”是“直线 ∥在平面
∥在平面 ”的…………( A )
”的…………( A )
A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分也非必要条件
15、函数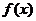 的反函数图像向左平移一个单位得到曲线
的反函数图像向左平移一个单位得到曲线 ,函数
,函数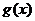 的图像与曲线
的图像与曲线 关于
关于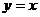 成轴对称,则
成轴对称,则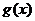 等于…………………………………………………………(A )
等于…………………………………………………………(A )
A、 B、
B、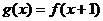 C、
C、 D、
D、
三、解答题
16、(本题满分12分,第1小题8分,第2小题4分)
若复数 (
( ),且
),且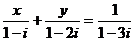 ,
,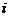 是虚数单位
是虚数单位
(1)求复数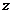 ;
;
(2)求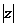 。、
。、
(1)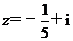 (2)
(2) 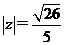 。
。
17、(本题满分14分,第1小题6分,第2小题8分)
已知:正方体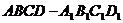 的棱长为2,点
的棱长为2,点 分别在底面正方形的边
分别在底面正方形的边 、
、 上,且
上,且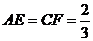 ,点
,点 是棱
是棱 的中点。
的中点。
(1)在图中画出经过三点正方体 的截面,并保留作图痕迹;
的截面,并保留作图痕迹;
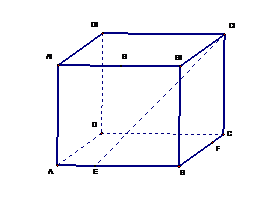 (2)求(1)中的截面与底面
(2)求(1)中的截面与底面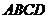 所成锐二面角的大小;
所成锐二面角的大小;

18、(本题满分14分,第1小题4分,第2小题10分)
数列 的前
的前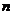 项和
项和 (
(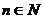 )
)
(1)求数列 的通项;
的通项;

(2)数列 满足
满足 ,
,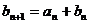 (
(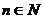 ),求
),求 的通项及前
的通项及前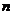 项和
项和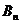 ;
;

19、(本题满分16分,第1小题8分,第2小题8分)
已知:某型号进口仪器每台降价 成(1成为
成(1成为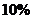 ),那么售出数量就增加
),那么售出数量就增加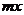 成(
成(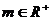 常数)
常数)
(1)当某商场现在定价为每台 元,售出
元,售出 台,试建立降价后的营业额
台,试建立降价后的营业额 与每台降价
与每台降价 成的函数关系式,并求出
成的函数关系式,并求出 时,每台降价多少成时,营业额
时,每台降价多少成时,营业额 最大?
最大?
解:
当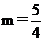 时,x=1,营业额最大,降价1成时。
时,x=1,营业额最大,降价1成时。
(2)为使营业额增加,求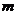 的取值范围。
的取值范围。
解:为使营业额增加,

20、(本题满分16分,第1小题8分,第2小题8分)
设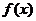 是定义在
是定义在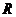 上的偶函数,图像关于直线
上的偶函数,图像关于直线 对称,且对
对称,且对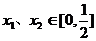 ,有
,有
(1)设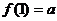 ,探求
,探求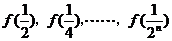 的值;
的值;
(2)求证: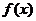 是以2为周期的函数,并将该命题加以推广。
是以2为周期的函数,并将该命题加以推广。
21、(本题满分18分,第1小题4分,第2小题8分,第3小题6分)
已知:一椭圆两焦点坐标分别为 、
、 ,且椭圆上一点
,且椭圆上一点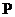 到两焦点的距离和为4
到两焦点的距离和为4
(1)求该椭圆的方程;
(2)设点 在椭圆上,且
在椭圆上,且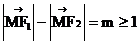 ,试把
,试把 表示为
表示为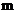 的函数
的函数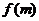 ;
;
(3)试证:方程 至多只有一个实数根。
至多只有一个实数根。
解:(1)该椭圆的方程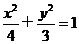 ;
;
(2)
(3)(反证法)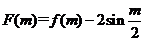
如果至少存在两个不相等的实数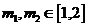 ,不妨设
,不妨设 上为减函数,
上为减函数,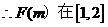 上为减函数。
上为减函数。
故 ,这与
,这与 相矛盾。因此,满足方程
相矛盾。因此,满足方程 至多只有一个实数根。
至多只有一个实数根。