-
13.某校有老师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量为n的样本;已知从女学生中抽取的人数为80人,则n= .
-
14.F1,F2是椭圆C:
 的焦点,在C上满足PF1⊥PF2的点P的个数为__________.
的焦点,在C上满足PF1⊥PF2的点P的个数为__________. -
15、如果过两点
 和
和 的直线与抛物线
的直线与抛物线 没有交点,那么实数
没有交点,那么实数 的取值范围是__________________.
的取值范围是__________________. -
16.有以下四个命题:
(A)曲线
 按
按 平移可得曲线
平移可得曲线 ;
;(B)设
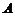 、
、 为两个定点,
为两个定点, 为常数,
为常数,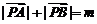 ,则动点
,则动点 的轨迹为椭圆;
的轨迹为椭圆;(C)若|x|+|y|
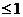 ,则使
,则使 取得最大值和最小值的最优解都有无数多个;
取得最大值和最小值的最优解都有无数多个;(D)若椭圆的左、右焦点分别为
 、
、 ,
, 是该椭圆上的任意一点,则点
是该椭圆上的任意一点,则点 关于“
关于“ 的外角平分线”的对称点
的外角平分线”的对称点 的轨迹是圆
的轨迹是圆
其中真命题的序号为
 .(写出所有真命题的代号)
.(写出所有真命题的代号) -
17.(本小题满分12分)
已知α为第二象限角,且 sinα=
 求
求 的值
的值 -
18.已知直线
 为曲线
为曲线 在点(1,0)处的切线,
在点(1,0)处的切线, 为该曲线的另一条切线,且
为该曲线的另一条切线,且
(Ⅰ)求直线
 的方程;
的方程;(Ⅱ)求由直线
 、
、 和
和 轴所围成的三角形的面积
轴所围成的三角形的面积 -
19.已知
 的反函数为
的反函数为 ,
, .
.(1)若
 ,求
,求 的取值范围D;
的取值范围D;(2)设函数
 ,当
,当 时,求函数
时,求函数 的值域.
的值域. -
20.
 如图,圆
如图,圆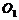 与圆
与圆 的半径都是1,
的半径都是1, . 过动点
. 过动点 分别作圆
分别作圆 、圆
、圆 的切线
的切线 (
( 分别为切点),使得
分别为切点),使得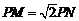 . 试建立适当的坐标系,并求动点
. 试建立适当的坐标系,并求动点 的轨迹方程。
的轨迹方程。 -
21.(本小题满分12分)
在数列
 中,
中, ,
, ,
, .
.(Ⅰ)证明数列
 是等比数列;
是等比数列;(Ⅱ)求数列
 的前
的前 项和
项和 ;
;(Ⅲ)证明不等式
 ,对任意
,对任意 皆成立.
皆成立. -
22.(本小题满分14分)
椭圆的中心是原点O,它的短轴长为
 ,相应于焦点
,相应于焦点 的准线
的准线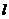 与
与 轴相交于点A,
轴相交于点A, ,过点A的直线与椭圆相交于P、Q两点.
,过点A的直线与椭圆相交于P、Q两点.(I) 求椭圆的方程及离心率;
(II)若
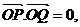 求直线PQ的方程.
求直线PQ的方程.
08届高考数学江西省第五次月考试卷 文科 命题人:张景智 一选择题 1.若U={1,2,3,4}, M={1,2},N={2,3}, 则( ) (A) {1,2,3} (B) {2} (C) {1,3,4} (D) {4} 2. 点P从(1,0)出发,沿单位圆逆时针方向运动弧长到达Q点, 则Q的坐标为( ) (A) (B) ( (C) ( (D)参考答案
参考答案
文科
一选择题
1、D 2、A 3、B 4、C 5、C 6、B 7、A 8、A 9、D 10、C 11、A 12、D
二.填空题
13. 192 14。 2 15。  16. C、D
16. C、D
三、解答题
17.解:

当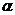 为第二象限角,且
为第二象限角,且 时
时  ,
,
所以 =
=
18. 解:(Ⅰ)y′=2x+1.
直线l1的方程为y=3x-3.
设直线l2过曲线y=x2+x-2上 的点B(b, b2+b-2),则l2的方程为y=(2b+1)x-b2-2
因为l1⊥l2,则有2b+1=
所以直线l2的方程为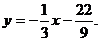
(II)解方程组 得
得
所以直线l1和l2的交点的坐标为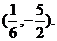
l1、l2与x轴交点的坐标分别为(1,0)、 .
.
所以所求三角形的面积
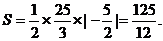
19.解:(1)∵ ,∴
,∴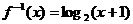 (x>-1)
(x>-1)
由 ≤g(x) ∴
≤g(x) ∴ ,解得0≤x≤1 ∴D=[0,1]
,解得0≤x≤1 ∴D=[0,1]
(2)H(x)=g(x)-
∵0≤x≤1 ∴1≤3-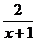 ≤2
≤2
∴0≤H(x)≤ ∴H(x)的值域为[0,
∴H(x)的值域为[0, ]
]
20.解:以 的中点
的中点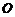 为原点,
为原点, 所在直线为
所在直线为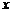 轴,建立如图所示的平面直角坐标系,则
轴,建立如图所示的平面直角坐标系,则 ,
, 。
。
由已知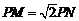 ,得
,得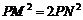 。
。
因为两圆半径均为1,所以 。
。
设 ,则
,则 ,
,
即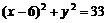 (或
(或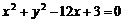 )。
)。
21.(Ⅰ)证明:由题设 ,得
,得
 ,
, .
.
又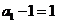 ,所以数列
,所以数列 是首项为
是首项为 ,且公比为
,且公比为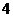 的等比数列.
的等比数列.
(Ⅱ)解:由(Ⅰ)可知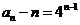 ,于是数列
,于是数列 的通项公式为
的通项公式为
 .
.
所以数列 的前
的前 项和
项和 .
.
(Ⅲ)证明:对任意的 ,
,
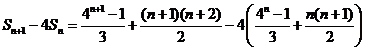
 .
.
所以不等式 ,对任意
,对任意 皆成立.
皆成立.
22.(I)解:由题意,可设椭圆的方程为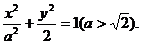
由已知得

解得 
所以椭圆的方程为 ,离心率
,离心率 ………………4分
………………4分
(II)解: 由(I)可得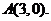
设直线PQ的方程为 由方程组
由方程组
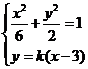
得 
依题意  得
得

设  则
则
 ①
①
 ②
②
由直线PQ的方程得 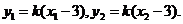 于是
于是
 ③
③
 ④
④
由①②③④得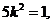 从而
从而
所以直线PQ的方程为
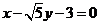 或
或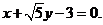 ……………………14分
……………………14分