-
1. 设集合
 等于
等于A.
 B.
B. C.
C. D.
D.
-
2.
 等于
等于A.
 B.
B. C.
C. D.
D.
-
3. 下列函数中,最小正周期为
 ,且图象关于直线
,且图象关于直线 对称的是
对称的是A.
 B.
B. C.
C. D.
D.
-
4. 下列所给4个图象中,与所给3件事吻合顺序最好的为
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
 (3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。A、(1)(2)(4) B、(4)(2)(3) C、(4)(1)(2) D、(4)(1)(3)
-
5. 在等比数列
 中,已知
中,已知 是关于
是关于 方程
方程 的两个根,则
的两个根,则 等于
等于(A)
 (B)25
(C)
(B)25
(C)  (D)
(D)

-
6.
 右边程序运行的结果是
右边程序运行的结果是A.1,2,3 B. 3,2,1 C. 2,3,1 D2,3,2
-
7. 已知函数f(x)=x3+ax2,点P(-1,b)在曲线y=f(x) 上,
则以P为切点且平行于直线3x+y=0的切线方程为
A.3x+y-1=0 B.3x+y-2=0
C.3x-y+1=0 D.3x+y+1=0
-
8. 定义运算
 =ad-bc,则符合条件
=ad-bc,则符合条件 =0
=0的点P(x,y)的轨迹方程为
A. (x-1)2+4y2=1 B.(x-1)2-4y2=1 C.(x-1)2+y2=1 D.(x-1)2-y2=1
-
9. 下图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第n个图案中需用黑色瓷砖___________块.(用含n的代数式表示)

-
10.若向量
 满足
满足 与
与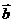 的夹角为120°,则
的夹角为120°,则 .
. -
11.
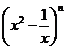 的展开式中,常数项为
的展开式中,常数项为 ,则
,则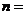 _____
____________.
_____
____________. -
12. 等体积的球和正方体,它们的表面积的大小关系是
 _____
_____ .
.(填”大于、小于或等于”).
-
13.(坐标系与参数方程选做题).已知点
 在曲线
在曲线
 (
( 为参数)上,则
为参数)上,则 的取值范围为
.
的取值范围为
. -
14.(不等式选讲选做题)设函数
 =
;若
=
;若 ,则
,则 的取值范围是
.
的取值范围是
. -
15.
 (几何证明选讲选做题)如图, AC为⊙O的直径,BD⊥AC于P,PC=2,PA=8
(几何证明选讲选做题)如图, AC为⊙O的直径,BD⊥AC于P,PC=2,PA=8则CD的长为 、cos∠ACB= .(用数字表示)
-
16.(本小题满分12分)
在△ABC中,a=
 ,b=2,c=
,b=2,c= +1,求A、B、C及S△ABC.
+1,求A、B、C及S△ABC. -
17.(本题满分12分)
已知数列
 的前n项和
的前n项和
(Ⅰ)求通项
 ;
;(Ⅱ)求和:

-
18.(本小题满分14分)
已知某椭圆的焦点是
 、
、 ,过点F2并垂直于x轴的直线与椭圆的一个交点为B,且
,过点F2并垂直于x轴的直线与椭圆的一个交点为B,且 ,椭圆上不同的两点
,椭圆上不同的两点 、
、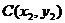 满足条件:
满足条件: 、
、 、
、 成等差数列.
成等差数列.(I)求该椭圆的方程;
(II)求弦AC中点的横坐标.

-
19.(本小题满分14分)
在直三棱柱ABC-A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BA、BC的中点,G是AA1上一点,且AC1⊥EG.
 (Ⅰ)确定点G的位置;
(Ⅰ)确定点G的位置;(Ⅱ)求直线AC1与平面EFG所成角θ的大小.
-
20.(本小题满分14分)
甲、乙、丙三个口袋内都分别装有6个不相同的球,并且每个口袋内的6个球均有1个红球,2个黑球,3个无色透明的球,现从甲、乙、丙三个口袋中依次随机各摸出1个球.
(1)求恰好摸出红球、黑球和无色球各1个的概率;
(2)求摸出的3个球中含有有色球数ξ的概率分布列和数学期望.
-
21.(本小题满分14分)
已知函数
 的图像过点
的图像过点 ,且
,且 对任意实数都成立,函数
对任意实数都成立,函数 与
与 的图像关于原点对称。
的图像关于原点对称。⑴ 求
 与
与 的解析式;
的解析式;⑵ 若
 在[-1,1]上是增函数,求实数λ的取值范围;
在[-1,1]上是增函数,求实数λ的取值范围;