-
21.解:(1)由

整理得
 .
.又
 ,所以
,所以 是首项为
是首项为 ,公比为
,公比为 的等比数列,得
的等比数列,得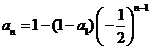
(2)方法一:
由(1)可知
 ,故
,故 .
.那么,


又由(1)知
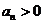 且
且 ,故
,故 ,
,因此
 为正整数.
为正整数.方法二:
由(1)可知
 ,
,因为
 ,
,所以
 .
.由
 可得
可得 ,
,即

两边开平方得
 .
.即
 为正整数.
为正整数.全国2文17
设等比数列
 的公比
的公比 ,前
,前 项和为
项和为 .已知
.已知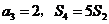 ,求
,求 的通项公式.
的通项公式.解:由题设知
 ,
,则
 ②
②由②得
 ,
, ,
, ,
,因为
 ,解得
,解得 或
或 .
.当
 时,代入①得
时,代入①得 ,通项公式
,通项公式 ;
;当
 时,代入①得
时,代入①得 ,通项公式
,通项公式 .
.全国1理22
已知数列
 中
中 ,
, ,
, .
.(Ⅰ)求
 的通项公式;
的通项公式;(Ⅱ)若数列
 中
中 ,
, ,
, ,
,证明:
 ,
, .
.解:(Ⅰ)由题设:

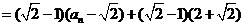
 ,
, .
.所以,数列
 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,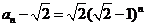 ,
,即
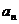 的通项公式为
的通项公式为 ,
, .
.(Ⅱ)用数学归纳法证明.
(ⅰ)当
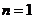 时,因
时,因 ,
, ,所以
,所以 ,结论成立.
,结论成立.(ⅱ)假设当
 时,结论成立,即
时,结论成立,即 ,
,也即
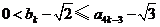 .
.当
 时,
时,
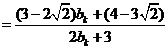
 ,
,又
 ,
,所以

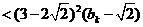

 .
.也就是说,当
 时,结论成立.
时,结论成立.根据(ⅰ)和(ⅱ)知
 ,
, .
.全国1文21
设
 是等差数列,
是等差数列,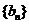 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且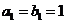 ,
, ,
,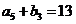
(Ⅰ)求
 ,
,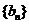 的通项公式;
的通项公式;(Ⅱ)求数列
 的前n项和
的前n项和 .
.解:(Ⅰ)设
 的公差为
的公差为 ,
, 的公比为
的公比为 ,则依题意有
,则依题意有 且
且
解得
 ,
, .
.所以
 ,
, .
.(Ⅱ)
 .
. ,①
,① ,②
,②②-①得
 ,
,

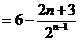 .
.辽宁理21
已知数列
 ,
,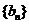 与函数
与函数 ,
, ,
, 满足条件:
满足条件: ,
,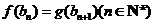 .
.(I)若
 ,
,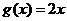 ,
, ,
, 存在,求
存在,求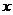 的取值范围;
的取值范围;(II)若函数
 为
为 上的增函数,
上的增函数, ,
, ,
,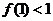 ,证明对任意
,证明对任意 ,
, (用
(用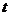 表示).
表示).江西理22
设正整数数列
 满足:
满足: ,且对于任何
,且对于任何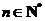 ,有
,有 .
.(1)求
 ,
,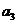 ;
;(3)求数列
 的通项
的通项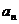 .
.解:(1)据条件得
 ①
①当
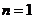 时,由
时,由 ,即有
,即有 ,
,解得
 .因为
.因为 为正整数,故
为正整数,故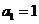 .
.当
 时,由
时,由 ,
,解得
 ,所以
,所以 .
.(2)方法一:由
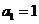 ,
, ,
, ,猜想:
,猜想: .
.下面用数学归纳法证明.
1
 当
当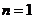 ,
, 时,由(1)知
时,由(1)知 均成立;
均成立;2
 假设
假设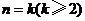 成立,则
成立,则 ,则
,则 时
时由①得
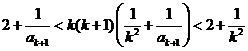


因为
 时,
时, ,所以
,所以 .
. ,所以
,所以 .
.又
 ,所以
,所以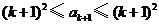 .
.故
 ,即
,即 时,
时, 成立.
成立.由1
 ,2
,2 知,对任意
知,对任意 ,
, .
.(2)方法二:
由
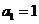 ,
, ,
, ,猜想:
,猜想: .
.下面用数学归纳法证明.
1
 当
当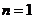 ,
, 时,由(1)知
时,由(1)知 均成立;
均成立;2
 假设
假设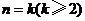 成立,则
成立,则 ,则
,则 时
时由①得
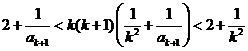
即
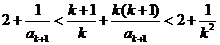 ②
②由②左式,得
 ,即
,即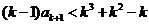 ,因为两端为整数,
,因为两端为整数,则
 .于是
.于是 ③
③又由②右式,
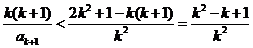 .
.则
 .
.因为两端为正整数,则
 ,
,所以
 .
.又因
 时,
时, 为正整数,则
为正整数,则 ④
④据③④
 ,即
,即 时,
时, 成立.
成立.由1
 ,2
,2 知,对任意
知,对任意 ,
, .
.江西文21
设
 为等比数列,
为等比数列,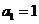 ,
, .
.(1)求最小的自然数
 ,使
,使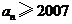 ;
;(2)求和:
 .
.解:(1)由已知条件得
 ,
,因为
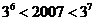 ,所以,使
,所以,使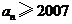 成立的最小自然数
成立的最小自然数 .
.(2)因为
 ,…………①
,…………① ,…………②
,…………② 得:
得:

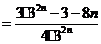
所以
 .
.江苏理20
已知
 是等差数列,
是等差数列,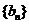 是公比为
是公比为 的等比数列,
的等比数列, ,记
,记 为数列
为数列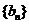 的前
的前 项和,
项和,(1)若
 是大于
是大于 的正整数
的正整数 ,求证:
,求证: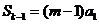 ;(4分)
;(4分)(2)若
 是某一正整数
是某一正整数 ,求证:
,求证: 是整数,且数列
是整数,且数列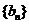 中每一项都是数列
中每一项都是数列 中的项;(8分)
中的项;(8分)(3)是否存在这样的正数
 ,使等比数列
,使等比数列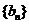 中有三项成等差数列?若存在,写出一个
中有三项成等差数列?若存在,写出一个 的值,并加以说明;若不存在,请说明理由;(4分)
的值,并加以说明;若不存在,请说明理由;(4分)解:设
 的公差为
的公差为 ,由
,由 ,知
,知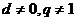 ,
, (
(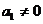 )
)(1)因为
 ,所以
,所以 ,
, ,
,所以

(2)
 ,由
,由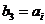 ,
,所以
 解得,
解得, 或
或 ,但
,但 ,所以
,所以 ,因为
,因为 是正整数,所以
是正整数,所以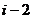 是整数,即
是整数,即 是整数,设数列
是整数,设数列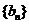 中任意一项为
中任意一项为 ,设数列
,设数列 中的某一项
中的某一项
 =
=
现在只要证明存在正整数
 ,使得
,使得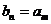 ,即在方程
,即在方程 中
中 有正整数解即可,
有正整数解即可,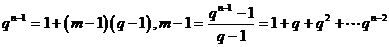 ,所以
,所以 ,若
,若 ,则
,则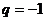 ,那么
,那么 ,当
,当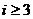 时,因为
时,因为 ,只要考虑
,只要考虑 的情况,因为
的情况,因为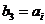 ,所以
,所以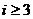 ,因此
,因此 是正整数,所以
是正整数,所以 是正整数,因此数列
是正整数,因此数列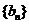 中任意一项为
中任意一项为 与数列
与数列 的第
的第 项相等,从而结论成立。
项相等,从而结论成立。(3)设数列
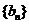 中有三项
中有三项 成等差数列,则有
成等差数列,则有2
 设
设 ,所以2
,所以2 ,令
,令 ,则
,则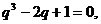
 ,因为
,因为 ,所以
,所以 ,所以
,所以 ,即存在
,即存在 使得
使得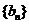 中有三项
中有三项 成等差数列。
成等差数列。湖南理21
已知
 (
( )是曲线
)是曲线 上的点,
上的点,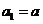 ,
, 是数列
是数列 的前
的前 项和,且满足
项和,且满足 ,
, ,
,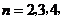 ….
….(I)证明:数列
 (
( )是常数数列;
)是常数数列;(II)确定
 的取值集合
的取值集合 ,使
,使 时,数列
时,数列 是单调递增数列;
是单调递增数列;(III)证明:当
 时,弦
时,弦 (
( )的斜率随
)的斜率随 单调递增
单调递增解:(I)当
 时,由已知得
时,由已知得 .
.因为
 ,所以
,所以 .
…… ①
.
…… ①于是
 .
……②
.
……②由②-①得
 .
…… ③
.
…… ③于是
 .
…… ④
.
…… ④由④-③得
 ,
…… ⑤
,
…… ⑤所以
 ,即数列
,即数列 是常数数列.
是常数数列.(II)由①有
 ,所以
,所以 .由③有
.由③有 ,
, ,所以
,所以 ,
, .
.而 ⑤表明:数列
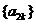 和
和 分别是以
分别是以 ,
,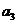 为首项,6为公差的等差数列,
为首项,6为公差的等差数列,所以
 ,
, ,
, ,
,数列
 是单调递增数列
是单调递增数列 且
且 对任意的
对任意的 成立.
成立. 且
且

 .
.即所求
 的取值集合是
的取值集合是 .
.(III)解法一:弦
 的斜率为
的斜率为
任取
 ,设函数
,设函数 ,则
,则
记
 ,则
,则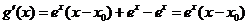 ,
,当
 时,
时, ,
, 在
在 上为增函数,
上为增函数,当
 时,
时,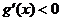 ,
, 在
在 上为减函数,
上为减函数,所以
 时,
时, ,从而
,从而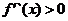 ,所以
,所以 在
在 和
和 上都是增函数.
上都是增函数.由(II)知,
 时,数列
时,数列 单调递增,
单调递增,取
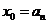 ,因为
,因为 ,所以
,所以
 .
.取
 ,因为
,因为 ,所以
,所以
 .
.所以
 ,即弦
,即弦 的斜率随
的斜率随 单调递增.
单调递增.解法二:设函数
 ,同解法一得,
,同解法一得, 在
在 和
和 上都是增函数,
上都是增函数,所以
 ,
, .
.故
 ,即弦
,即弦 的斜率随
的斜率随 单调递增.
单调递增.湖南文20
设
 是数列
是数列 (
( )的前
)的前 项和,
项和,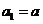 ,且
,且 ,
, ,
,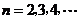 .
.(I)证明:数列
 (
( )是常数数列;
)是常数数列;(II)试找出一个奇数
 ,使以18为首项,7为公比的等比数列
,使以18为首项,7为公比的等比数列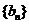 (
( )中的所有项都是数列
)中的所有项都是数列 中的项,并指出
中的项,并指出 是数列
是数列 中的第几项.
中的第几项.