-
(1)“
 ”是“
”是“ ”的( )
”的( )A.充分而不必要条件 B.必要而不充分条件
C.充分不必要条件 D.既不充分也不必要条件
(2)若函数
 ,
,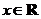 (其中
(其中 ,
, )的最小正周期是
)的最小正周期是 ,且
,且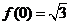 ,则( )
,则( )A.
 B.
B.
C.
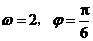 D.
D.
(3)直线
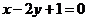 关于直线
关于直线 对称的直线方程是( )
对称的直线方程是( )A.
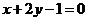 B.
B.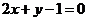
C.
 D.
D.
 (4)要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是关径为6米的圆面,则需安装这种喷水龙头的个数最少是( )
(4)要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是关径为6米的圆面,则需安装这种喷水龙头的个数最少是( )A.
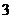 B.
B.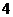 C.
C. D.
D.
(5)已知随机变量
 服从正态分布
服从正态分布 ,
, ,则
,则 ( )
( )A.
 B.
B.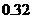 C.
C. D,
D,
(6)若
 两条异面直线
两条异面直线 外的任意一点,则( )
外的任意一点,则( )A.过点
 有且仅有一条直线与
有且仅有一条直线与 都平行
都平行B.过点
 有且仅有一条直线与
有且仅有一条直线与 都垂直
都垂直C.过点
 有且仅有一条直线与
有且仅有一条直线与 都相交
都相交D.过点
 有且仅有一条直线与
有且仅有一条直线与 都异面
都异面(7)若非零向量
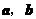 满足
满足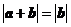 ,则( )
,则( )A.
 B.
B.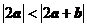
C.
 D.
D. 
(8)设
 是函数
是函数 的导函数,将
的导函数,将 和
和 的图象画在同一个直角坐标系中,不可能正确的是(
)
的图象画在同一个直角坐标系中,不可能正确的是(
)
(9)已知双曲线
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
, 是准线上一点,且
是准线上一点,且 ,
, ,则双曲线的离心率是( )
,则双曲线的离心率是( )A.
 B.
B. C.
C. D.
D.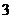
(10)设

 是二次函数,若
是二次函数,若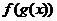 的值域是
的值域是 ,则
,则 的值域是( )
的值域是( )A.
 B.
B.
C.
 D.
D.
第II卷(共100分)
-
(11)已知复数
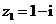 ,
, ,则复数
,则复数 .
.(12)已知
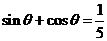 ,且
,且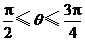 ,则
,则 的值是
.
的值是
.(13)不等式
 的解集是
.
的解集是
.(14)某书店有11种杂志,2元1本的8种,1元1本的3种,小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种数是 (用数字作答).
(15)随机变量
 的分布列如下:
的分布列如下:







其中
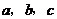 成等差数列,若
成等差数列,若 ,则
,则 的值是 .
的值是 .(16)已知点
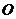 在二面角
在二面角 的棱上,点
的棱上,点 在
在 内,且
内,且 .若对于
.若对于 内异于
内异于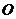 的任意一点
的任意一点 ,都有
,都有 ,则二面角
,则二面角 的大小是 .
的大小是 .(17)设
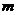 为实数,若
为实数,若 ,则
,则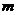 的取值范围是
.
的取值范围是
. -
(18)(本题14分)已知
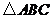 的周长为
的周长为 ,且
,且 .
.(I)求边
 的长;
的长;(II)若
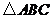 的面积为
的面积为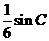 ,求角
,求角 的度数.
的度数.(19)(本题14分)在如图所示的几何体中,
 平面
平面 ,
, 平面
平面 ,
, ,且
,且 ,
, 是
是 的中点.
的中点.(I)求证:
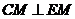 ;
;(II)求
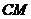 与平面
与平面 所成的角.
所成的角.
 (20)(本题14分)如图,直线
(20)(本题14分)如图,直线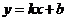 与椭圆
与椭圆 交于
交于 两点,记
两点,记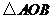 的面积为
的面积为 .
.(I)求在
 ,
, 的条件下,
的条件下, 的最大值;
的最大值;(II)当
 ,
, 时,求直线
时,求直线 的方程.
的方程.(21)(本题15分)已知数列
 中的相邻两项
中的相邻两项 是关于
是关于 的方程
的方程 的两个根,且
的两个根,且 .
.(I)求
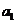 ,
,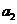 ,
,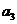 ,
, ;
;(II)求数列
 的前
的前 项和
项和 ;
;(Ⅲ)记
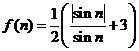 ,
, ,
,求证:
 .
.(22)(本题15分)设
 ,对任意实数
,对任意实数 ,记
,记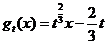 .
.(I)求函数
 的单调区间;
的单调区间;(II)求证:(ⅰ)当
 时,
时,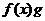
 对任意正实数
对任意正实数 成立;
成立;(ⅱ)有且仅有一个正实数
 ,使得
,使得 对任意正实数
对任意正实数 成立.
成立.
高中毕业班数学全国统一考试试题 数学(理工类) 第I卷(共50分)参考答案
数学(理工类)答案
一、选择题:本题考查基本知识和基本运算.每小题5分,满分50分.
(1)A (2)D (3)D (4)B (5)A
(6)B (7)C (8)D (9)B (10)C
二、填空题:本题考查基本知识和基本运算.每小题4分,满分28分.
(11) (12)
(12) (13)
(13)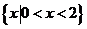 (14)
(14)
(15) (16)
(16)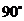 (17)
(17)
三、解答题
(18)解:(I)由题意及正弦定理,得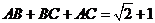 ,
,
 ,
,
两式相减,得 .
.
(II)由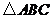 的面积
的面积 ,得
,得 ,
,
由余弦定理,得
 ,
,
所以 .
.
(19)本题主要考查空间线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力和推理运算能力.满分14分.
方法一:
(I)证明:因为 ,
, 是
是 的中点,
的中点,
所以 .
.
又 平面
平面 ,
,
所以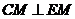 .
.
(II)解:过点 作
作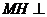 平面
平面 ,垂足是
,垂足是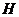 ,连结
,连结 交延长交
交延长交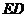 于点
于点 ,连结
,连结 ,
, .
.

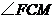 是直线
是直线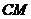 和平面
和平面 所成的角.
所成的角.
因为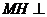 平面
平面 ,
,
所以 ,
,
又因为 平面
平面 ,
,
所以 ,
,
则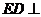 平面
平面 ,因此
,因此 .
.
设 ,
,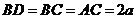 ,
,
在直角梯形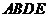 中,
中,
 ,
, 是
是 的中点,
的中点,
所以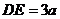 ,
,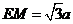 ,
, ,
,
得 是直角三角形,其中
是直角三角形,其中 ,
,
所以 .
.
在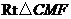 中,
中, ,
,
所以 ,
,
故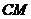 与平面
与平面 所成的角是
所成的角是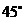 .
.
方法二:
如图,以点 为坐标原点,以
为坐标原点,以 ,
, 分别为
分别为 轴和
轴和 轴,过点
轴,过点 作与平面
作与平面 垂直的直线为
垂直的直线为 轴,建立直角坐标系
轴,建立直角坐标系 ,设
,设 ,则
,则 ,
, ,
, .
. ,
, .
.
(I)证明:因为 ,
,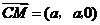 ,
,
所以 ,
,
故 .
.
(II)解:设向量 与平面
与平面 垂直,则
垂直,则 ,
, ,
,
 即
即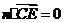 ,
, .
.
因为 ,
, ,
,
所以 ,
,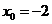 ,
,
即 ,
,
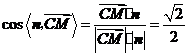 ,
,
直线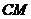 与平面
与平面 所成的角
所成的角 是
是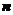 与
与 夹角的余角,
夹角的余角,
所以 ,
,
因此直线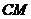 与平面
与平面 所成的角是
所成的角是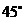 .
.
(20)本题主要考查椭圆的几何性质、椭圆与直线的位置关系等基础知识,考查解析几何的基本思想方法和综合解题能力.满分14分.
(Ⅰ)解:设点 的坐标为
的坐标为 ,点
,点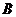 的坐标为
的坐标为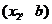 ,
,
由 ,解得
,解得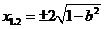 ,
,
所以

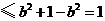 .
.
当且仅当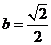 时,
时, 取到最大值
取到最大值 .
.
(Ⅱ)解:由
得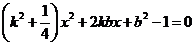 ,
,
 ,
,
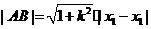
 .
②
.
②
设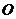 到
到 的距离为
的距离为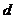 ,则
,则
 ,
,
又因为 ,
,
所以 ,代入②式并整理,得
,代入②式并整理,得
 ,
,
解得 ,
, ,代入①式检验,
,代入①式检验,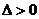 ,
,
故直线 的方程是
的方程是
 或
或 或
或 ,或
,或 .
.
21.本题主要考查等差、等比数列的基本知识,考查运算及推理能力.满分15分.
(I)解:方程 的两个根为
的两个根为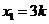 ,
, ,
,
当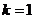 时,
时, ,
,
所以 ;
;
当 时,
时, ,
,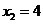 ,
,
所以 ;
;
当 时,
时, ,
, ,
,
所以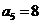 时;
时;
当 时,
时, ,
, ,
,
所以 .
.
(II)解:

 .
.
(III)证明: ,
,
所以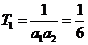 ,
,
 .
.
当 时,
时,
 ,
,
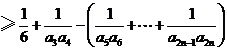
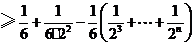
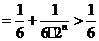 ,
,
同时,

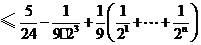
 .
.
综上,当 时,
时, .
.
22.本题主要考查函数的基本性质,导数的应用及不等式的证明等基础知识,以及综合运用所学知识分析和解决问题的能力.满分15分.
(I)解: .
.
由 ,得
,得
 .
.
因为当 时,
时, ,
,
当 时,
时, ,
,
当 时,
时,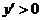 ,
,
故所求函数的单调递增区间是 ,
, ,
,
单调递减区间是 .
.
(II)证明:(i)方法一:
令 ,则
,则
 ,
,
当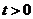 时,由
时,由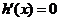 ,得
,得 ,
,
当 时,
时, ,
,
所以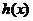 在
在 内的最小值是
内的最小值是 .
.
故当 时,
时, 对任意正实数
对任意正实数 成立.
成立.
方法二:
对任意固定的 ,令
,令 ,则
,则
 ,
,
由 ,得
,得 .
.
当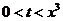 时,
时, .
.
当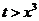 时,
时, ,
,
所以当 时,
时, 取得最大值
取得最大值 .
.
因此当 时,
时, 对任意正实数
对任意正实数 成立.
成立.
(ii)方法一:
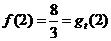 .
.
由(i)得,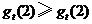 对任意正实数
对任意正实数 成立.
成立.
即存在正实数 ,使得
,使得 对任意正实数
对任意正实数 成立.
成立.
下面证明 的唯一性:
的唯一性:
当 ,
,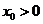 ,
, 时,
时,
 ,
, ,
,
由(i)得, ,
,
再取 ,得
,得 ,
,
所以 ,
,
即 时,不满足
时,不满足 对任意
对任意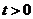 都成立.
都成立.
故有且仅有一个正实数 ,
,
使得 对任意正实数
对任意正实数 成立.
成立.
方法二:对任意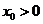 ,
, ,
,
因为 关于
关于 的最大值是
的最大值是 ,所以要使
,所以要使 对任意正实数成立的充分必要条件是:
对任意正实数成立的充分必要条件是:
 ,
,
即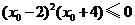 , ①
, ①
又因为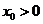 ,不等式①成立的充分必要条件是
,不等式①成立的充分必要条件是 ,
,
所以有且仅有一个正实数 ,
,
使得 对任意正实数
对任意正实数 成立.
成立.