-
22.(本小题满分14分)
设椭圆
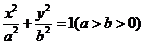 的左、右焦点分别为
的左、右焦点分别为 是椭圆上的一点,
是椭圆上的一点, ,原点
,原点 到直线
到直线 的距离为
的距离为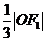 .
.(Ⅰ)证明
 ;
;(Ⅱ)设
 为椭圆上的两个动点,
为椭圆上的两个动点, ,过原点
,过原点 作直线
作直线 的垂线
的垂线 ,垂足为
,垂足为 ,求点
,求点 的轨迹方程.
的轨迹方程. -
22.本小题主要考查椭圆的标准方程和几何性质、直线方程、求曲线的方程等基础知识,考查曲线和方程的关系等解析几何的基本思想方法及推理、运算能力.满分14分.
(Ⅰ)证法一:由题设
 及
及 ,
, ,不妨设点
,不妨设点 ,其中
,其中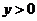 .由于点
.由于点 在椭圆上,有
在椭圆上,有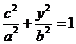 ,即
,即 .
.解得
 ,从而得到
,从而得到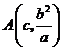 .
.直线
 的方程为
的方程为 ,整理得
,整理得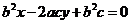 .
.由题设,原点
 到直线
到直线 的距离为
的距离为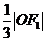 ,即
,即 ,
,将
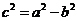 代入上式并化简得
代入上式并化简得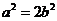 ,即
,即 .
.证法二:同证法一,得到点
 的坐标为
的坐标为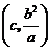 .
.过点
 作
作 ,垂足为
,垂足为 ,易知
,易知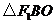

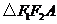 ,故
,故 .
. 由椭圆定义得
由椭圆定义得 ,又
,又 ,
,所以
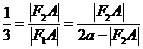 ,
,解得
 ,而
,而 ,得
,得 ,即
,即 .
.(Ⅱ)解法一:设点
 的坐标为
的坐标为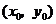 .
.当
 时,由
时,由 知,直线
知,直线 的斜率为
的斜率为 ,所以直线
,所以直线 的方程为
的方程为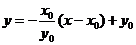 ,或
,或 ,其中
,其中 ,
, .
.点
 的坐标满足方程组
的坐标满足方程组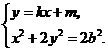
将①式代入②式,得
 ,
,整理得
 ,
,于是
 ,
, .
.由①式得

 .
.由
 知
知 .将③式和④式代入得
.将③式和④式代入得 ,
, .
.将
 代入上式,整理得
代入上式,整理得 .
.当
 时,直线
时,直线 的方程为
的方程为 ,
, 的坐标满足方程组
的坐标满足方程组
所以
 ,
,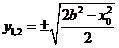 .
.由
 知
知 ,即
,即 ,
,解得
 .
.这时,点
 的坐标仍满足
的坐标仍满足 .
.综上,点
 的轨迹方程为
的轨迹方程为 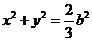 .
.解法二:设点
 的坐标为
的坐标为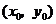 ,直线
,直线 的方程为
的方程为 ,由
,由 ,垂足为
,垂足为 ,可知直线
,可知直线 的方程为
的方程为 .
.记
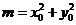 (显然
(显然 ),点
),点 的坐标满足方程组
的坐标满足方程组
由①式得
 . ③
. ③由②式得
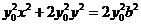 . ④
. ④将③式代入④式得
 .
.整理得
 ,
,于是
 . ⑤
. ⑤由①式得
 . ⑥
. ⑥由②式得
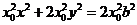 . ⑦
. ⑦将⑥式代入⑦式得
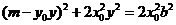 ,
,整理得
 ,
,于是
 . ⑧
. ⑧由
 知
知 .将⑤式和⑧式代入得
.将⑤式和⑧式代入得 ,
, .
.将
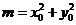 代入上式,得
代入上式,得 .
.所以,点
 的轨迹方程为
的轨迹方程为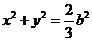 .
.四川文
(5)如果双曲线
 =1上一点P到双曲线右焦点的距离是2,那么点P到y轴的距离是
=1上一点P到双曲线右焦点的距离是2,那么点P到y轴的距离是(A)
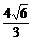 (B)
(B)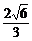 (C)
(C) (D)
(D)
(10)已知抛物线y-x2+3上存在关于直线x+y=0对称的相异两点A、B,则|AB|等于
A.3 B.4 C.3
 D.4
D.4
解析:选C.设直线
 的方程为
的方程为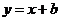 ,由
,由 ,进而可求出
,进而可求出 的中点
的中点 ,又由
,又由 在直线
在直线 上可求出
上可求出 ,∴
,∴ ,由弦长公式可求出
,由弦长公式可求出 .本题考查直线与圆锥曲线的位置关系.自本题起运算量增大.
.本题考查直线与圆锥曲线的位置关系.自本题起运算量增大.(21)(本小题满分12分)
求F1、F2分别是椭圆
 的左、右焦点.
的左、右焦点.(Ⅰ)若r是第一象限内该数轴上的一点,
 ,求点P的作标;
,求点P的作标;(Ⅱ)设过定点M(0,2)的直线l与椭圆交于同的两点A、B,且∠ADB为锐角(其中O为作标原点),求直线
 的斜率
的斜率 的取值范围.
的取值范围.解析:本题主要考查直线、椭圆、平面向量的数量积等基础知识,以及综合运用数学知识解决问题及推理计算能力.
(Ⅰ)易知
 ,
, ,
, .
.∴
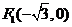 ,
,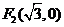 .设
.设
 .则
.则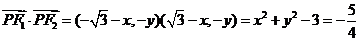 ,又
,又 ,
,联立
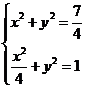 ,解得
,解得 ,
, .
.(Ⅱ)显然
 不满足题设条件.可设
不满足题设条件.可设 的方程为
的方程为 ,设
,设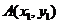 ,
, .
.联立

∴
 ,
,
由

 ,
, ,得
,得 .①
.①又
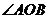 为锐角
为锐角 ,
,∴

又
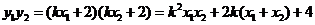
∴

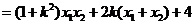
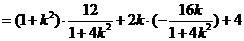


∴
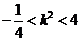 .②
.②综①②可知
 ,∴
,∴ 的取值范围是
的取值范围是 .
.四川理
20)(本小题满分12分)设
 、
、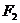 分别是椭圆
分别是椭圆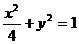 的左、右焦点.
的左、右焦点.(Ⅰ)若
 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求 .
. 的最大值和最小值;
的最大值和最小值;(Ⅱ)设过定点
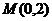 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且∠
,且∠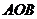 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率 的取值范围.
的取值范围.(20)本题主要考察直线、椭圆、平面向量的数量积等基础知识,以及综合应用数学知识解决问题及推理计算能力。
解:(Ⅰ)解法一:易知

所以
 ,设
,设 ,则
,则
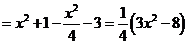
因为
 ,故当
,故当 ,即点
,即点 为椭圆短轴端点时,
为椭圆短轴端点时,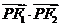 有最小值
有最小值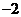
当
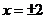 ,即点
,即点 为椭圆长轴端点时,
为椭圆长轴端点时,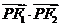 有最大值
有最大值
解法二:易知
 ,所以
,所以 ,设
,设 ,则
,则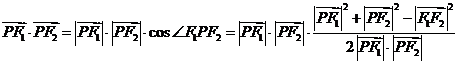
 (以下同解法一)
(以下同解法一)(Ⅱ)显然直线
 不满足题设条件,可设直线
不满足题设条件,可设直线 ,
,联立
 ,消去
,消去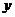 ,整理得:
,整理得:
∴

由
 得:
得: 或
或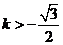
又
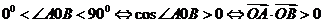
∴

又

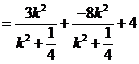
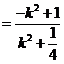
∵
 ,即
,即 ∴
∴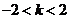
故由①、②得
 或
或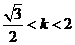
上海理
-
8、已知双曲线
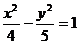 ,则以双曲线中心为焦点,以双曲线左焦点为顶点的抛物线方程为
,则以双曲线中心为焦点,以双曲线左焦点为顶点的抛物线方程为
-
21、已知半椭圆
 与半椭圆
与半椭圆 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中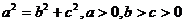 ,
, 是对应的焦点。
是对应的焦点。(1)若三角形
 是边长为1的等边三角形,求“果圆”的方程;
是边长为1的等边三角形,求“果圆”的方程;(2)若
 ,求
,求 的取值范围;
的取值范围;(3)一条直线与果圆交于两点,两点的连线段称为果圆的弦。是否存在实数
 ,使得斜率为
,使得斜率为 的直线交果圆于两点,得到的弦的中点的轨迹方程落在某个椭圆上?若存在,求出所有
的直线交果圆于两点,得到的弦的中点的轨迹方程落在某个椭圆上?若存在,求出所有 的值;若不存在,说明理由。
的值;若不存在,说明理由。 -
21.[解]
(1)∵F0(c,0)F1(0,
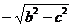 ),F2(0,
),F2(0, )
)∴| F0F1 |=
 ,| F1F2 |=
,| F1F2 |=
于是
 ,
, ,所求“果圆”方程为
,所求“果圆”方程为 (x≥0),
(x≥0),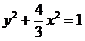 (x≤0). ……4分
(x≤0). ……4分(2)由题意,得a+c>2b,即
 .
.∵(2b)2>b2+c2,∴a2-b2>(2b-a)2,得
 ……7分
……7分又b2>c2=a2-b2,∴
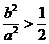 .
.∴
 .
.(3)设“果圆”的方程为
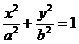 (x≥0)
(x≥0) (x≤0)
(x≤0)记平行弦的斜率为k.
当k=0时,直线y=t(-b≤t≤b)与半椭圆
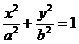 (x≥0)的交点是
(x≥0)的交点是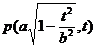 ,与半椭圆
,与半椭圆 (x≤0)的交点是Q(
(x≤0)的交点是Q( ).
).∴P、Q的中点M(x,y)满足

得
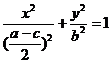 .
.∵a<2b,∴
 .
.综上所述,当k=0时,“果圆”平行弦的中点轨迹总是落在某个椭圆……14分
当k>0时,以k为斜率过B1的直线l与半椭圆
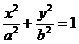 (x≥0)的交点是
(x≥0)的交点是
由此,在直线l右测,以k为斜率的平行弦的中点轨迹在直线
 上,即不在某一椭圆上. ……17分
上,即不在某一椭圆上. ……17分当k<0时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上. ……18分
上海文
-
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分5分,第3小题满分9分.
我们把由半椭圆

 与半椭圆
与半椭圆
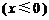 合成的曲线称作“果圆”,其中
合成的曲线称作“果圆”,其中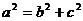 ,
,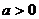 ,
, .
.  如图,设点
如图,设点 ,
, ,
,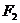 是相应椭圆的焦点,
是相应椭圆的焦点, ,
, 和
和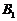 ,
, 是“果圆”
与
是“果圆”
与 ,
, 轴的交点,
轴的交点, 是线段
是线段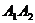 的中点.
的中点.(1)若
 是边长为1的等边三角形,求该
是边长为1的等边三角形,求该“果圆”的方程;
(2)设
 是“果圆”的半椭圆
是“果圆”的半椭圆
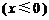 上任意一点.求证:当
上任意一点.求证:当 取得最小值时,
取得最小值时, 在点
在点 或
或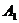 处;
处;(3)若
 是“果圆”上任意一点,求
是“果圆”上任意一点,求 取得最小值时点
取得最小值时点 的横坐标.
的横坐标. -
21.解:(1)

 ,
,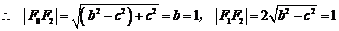 ,
,于是
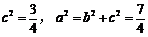 ,
,所求“果圆”方程为
 ,
, .
. (2)设
 ,则
,则
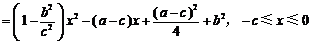 ,
,
 ,
,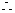
 的最小值只能在
的最小值只能在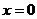 或
或 处取到.
处取到.即当
 取得最小值时,
取得最小值时, 在点
在点 或
或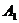 处.
处.
(3)
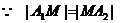 ,且
,且 和
和 同时位于“果圆”的半椭圆
同时位于“果圆”的半椭圆 和半椭圆
和半椭圆 上,所以,由(2)知,只需研究
上,所以,由(2)知,只需研究 位于“果圆”的半椭圆
位于“果圆”的半椭圆 上的情形即可.
上的情形即可.

 .
.当
 ,即
,即 时,
时, 的最小值在
的最小值在 时取到,
时取到,此时
 的横坐标是
的横坐标是 .
.
当
 ,即
,即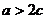 时,由于
时,由于 在
在 时是递减的,
时是递减的, 的最小值在
的最小值在 时取到,此时
时取到,此时 的横坐标是
的横坐标是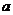 .
.
综上所述,若
 ,当
,当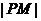 取得最小值时,点
取得最小值时,点 的横坐标是
的横坐标是 ;若
;若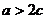 ,当
,当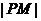 取得最小值时,点
取得最小值时,点 的横坐标是
的横坐标是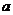 或
或 .
. 陕西文
-
3.抛物线
 的准线方程是
的准线方程是(A)
 (B)
(B)
(C)
 (D)
(D)
-
9.已知双曲线C∶
 >0,b>0),以C的右焦点为圆心且与C的渐近线相切的圆的半径是
>0,b>0),以C的右焦点为圆心且与C的渐近线相切的圆的半径是(A)a (B)b (C)
 (D)
(D)
-
22. (本小题满分14分)
已知椭圆C:
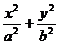 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为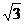 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为
 ,求△AOB面积的最大值.
,求△AOB面积的最大值. -
22.(本小题满分14分)
解:(Ⅰ)设椭圆的半焦距为
 ,依题意
,依题意
 ,
,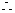 所求椭圆方程为
所求椭圆方程为 .
.(Ⅱ)设
 ,
, .
.(1)当
 轴时,
轴时, .
.(2)当
 与
与 轴不垂直时,
轴不垂直时,设直线
 的方程为
的方程为 .
.由已知
 ,得
,得 .
.把
 代入椭圆方程,整理得
代入椭圆方程,整理得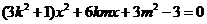 ,
, ,
, .
.
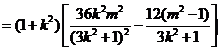
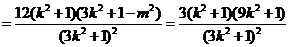
 .
.当且仅当
 ,即
,即 时等号成立.当
时等号成立.当 时,
时, ,
,综上所述
 .
.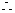 当
当 最大时,
最大时, 面积取最大值
面积取最大值 .
.山东理
(13)设
 是坐标原点,
是坐标原点, 是抛物线
是抛物线 的焦点,
的焦点, 是抛物线上的一点,
是抛物线上的一点,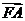 与
与 轴正向的夹角为
轴正向的夹角为 ,则
,则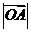 为
.
为
.(21)(本小题满分12分)
已知椭圆
 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为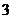 ,最小值为
,最小值为 .
.(Ⅰ)求椭圆
 的标准方程;
的标准方程;(Ⅱ)若直线
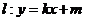 与椭圆
与椭圆 相交于
相交于 ,
, 两点(
两点( 不是左右顶点),且以
不是左右顶点),且以 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求证:直线
的右顶点,求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.[标准答案](I)由题意设椭圆的标准方程为
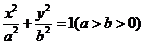
 ,
,
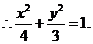
(II)设
 ,由
,由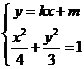 得
得 ,
,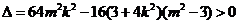 ,
, .
.

 以AB为直径的圆过椭圆的右顶点
以AB为直径的圆过椭圆的右顶点
 ,
, ,
, ,
, ,
, ,解得
,解得 ,且满足
,且满足 .
.当
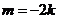 时,
时, ,直线过定点
,直线过定点 与已知矛盾;
与已知矛盾;当
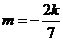 时,
时, ,直线过定点
,直线过定点
综上可知,直线
 过定点,定点坐标为
过定点,定点坐标为
全国2理
-
11.设
 分别是双曲线
分别是双曲线 的左、右焦点,若双曲线上存在点
的左、右焦点,若双曲线上存在点 ,使
,使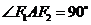 且
且 ,则双曲线的离心率为( )
,则双曲线的离心率为( )A.
 B.
B. C.
C. D.
D.
-
12.设
 为抛物线
为抛物线 的焦点,
的焦点, 为该抛物线上三点,若
为该抛物线上三点,若 ,则
,则 ( )
( )A.9 B.6 C.4 D.3
-
20.(本小题满分12分)
在直角坐标系
 中,以
中,以 为圆心的圆与直线
为圆心的圆与直线 相切.
相切.(1)求圆
 的方程;
的方程;(2)圆
 与
与 轴相交于
轴相交于 两点,圆内的动点
两点,圆内的动点 使
使 成等比数列,求
成等比数列,求 的取值范围.
的取值范围. -
20.解:(1)依题设,圆
 的半径
的半径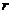 等于原点
等于原点 到直线
到直线 的距离,
的距离,即
 .
.得圆
 的方程为
的方程为 .
.(2)不妨设
 .由
.由 即得
即得 .
.设
 ,由
,由 成等比数列,得
成等比数列,得 ,
,即
 .
.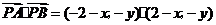
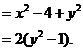
由于点
 在圆
在圆 内,故
内,故
由此得
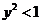 .
.所以
 的取值范围为
的取值范围为 .
.全国2文
-
11.已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率等于( )
A.
 B.
B.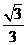 C.
C. D.
D.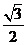
-
12.设
 分别是双曲线
分别是双曲线 的左、右焦点.若点
的左、右焦点.若点 在双曲线上,且
在双曲线上,且 ,则
,则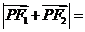 ( )
( )A.
 B.
B.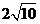 C.
C. D.
D.
全国1理
(4)已知双曲线的离心率为
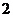 ,焦点是
,焦点是 ,
, ,则双曲线方程为( )
,则双曲线方程为( )A.
 B.
B. C.
C. D.
D.
(11)抛物线
 的焦点为
的焦点为 ,准线为
,准线为 ,经过
,经过 且斜率为
且斜率为 的直线与抛物线在
的直线与抛物线在 轴上方的部分相交于点
轴上方的部分相交于点 ,
,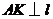 ,垂足为
,垂足为 ,则
,则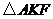 的面积是( )
的面积是( )A.
 B.
B. C.
C. D.
D.
(21)(本小题满分12分)
已知椭圆
 的左、右焦点分别为
的左、右焦点分别为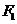 ,
, .过
.过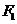 的直线交椭圆于
的直线交椭圆于 两点,过
两点,过 的直线交椭圆于
的直线交椭圆于 两点,且
两点,且 ,垂足为
,垂足为 .
.(Ⅰ)设
 点的坐标为
点的坐标为 ,证明:
,证明: ;
;(Ⅱ)求四边形
 的面积的最小值.
的面积的最小值.(21)证明:
(Ⅰ)椭圆的半焦距
 ,
,由
 知点
知点 在以线段
在以线段 为直径的圆上,故
为直径的圆上,故 ,
,所以,
 .
.(Ⅱ)(ⅰ)当
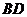 的斜率
的斜率 存在且
存在且 时,
时,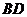 的方程为
的方程为 ,代入椭圆方程
,代入椭圆方程 ,并化简得
,并化简得 .
.设
 ,
, ,则
,则 ,
,
 ;
;因为
 与
与 相交于点
相交于点 ,且
,且 的斜率为
的斜率为 ,
,所以,
 .
.四边形
 的面积
的面积 .
.当
 时,上式取等号.
时,上式取等号.(ⅱ)当
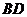 的斜率
的斜率 或斜率不存在时,四边形
或斜率不存在时,四边形 的面积
的面积 .
.综上,四边形
 的面积的最小值为
的面积的最小值为 .
.宁夏理
-
6.已知抛物线
 的焦点为
的焦点为 ,
,点
 ,
, 在抛物线上,
在抛物线上,且
 , 则有( )
, 则有( )A.
 B.
B.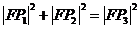
C.
 D.
D.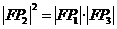
-
13.已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为 .3
-
19.(本小题满分12分)
在平面直角坐标系
 中,经过点
中,经过点 且斜率为
且斜率为 的直线
的直线 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点 和
和 .
.(I)求
 的取值范围;
的取值范围;(II)设椭圆与
 轴正半轴、
轴正半轴、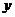 轴正半轴的交点分别为
轴正半轴的交点分别为 ,是否存在常数
,是否存在常数 ,使得向量
,使得向量 与
与 共线?如果存在,求
共线?如果存在,求 值;如果不存在,请说明理由.
值;如果不存在,请说明理由. -
19.解:(Ⅰ)由已知条件,直线
 的方程为
的方程为 ,
,代入椭圆方程得
 .
.整理得
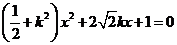 ①
①直线
 与椭圆有两个不同的交点
与椭圆有两个不同的交点 和
和 等价于
等价于 ,
,解得
 或
或 .即
.即 的取值范围为
的取值范围为 .
.(Ⅱ)设
 ,则
,则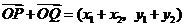 ,
,由方程①,
 . ②
. ②又
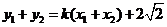 . ③
. ③而
 .
.所以
 与
与 共线等价于
共线等价于 ,
,将②③代入上式,解得
 .
.由(Ⅰ)知
 或
或 ,故没有符合题意的常数
,故没有符合题意的常数 .
.辽宁理
-
11.设
 为双曲线
为双曲线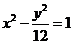 上的一点,
上的一点, 是该双曲线的两个焦点,若
是该双曲线的两个焦点,若 ,则
,则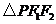 的面积为( )
的面积为( )A.
 B.
B. C.
C. D.
D.
-
14.设椭圆
 上一点
上一点 到左准线的距离为10,
到左准线的距离为10, 是该椭圆的左焦点,若点
是该椭圆的左焦点,若点 满足
满足 ,则
,则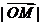 =
.
=
. -
20.(本小题满分14分)
已知正三角形
 的三个顶点都在抛物线
的三个顶点都在抛物线 上,其中
上,其中 为坐标原点,设圆
为坐标原点,设圆 是
是 的内接圆(点
的内接圆(点 为圆心)
为圆心)(I)求圆
 的方程;
的方程;(II)设圆
 的方程为
的方程为 ,过圆
,过圆 上任意一点
上任意一点 分别作圆
分别作圆 的两条切线
的两条切线 ,切点为
,切点为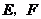 ,求
,求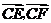 的最大值和最小值.
的最大值和最小值.本小题主要考查平面向量,圆与抛物线的方程及几何性质等基本知识,考查综合运用解析几何知识解决问题的能力.满分14分.
(I)解法一:设
 两点坐标分别为
两点坐标分别为 ,
,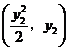 ,由题设知
,由题设知 .
.解得
 ,
,所以
 ,
, 或
或 ,
, .
.设圆心
 的坐标为
的坐标为 ,则
,则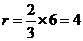 ,所以圆
,所以圆 的方程为
的方程为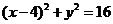 .................................................................................. 4分
.................................................................................. 4分解法二:设
 两点坐标分别为
两点坐标分别为 ,
, ,由题设知
,由题设知 .
.又因为
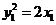 ,
,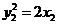 ,可得
,可得 .即
.即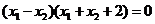 .
.由
 ,
,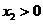 ,可知
,可知 ,故
,故 两点关于
两点关于 轴对称,所以圆心
轴对称,所以圆心 在
在 轴上.
轴上.设
 点的坐标为
点的坐标为 ,则
,则 点坐标为
点坐标为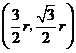 ,于是有
,于是有 ,解得
,解得 ,所以圆
,所以圆 的方程为
的方程为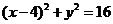 .................................................................................. 4分
.................................................................................. 4分(II)解:设
 ,则
,则 ................................. 8分
................................. 8分在
 中,
中, ,由圆的几何性质得
,由圆的几何性质得
 ,
, ,
,所以
 ,由此可得
,由此可得 .
.则
 的最大值为
的最大值为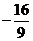 ,最小值为
,最小值为 .
.江西理
-
9.设椭圆
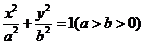 的离心率为
的离心率为 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点 ( )
( )A.必在圆
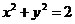 内 B.必在圆
内 B.必在圆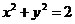 上
上C.必在圆
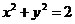 外 D.以上三种情形都有可能
外 D.以上三种情形都有可能 -
21.(本小题满分12分)
 设动点
设动点 到点
到点 和
和 的距离分别为
的距离分别为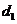 和
和 ,
, ,且存在常数
,且存在常数 ,使得
,使得 .
.(1)证明:动点
 的轨迹
的轨迹 为双曲线,并求出
为双曲线,并求出 的方程;
的方程;(2)过点
 作直线双曲线
作直线双曲线 的右支于
的右支于 两点,试确定
两点,试确定 的范围,使
的范围,使 ,其中点
,其中点 为坐标原点.
为坐标原点.解法一:(1)在
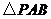 中,
中, ,即
,即 ,
,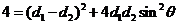 ,即
,即 (常数),
(常数),点
 的轨迹
的轨迹 是以
是以 为焦点,实轴长
为焦点,实轴长 的双曲线.
的双曲线.方程为:
 .
.(2)设
 ,
,
①当
 垂直于
垂直于 轴时,
轴时, 的方程为
的方程为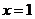 ,
, ,
, 在双曲线上.
在双曲线上.即
 ,因为
,因为 ,所以
,所以 .
.②当
 不垂直于
不垂直于 轴时,设
轴时,设 的方程为
的方程为 .
.由
 得:
得: ,
,由题意知:
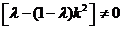 ,
,所以
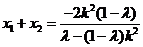 ,
, .
.于是:
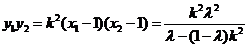 .
.因为
 ,且
,且 在双曲线右支上,所以
在双曲线右支上,所以 .
.由①②知,
 .
.解法二:(1)同解法一
(2)设
 ,
, ,
, 的中点为
的中点为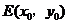 .
.①当
 时,
时,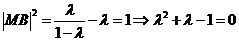 ,
,因为
 ,所以
,所以 ;
;②当
 时,
时, .
.又
 .所以
.所以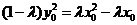 ;
;由
 得
得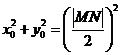 ,由第二定义得
,由第二定义得
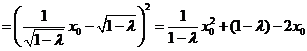 .
.所以
 .
.于是由
 得
得
因为
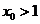 ,所以
,所以 ,又
,又 ,
,解得:
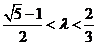 .由①②知
.由①②知 .
.江西文
-
7.连接抛物线
 的焦点
的焦点 与点
与点 所得的线段与抛物线交于点
所得的线段与抛物线交于点 ,设点
,设点 为坐标原点,则三角形
为坐标原点,则三角形 的面积为( )
的面积为( )A.
 B.
B. C.
C. D.
D.
-
12.设椭圆
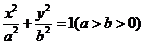 的离心率为
的离心率为 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点 ( )
( )A.必在圆
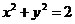 上 B.必在圆
上 B.必在圆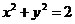 外
外C.必在圆
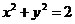 内 D.以上三种情形都有可能
内 D.以上三种情形都有可能 -
22.(本小题满分14分)
设动点
 到点
到点 和
和 的距离分别为
的距离分别为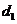 和
和 ,
,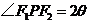 ,且存在常数
,且存在常数 ,使得
,使得 .
. (1)证明:动点
(1)证明:动点 的轨迹
的轨迹 为双曲线,并求出
为双曲线,并求出 的方程;
的方程;(2)如图,过点
 的直线与双曲线
的直线与双曲线 的右支交于
的右支交于 两点.问:是否存在
两点.问:是否存在 ,使
,使 是以点
是以点 为直角顶点的等腰直角三角形?若存在,求出
为直角顶点的等腰直角三角形?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
22.解:(1)在
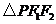 中,
中,


 (小于
(小于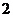 的常数)
的常数)故动点
 的轨迹
的轨迹 是以
是以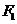 ,
, 为焦点,实轴长
为焦点,实轴长 的双曲线.
的双曲线.方程为
 .
.(2)方法一:在
 中,设
中,设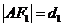 ,
, ,
,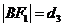 ,
, .
.假设
 为等腰直角三角形,则
为等腰直角三角形,则
由②与③得
 ,
,则
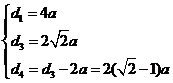
由⑤得
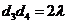 ,
,
 ,
,
故存在
 满足题设条件.
满足题设条件.方法二:(1)设
 为等腰直角三角形,依题设可得
为等腰直角三角形,依题设可得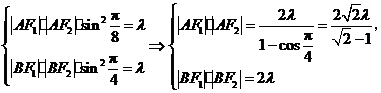
所以
 ,
, .
.则
 .①
.①由
 ,可设
,可设 ,
,则
 ,
, .
.则
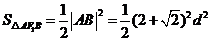 .②
.②由①②得
 .③
.③根据双曲线定义
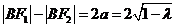 可得,
可得, .
.平方得:
 .④
.④由③④消去
 可解得,
可解得,
故存在
 满足题设条件.
满足题设条件.江苏理
-
3.在平面直角坐标系
 中,双曲线中心在原点,焦点在
中,双曲线中心在原点,焦点在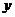 轴上,一条渐近线方程为
轴上,一条渐近线方程为 ,则它的离心率为
,则它的离心率为A.
 B.
B. C.
C. D.
D.
-
15.在平面直角坐标系
 中,已知
中,已知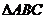 顶点
顶点 和
和 ,顶点
,顶点 在椭圆
在椭圆 上,则
上,则 .
.
-
19、
 (本小题满分14分)如图,在平面直角坐标系
(本小题满分14分)如图,在平面直角坐标系 中,过
中,过 轴正方向上一点
轴正方向上一点 任作一直线,与抛物线
任作一直线,与抛物线 相交于
相交于 两点,一条垂直于
两点,一条垂直于 轴的直线,分别与线段
轴的直线,分别与线段 和直线
和直线 交于
交于 ,
,(1)若
 ,求
,求 的值;(5分)
的值;(5分)(2)若
 为线段
为线段 的中点,求证:
的中点,求证: 为此抛物线的切线;(5分)
为此抛物线的切线;(5分)(3)试问(2)的逆命题是否成立?说明理由。(4分)
解:(1)设过C点的直线为
 ,所以
,所以 ,即
,即 ,设A
,设A ,
,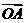 =
= ,
, ,因为
,因为 ,所以
,所以 ,即
,即 ,
,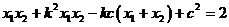
所以
 ,即
,即 所以
所以
(2)设过Q的切线为
 ,
, ,所以
,所以 ,即
,即 ,它与
,它与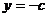 的交点为M
的交点为M ,又
,又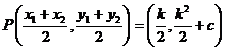 ,所以Q
,所以Q ,因为
,因为 ,所以
,所以 ,所以M
,所以M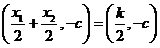 ,所以点M和点Q重合,也就是QA为此抛物线的切线。
,所以点M和点Q重合,也就是QA为此抛物线的切线。(3)(2)的逆命题是成立,由(2)可知Q
 ,因为PQ
,因为PQ
 轴,所以
轴,所以
因为
 ,所以P为AB的中点。
,所以P为AB的中点。 -
9.设
 分别是椭圆
分别是椭圆 (
(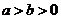 )的左、右焦点,若在其右准线上存在
)的左、右焦点,若在其右准线上存在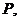 使线段
使线段 的中垂线过点
的中垂线过点 ,则椭圆离心率的取值范围是( )
,则椭圆离心率的取值范围是( )A.
 B.
B. C.
C. D.
D.
-
20.(本小题满分12分)
已知双曲线
 的左、右焦点分别为
的左、右焦点分别为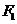 ,
, ,过点
,过点 的动直线与双曲线相交于
的动直线与双曲线相交于 两点.
两点.(I)若动点
 满足
满足 (其中
(其中 为坐标原点),求点
为坐标原点),求点 的轨迹方程;
的轨迹方程;(II)在
 轴上是否存在定点
轴上是否存在定点 ,使
,使 .
. 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
20.解:由条件知
 ,
, ,设
,设 ,
, .
.解法一:(I)设
 ,则
,则 则
则 ,
, ,
,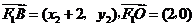 ,由
,由 得
得 即
即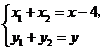
于是
 的中点坐标为
的中点坐标为 .
.当
 不与
不与 轴垂直时,
轴垂直时,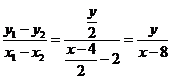 ,即
,即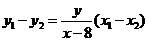 .
.又因为
 两点在双曲线上,所以
两点在双曲线上,所以 ,
, ,两式相减得
,两式相减得 ,即
,即 .
.将
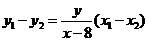 代入上式,化简得
代入上式,化简得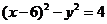 .
.当
 与
与 轴垂直时,
轴垂直时, ,求得
,求得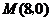 ,也满足上述方程.
,也满足上述方程.所以点
 的轨迹方程是
的轨迹方程是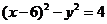 .
.(II)假设在
 轴上存在定点
轴上存在定点 ,使
,使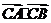 为常数.
为常数.当
 不与
不与 轴垂直时,设直线
轴垂直时,设直线 的方程是
的方程是 .
.代入
 有
有 .
.则
 是上述方程的两个实根,所以
是上述方程的两个实根,所以 ,
, ,
,于是



 .
.因为
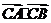 是与
是与 无关的常数,所以
无关的常数,所以 ,即
,即 ,此时
,此时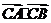 =
= .
.当
 与
与 轴垂直时,点
轴垂直时,点 的坐标可分别设为
的坐标可分别设为 ,
, ,
,此时
 .
.故在
 轴上存在定点
轴上存在定点 ,使
,使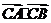 为常数.
为常数.解法二:(I)同解法一的(I)有
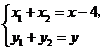
当
 不与
不与 轴垂直时,设直线
轴垂直时,设直线 的方程是
的方程是 .
.代入
 有
有 .
.则
 是上述方程的两个实根,所以
是上述方程的两个实根,所以 .
.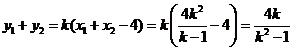 .
. 由①②③得
 .…………………………………………………④
.…………………………………………………④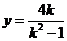 .……………………………………………………………………⑤
.……………………………………………………………………⑤当
 时,
时, ,由④⑤得,
,由④⑤得, ,将其代入⑤有
,将其代入⑤有 .整理得
.整理得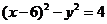 .
.当
 时,点
时,点 的坐标为
的坐标为 ,满足上述方程.
,满足上述方程.当
 与
与 轴垂直时,
轴垂直时, ,求得
,求得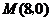 ,也满足上述方程.
,也满足上述方程.故点
 的轨迹方程是
的轨迹方程是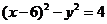 .
.(II)假设在
 轴上存在定点点
轴上存在定点点 ,使
,使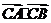 为常数,
为常数,当
 不与
不与 轴垂直时,由(I)有
轴垂直时,由(I)有 ,
, .
.以上同解法一的(II).
湖南文
-
9.设
 分别是椭圆
分别是椭圆 (
(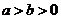 )的左、右焦点,
)的左、右焦点, 是其右准线上纵坐标为
是其右准线上纵坐标为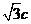 (
( 为半焦距)的点,且
为半焦距)的点,且 ,则椭圆的离心率是( )
,则椭圆的离心率是( )A.
 B.
B. C.
C. D.
D.
-
19.(本小题满分13分)
已知双曲线
 的右焦点为
的右焦点为 ,过点
,过点 的动直线与双曲线相交于
的动直线与双曲线相交于 两点,点
两点,点 的坐标是
的坐标是 .
.(I)证明
 ,
, 为常数;
为常数;(II)若动点
 满足
满足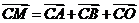 (其中
(其中 为坐标原点),求点
为坐标原点),求点 的轨迹方程.
的轨迹方程. -
19.解:由条件知
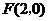 ,设
,设 ,
, .
.(I)当
 与
与 轴垂直时,可设点
轴垂直时,可设点 的坐标分别为
的坐标分别为 ,
, ,
,此时
 .
.当
 不与
不与 轴垂直时,设直线
轴垂直时,设直线 的方程是
的方程是 .
.代入
 ,有
,有 .
.则
 是上述方程的两个实根,所以
是上述方程的两个实根,所以 ,
, ,
,于是
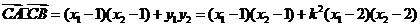
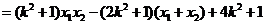

 .
.综上所述,
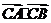 为常数
为常数 .
.(II)解法一:设
 ,则
,则 ,
,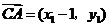 ,
,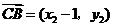 ,
, ,由
,由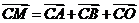 得:
得: 即
即
于是
 的中点坐标为
的中点坐标为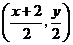 .
.当
 不与
不与 轴垂直时,
轴垂直时, ,即
,即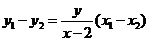 .
.又因为
 两点在双曲线上,所以
两点在双曲线上,所以 ,
, ,两式相减得
,两式相减得 ,即
,即 .
.将
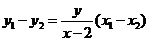 代入上式,化简得
代入上式,化简得 .
.当
 与
与 轴垂直时,
轴垂直时, ,求得
,求得 ,也满足上述方程.
,也满足上述方程.所以点
 的轨迹方程是
的轨迹方程是 .
.解法二:同解法一得
 ……………………………………①
……………………………………①当
 不与
不与 轴垂直时,由(I) 有
轴垂直时,由(I) 有 .…………………②
.…………………②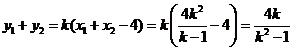 .………………………③
.………………………③由①②③得
 .…………………………………………………④
.…………………………………………………④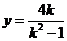 .……………………………………………………………………⑤
.……………………………………………………………………⑤当
 时,
时, ,由④⑤得,
,由④⑤得, ,将其代入⑤有
,将其代入⑤有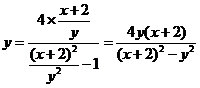 .整理得
.整理得 .
.当
 时,点
时,点 的坐标为
的坐标为 ,满足上述方程.
,满足上述方程.当
 与
与 轴垂直时,
轴垂直时, ,求得
,求得 ,也满足上述方程.
,也满足上述方程.故点
 的轨迹方程是
的轨迹方程是 .
.湖北理
-
7.双曲线
 的左准线为
的左准线为 ,左焦点和右焦点分别为
,左焦点和右焦点分别为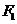 和
和 ;抛物线
;抛物线 的准线为
的准线为 ,焦点为
,焦点为 与
与 的一个交点为
的一个交点为 ,则
,则 等于( )
等于( )A.
 B.
B. C.
C. D.
D.
-
10.已知直线
 (
( 是非零常数)与圆
是非零常数)与圆 有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )
有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )A.60条 B.66条 C.72条 D.78条
-
19.(本小题满分12分)
在平面直角坐标系
 中,过定点
中,过定点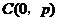 作直线与抛物线
作直线与抛物线 (
( )相交于
)相交于 两点.
两点.(I)若点
 是点
是点 关于坐标原点
关于坐标原点 的对称点,求
的对称点,求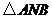 面积的最小值;
面积的最小值;(II)是否存在垂直于
 轴的直线
轴的直线 ,使得
,使得 被以
被以 为直径的圆截得的弦长恒为定值?若存在,求出
为直径的圆截得的弦长恒为定值?若存在,求出 的方程;若不存在,说明理由.(此题不要求在答题卡上画图)
的方程;若不存在,说明理由.(此题不要求在答题卡上画图)
-
19.本小题主要考查直线、圆和抛物线等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力.
解法1:(Ⅰ)依题意,点
 的坐标为
的坐标为 ,可设
,可设 ,
,直线
 的方程为
的方程为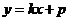 ,与
,与 联立得
联立得 消去
消去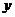 得
得 .
. 由韦达定理得
由韦达定理得 ,
, .
.于是
 .
.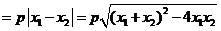
 ,
, 当
当 时,
时, .
.(Ⅱ)假设满足条件的直线
 存在,其方程为
存在,其方程为 ,
, 的中点为
的中点为 ,
, 与
与 为直径的圆相交于点
为直径的圆相交于点 ,
, 的中点为
的中点为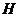 ,
, 则
则 ,
, 点的坐标为
点的坐标为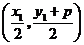 .
. ,
, ,
,
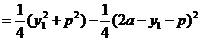
 ,
,
 .
.令
 ,得
,得 ,此时
,此时 为定值,故满足条件的直线
为定值,故满足条件的直线 存在,其方程为
存在,其方程为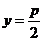 ,
,即抛物线的通径所在的直线.
解法2:(Ⅰ)前同解法1,再由弦长公式得
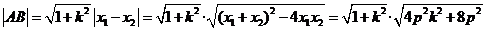
 ,
,又由点到直线的距离公式得
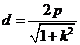 .
.从而
 ,
, 当
当 时,
时, .
.(Ⅱ)假设满足条件的直线
 存在,其方程为
存在,其方程为 ,则以
,则以 为直径的圆的方程为
为直径的圆的方程为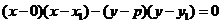 ,
,将直线方程
 代入得
代入得 ,
,则
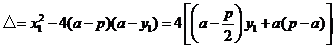 .
.设直线
 与以
与以 为直径的圆的交点为
为直径的圆的交点为 ,
,则有
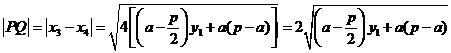 .
.令
 ,得
,得 ,此时
,此时 为定值,故满足条件的直线
为定值,故满足条件的直线 存在,其方程为
存在,其方程为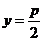 ,
,即抛物线的通径所在的直线.
湖北文
-
12.过双曲线
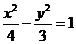 左焦点
左焦点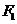 的直线交曲线的左支于
的直线交曲线的左支于 两点,
两点, 为其右焦点,则
为其右焦点,则 的值为______.
的值为______.广东理
-
11.在平面直角坐标系
 中,有一定点
中,有一定点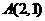 ,若线段
,若线段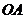 的垂直平分线过抛物线
的垂直平分线过抛物线 则该抛物线的方程是
.
则该抛物线的方程是
. -
18. (本小题满分14分)
在平面直角坐标系
 中,已知圆心在第二象限、半径为
中,已知圆心在第二象限、半径为 的圆
的圆 与直线
与直线 相切于
相切于坐标原点
 .椭圆
.椭圆 与圆
与圆 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为 .
.(1)求圆
 的方程;
的方程;(2)试探究圆
 上是否存在异于原点的点
上是否存在异于原点的点 ,使
,使 到椭圆右焦点
到椭圆右焦点 的距离等于线段
的距离等于线段 的长.若存在,请求出点
的长.若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
18. 解: (1)设圆心坐标为(m,n)(m<0,n>0),则该圆的方程为(x-m)2+(y-n)2=8已知该圆与直线y=x相切,那么圆心到该直线的距离等于圆的半径,则
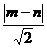 =2
=2
即
 =4
①
=4
① 又圆与直线切于原点,将点(0,0)代入得
m2+n2=8 ②
联立方程①和②组成方程组解得
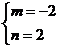

 故圆的方程为(x+2)2+(y-2)2=8
故圆的方程为(x+2)2+(y-2)2=8(2)
 =5,∴a2=25,则椭圆的方程为 + =1
=5,∴a2=25,则椭圆的方程为 + =1其焦距c=
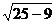 =4,右焦点为(4,0),那么
=4,右焦点为(4,0),那么 =4。
=4。要探求是否存在异于原点的点Q,使得该点到右焦点F的距离等于
 的长度4,我们可以转化为探求以右焦点F为顶点,半径为4的圆(x─4)2+y2=8与(1)所求的圆的交点数。
的长度4,我们可以转化为探求以右焦点F为顶点,半径为4的圆(x─4)2+y2=8与(1)所求的圆的交点数。通过联立两圆的方程解得x=
 ,y=
,y=
即存在异于原点的点Q(
 ,
, ),使得该点到右焦点F的距离等于
),使得该点到右焦点F的距离等于 的长。
的长。广东文
-
11.在平面直角坐标系
 中,已知抛物线关于
中,已知抛物线关于 轴对称,顶点在原点
轴对称,顶点在原点 ,且过点P(2,4),则该抛物线的方程是
.
,且过点P(2,4),则该抛物线的方程是
.
19(本小题满分14分)
在平面直角坐标系
 中,已知圆心在第二象限、半径为2/2的圆
中,已知圆心在第二象限、半径为2/2的圆 与直线
与直线 相切于
相切于坐标原点
 .椭圆
.椭圆 与圆
与圆 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为 .
.(1)求圆
 的方程;
的方程;(2)试探究圆
 上是否存在异于原点的点
上是否存在异于原点的点 ,使
,使 到椭圆右焦点F的距离等于线段
到椭圆右焦点F的距离等于线段 的长.若存在,请求出点
的长.若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.19解:(1) 设圆C 的圆心为 (m, n)
则
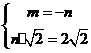 解得
解得
所求的圆的方程为

(2) 由已知可得


椭圆的方程为
 , 右焦点为 F( 4, 0) ;
, 右焦点为 F( 4, 0) ;假设存在Q点
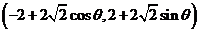 使
使 ,
,
整理得
 代入
代入  得:
得: ,
, 
因此不存在符合题意的Q点.
福建理
-
6.以双曲线
 的右焦点为圆心,且与其渐近线相切的圆的方程是( )
的右焦点为圆心,且与其渐近线相切的圆的方程是( )A.
 B.
B.
C.
 D.
D.
-
20.
 (本小题满分12分)如图,已知点
(本小题满分12分)如图,已知点 ,
,直线
 ,
, 为平面上的动点,过
为平面上的动点,过 作直线
作直线 的垂线,垂足为点
的垂线,垂足为点 ,且
,且 .
.(Ⅰ)求动点
 的轨迹
的轨迹 的方程;
的方程;(Ⅱ)过点
 的直线交轨迹
的直线交轨迹 于
于 两点,交直线
两点,交直线 于点
于点 ,已知
,已知 ,
, ,求
,求 的值;
的值; -
20.本小题主要考查直线、抛物线、向量等基础知识,考查轨迹方程的求法以及研究曲线几何特征的基本方法,考查运算能力和综合解题能力.满分14分.
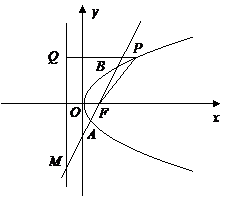 解法一:(Ⅰ)设点
解法一:(Ⅰ)设点 ,则
,则 ,由
,由 得:
得: ,化简得
,化简得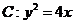 .
.(Ⅱ)设直线
 的方程为:
的方程为: .
.设
 ,
, ,又
,又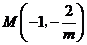 ,
,联立方程组
 ,消去
,消去 得:
得: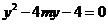 ,
, ,故
,故
由
 ,
, 得:
得: ,
, ,整理得:
,整理得: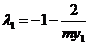 ,
, ,
,


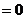 .
.解法二:(Ⅰ)由
 得:
得: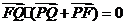 ,
,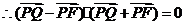 ,
, ,
, .
.所以点
 的轨迹
的轨迹 是抛物线,由题意,轨迹
是抛物线,由题意,轨迹 的方程为:
的方程为: .
.(Ⅱ)由已知
 ,
, ,得
,得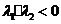 .
.则:
 .…………①
.…………①过点
 分别作准线
分别作准线 的垂线,垂足分别为
的垂线,垂足分别为 ,
, ,
,则有:
 .…………②
.…………②由①②得:
 ,即
,即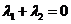 .
.福建文
-
10.以双曲线
 的右焦点为圆心,且与其右准线相切的圆的方程是( )
的右焦点为圆心,且与其右准线相切的圆的方程是( )A.
 B.
B.
C.
 D.
D.
-
22.(本小题满分14分)
如图,已知
 ,直线
,直线 ,
, 为平面上的动点,过点
为平面上的动点,过点 作
作 的垂线,垂足为点
的垂线,垂足为点 ,且
,且 .
.(Ⅰ)求动点
 的轨迹
的轨迹 的方程;
的方程;(Ⅱ)过点
 的直线交轨迹
的直线交轨迹 于
于 两点,交直线
两点,交直线 于点
于点 .
.(1)已知
 ,
, ,求
,求 的值;
的值;(2)求
 的最小值.
的最小值. -
22.本小题主要考查直线、抛物线、向量等基础知识,考查轨迹方程的求法以及研究曲线几何特征的基本方法,考查运算能力和综合解题能力.满分14分.
 解法一:(Ⅰ)设点
解法一:(Ⅰ)设点 ,则
,则 ,由
,由 得:
得: ,化简得
,化简得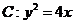 .
.(Ⅱ)(1)设直线
 的方程为:
的方程为: .
.设
 ,
, ,又
,又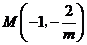 ,
,联立方程组
 ,消去
,消去 得:
得: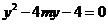 ,
, ,
,
由
 ,
, 得:
得: ,
, ,整理得:
,整理得: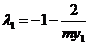 ,
, ,
,


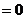 .
.解法二:(Ⅰ)由
 得:
得: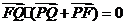 ,
,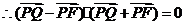 ,
, ,
, .
.所以点
 的轨迹
的轨迹 是抛物线,由题意,轨迹
是抛物线,由题意,轨迹 的方程为:
的方程为: .
.(Ⅱ)(1)由已知
 ,
, ,得
,得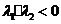 .
.则:
 .…………①
.…………①过点
 分别作准线
分别作准线 的垂线,垂足分别为
的垂线,垂足分别为 ,
, ,
,则有:
 .…………②
.…………②由①②得:
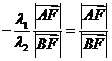 ,即
,即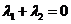 .
.(Ⅱ)(2)解:由解法一,

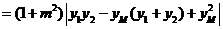

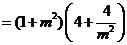
 .
.当且仅当
 ,即
,即 时等号成立,所以
时等号成立,所以 最小值为
最小值为 .
.北京理
-
17.(本小题共14分)
矩形
 的两条对角线相交于点
的两条对角线相交于点 ,
, 边所在直线的方程为
边所在直线的方程为 ,点
,点 在
在 边所在直线上.
边所在直线上.(I)求
 边所在直线的方程;
边所在直线的方程;(II)求矩形
 外接圆的方程;
外接圆的方程;(III)若动圆
 过点
过点 ,且与矩形
,且与矩形 的外接圆外切,求动圆
的外接圆外切,求动圆 的圆心的轨迹方程.
的圆心的轨迹方程. -
17.(共14分)
解:(I)因为
 边所在直线的方程为
边所在直线的方程为 ,且
,且 与
与 垂直,所以直线
垂直,所以直线 的斜率为
的斜率为 .
.又因为点
 在直线
在直线 上,
上,所以
 边所在直线的方程为
边所在直线的方程为 .
. .
.(II)由
 解得点
解得点 的坐标为
的坐标为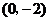 ,
,因为矩形
 两条对角线的交点为
两条对角线的交点为 .
.所以
 为矩形
为矩形 外接圆的圆心.
外接圆的圆心.又
 .
.从而矩形
 外接圆的方程为
外接圆的方程为 .
.(III)因为动圆
 过点
过点 ,所以
,所以 是该圆的半径,又因为动圆
是该圆的半径,又因为动圆 与圆
与圆 外切,
外切,所以
 ,
,即
 .
.故点
 的轨迹是以
的轨迹是以 为焦点,实轴长为
为焦点,实轴长为 的双曲线的左支.
的双曲线的左支.因为实半轴长
 ,半焦距
,半焦距 .
.所以虚半轴长
 .
.从而动圆
 的圆心的轨迹方程为
的圆心的轨迹方程为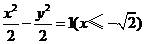 .
.北京文
-
4.椭圆
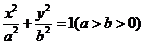 的焦点为
的焦点为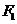 ,
, ,两条准线与
,两条准线与 轴的交点分别为
轴的交点分别为 ,若
,若 ,则该椭圆离心率的取值范围是( )
,则该椭圆离心率的取值范围是( )A.
 B.
B. C.
C. D.
D.
-
19.(本小题共14分)
 如图,矩形
如图,矩形 的两条对角线相交于点
的两条对角线相交于点 ,
, 边所在直线的方程为
边所在直线的方程为 点
点 在
在 边所在直线上.
边所在直线上.(I)求
 边所在直线的方程;
边所在直线的方程;(II)求矩形
 外接圆的方程;
外接圆的方程;(III)若动圆
 过点
过点 ,且与矩形
,且与矩形 的外接圆外切,求动圆
的外接圆外切,求动圆 的圆心的轨迹方程.
的圆心的轨迹方程. -
19.(共14分)
解:(I)因为
 边所在直线的方程为
边所在直线的方程为 ,且
,且 与
与 垂直,所以直线
垂直,所以直线 的斜率为
的斜率为 .
.又因为点
 在直线
在直线 上,
上,所以
 边所在直线的方程为
边所在直线的方程为 .
. .
.(II)由
 解得点
解得点 的坐标为
的坐标为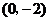 ,
,因为矩形
 两条对角线的交点为
两条对角线的交点为 .
.所以
 为矩形
为矩形 外接圆的圆心.
外接圆的圆心.又
 .
.从而矩形
 外接圆的方程为
外接圆的方程为 .
.(III)因为动圆
 过点
过点 ,所以
,所以 是该圆的半径,又因为动圆
是该圆的半径,又因为动圆 与圆
与圆 外切,
外切,所以
 ,
,即
 .
.故点
 的轨迹是以
的轨迹是以 为焦点,实轴长为
为焦点,实轴长为 的双曲线的左支.
的双曲线的左支.因为实半轴长
 ,半焦距
,半焦距 .
.所以虚半轴长
 .
.从而动圆
 的圆心的轨迹方程为
的圆心的轨迹方程为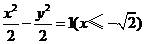 .
.安徽理
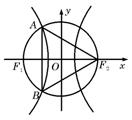 (9)如图,
(9)如图, 和
和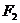 分别是双曲线
分别是双曲线 的两个焦点,
的两个焦点, 和
和 是以
是以 为圆心,以
为圆心,以 为半径的圆与该双曲线左支的两个交点,且△
为半径的圆与该双曲线左支的两个交点,且△ 是等边三角形,则双曲线的离心率为
是等边三角形,则双曲线的离心率为(A)
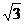 (B)
(B)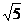 (C)
(C) (D)
(D)
 (14)如图,抛物线y=-x2+1与x轴的正半轴交于点A,将线段OA的n等分点从左至右依次记为P1,P2,…,Pn-1,过这些分点分别作x轴的垂线,与抛物线的交点依次为Q1,Q2,…,Qn-1,从而得到n-1个直角三角形△Q1OP1, △Q2P1P2,…, △Qn-1Pn-1Pn-1,当n→∞时,这些三角形的面积之和的极限为
.
(14)如图,抛物线y=-x2+1与x轴的正半轴交于点A,将线段OA的n等分点从左至右依次记为P1,P2,…,Pn-1,过这些分点分别作x轴的垂线,与抛物线的交点依次为Q1,Q2,…,Qn-1,从而得到n-1个直角三角形△Q1OP1, △Q2P1P2,…, △Qn-1Pn-1Pn-1,当n→∞时,这些三角形的面积之和的极限为
. 
(19) (本小题满分12分)
如图,曲线G的方程为y2=2x(y≥0).以原点为圆心,以t(t >0)为半径的圆分别与曲线G和y轴的正半轴相交于点A与点B.直线AB与x轴相交于点C.
(Ⅰ)求点A的横坐标a与点C的横坐标c的关系式;
(Ⅱ)设曲线G上点D的横坐标为a+2,求证:
直线CD的斜率为定值.
-
19.本小题综合考查平面解析几何知识,主要涉及平面直角坐标系中的两点间距离公式、直线的方程与斜率、抛物线上的点与曲线方程的关系,考查运算能力与思维能力、综合分析问题的能力.本小题满分12分.
 解:(Ⅰ)由题意知,
解:(Ⅰ)由题意知, .
.因为
 ,所以
,所以 .
.由于
 ,故有
,故有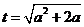 . (1)
. (1)由点
 的坐标知,
的坐标知,直线
 的方程为
的方程为 .
.又因点
 在直线
在直线 上,故有
上,故有 ,
,将(1)代入上式,得
 ,
,解得
 .
.(Ⅱ)因为
 ,所以直线
,所以直线 的斜率为
的斜率为 .
.所以直线
 的斜率为定值.
的斜率为定值.安徽文
(2)椭圆
 的离心率为
的离心率为(A)
 (B)
(B) (C)
(C) (D)
(D)
(18)(本小题满分14分)
设F是抛物线G:x2=4y的焦点.
(Ⅰ)过点P(0,-4)作抛物线G的切线,求切线方程:
(Ⅱ)设A、B为势物线G上异于原点的两点,且满足
 ,延长AF、BF分别交抛物线G于点C,D,求四边形ABCD面积的最小值.
,延长AF、BF分别交抛物线G于点C,D,求四边形ABCD面积的最小值. -
18.本小题主要考查抛物线的方程与性质,抛物线的切点与焦点,向量的数量积,直线与抛物线的位置关系,平均不等式等基础知识,考查综合分析问题、解决问题的能力.本小题满分14分.
解:(I)设切点
 .由
.由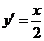 ,知抛物线在
,知抛物线在 点处的切线斜率为
点处的切线斜率为 ,故所求切线方程为
,故所求切线方程为 .
.即
 .
.因为点
 在切线上.
在切线上.所以
 ,
, ,
, .
.所求切线方程为
 .
.(II)设
 ,
, .
.由题意知,直线
 的斜率
的斜率 存在,由对称性,不妨设
存在,由对称性,不妨设 .
.因直线
 过焦点
过焦点 ,所以直线
,所以直线 的方程为
的方程为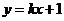 .
.点
 的坐标满足方程组
的坐标满足方程组
得
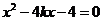 ,
,由根与系数的关系知
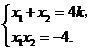
 .
.因为
 ,所以
,所以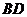 的斜率为
的斜率为 ,从而
,从而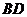 的方程为
的方程为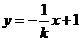 .
.同理可求得
 .
.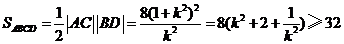 .
.当
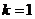 时,等号成立.所以,四边形
时,等号成立.所以,四边形 面积的最小值为
面积的最小值为 .
.