-
1. 若集合
 ,
, ,则“
,则“ ”是“
”是“ ”的 (
A )
”的 (
A )A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
-
2.
 ,且
,且 ,则向量
,则向量 与
与 的夹角为
( C )
的夹角为
( C )A.
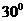 B.
B. C.
C. D.
D.
-
3. 一个与球心距离为
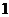 的平面截球所得圆的面积为
的平面截球所得圆的面积为 ,则球的表面积为 (
B )
,则球的表面积为 (
B )A.
 B.
B. C.
C. D.
D.
-
4. 设变量
 ,
,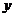 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最小值为 (
B )
的最小值为 (
B )A.
 B.
B. C.
C.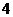 D.
D.
-
5. 已知△ABC的周长为9,且
 ,则cosC的值为 ( A )
,则cosC的值为 ( A )A.
 B.
B. C.
C. D.
D.
-
6. 已知直线
 是函数
是函数 图象的一条对称轴,则函数
图象的一条对称轴,则函数 图象的一条对称轴方程是 ( B )
图象的一条对称轴方程是 ( B )A.
 B.
B. C.
C. D.
D.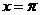
-
7.若
 的方差为3,则
的方差为3,则 的标准差为 ( B )
的标准差为 ( B )A.12 B.
 C.16
D.4
C.16
D.4 8
3
4
1
5
9
6
7
2
-
8. 将
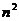 个正整数
个正整数 填入
填入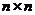 方格中,使其每行、每列、每条对角线上的数的和都相等,这个正方形叫做
方格中,使其每行、每列、每条对角线上的数的和都相等,这个正方形叫做 阶幻方.记
阶幻方.记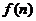 为
为 阶幻方对角线上数的和,如右图就是一个
阶幻方对角线上数的和,如右图就是一个 阶幻方,可知
阶幻方,可知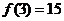 .已知将等差数列:
.已知将等差数列: 前
前 项填入
项填入 方格中,可得到一个
方格中,可得到一个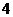 阶幻方,则其对角线上数的和等于
( C )
阶幻方,则其对角线上数的和等于
( C )A.
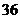 B.
B. C.
C. D.
D.
-
必做题: 以下四题为必做题.
9.程序框图(如图)的运算结果为 。
-
10.
 展开式中的常数项是 。
展开式中的常数项是 。 -
11. 定义在R上的偶函数

 的x的范围为 。
的x的范围为 。 -
12. 以下四个关于圆锥曲线的命题中
①过圆内一点(非圆心)作圆的动弦
 ,则
,则 中点的轨迹为椭圆;
中点的轨迹为椭圆;②设
 、
、 为两个定点,若
为两个定点,若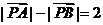 ,则动点
,则动点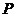 的轨迹为双曲线的一支;
的轨迹为双曲线的一支;③方程
 的两个根可分别作为椭圆和双曲线的离心率;
的两个根可分别作为椭圆和双曲线的离心率;④无论方程
 表示的是椭圆还是双曲线,它们都有相同的焦点。
表示的是椭圆还是双曲线,它们都有相同的焦点。其中真命题的序号为 . (写出所有真命题的序号).
选做题: 从以下三题中选做两题,如三题都做,按前两题的得分记分.
-
13.自极点O向直线l作垂线,垂足是H(
 ),则直线l的极坐标方程为 。
),则直线l的极坐标方程为 。 -
14. 若不等式|x-2|+|x+3|<
 的解集为Æ,则
的解集为Æ,则 的取值范围为_____________。
的取值范围为_____________。
-
15. 如图,⊙O和⊙
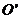 都经过A、B两点,AC是⊙
都经过A、B两点,AC是⊙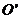
的切线,交⊙O于点C,AD是⊙O的切线,交⊙
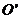 于
于点D,若BC= 2,BD=6,则AB的长为 。
-
16.(本小题满分12分)
已知
 ,且
,且 对任意实数x恒成立.
对任意实数x恒成立.(Ⅰ)求
 的值;
的值;
(Ⅱ)求函数82615980
 的单调增区间.
的单调增区间.
-
17.(本小题满分12分)
有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一组成.
第一排
明文字符
A
B
C
D
密码字符
11
12
13
14
第二排
明文字符
E
F
G
H
密码字符
21
22
23
24
第三排
明文字符
M
N
P
Q
密码字符
1
2
3
4
设随机变量ξ表示密码中不同数字的个数.
(Ⅰ)求P(ξ=2)
(Ⅱ)求随机变量ξ的分布列和它的数学期望.
-
18.(本题满分14分)
如图:
 平面
平面 ,四边形
,四边形 是矩形,
是矩形, ,
, 与平面
与平面 所成的角是
所成的角是 ,点
,点 是
是 的中点,点
的中点,点 在边
在边 上移动.
上移动. (1)当点
(1)当点 为
为 的中点时,试判断
的中点时,试判断 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由;(2)证明:不论点
 在边
在边 上何处,都有
上何处,都有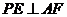 ;
;(3)
 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为 .
. -
19.(本小题满分14分)
设函数f(x)=x3+ax2+bx+c在x=1处取得极值-2,试用c表示a和b,并求f(x)的单调区间。
-
20.(本小题满分14分)
 如图,已知直线l与半径为1的⊙D相切于点C,动点P到直线l的距离为d,若
如图,已知直线l与半径为1的⊙D相切于点C,动点P到直线l的距离为d,若
(Ⅰ)求点P的轨迹方程;
(Ⅱ)若轨迹上的点P与同一平面上的点G、M分别满足
 ,
,求以P、G、D为项点的三角形的面积.
-
21.(本小题满分14分)
设无穷数列{an}具有以下性质:①a1=1;②当

(Ⅰ)请给出一个具有这种性质的无穷数列,使得不等式
 对于任意的
对于任意的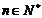 都成立,并对你给出的结果进行验证(或证明);
都成立,并对你给出的结果进行验证(或证明);(Ⅱ)若
 ,其中
,其中 ,且记数列{bn}的前n项和Bn,证明:
,且记数列{bn}的前n项和Bn,证明:
高考理科数学模拟试题( 理 科 2 )参考答案
数 学 试 题 ( 理 科 2 )参考答案
一.选择题 A C B B A B B C
二.填空题  ;
;
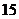 ;
;
 ; ③④;
; ③④;  ;
;  ;
;  。
。
三.解答题
16.解:(Ⅰ)
 ……………2分
……………2分
由题意知 对任意实数x恒成立,
对任意实数x恒成立,
得 ,
,
 ………………………………………………………6分
………………………………………………………6分
(Ⅱ)由(Ⅰ)知
由 ,解得
,解得
所以, 的单调增区间为
的单调增区间为 ……………………12分
……………………12分
17.解:(Ⅰ)密码中不同数字的个数为2的事件为密码中只有两个数字,注意到密码的第1,2列分别总是1,2,即只能取表格第1,2列中的数字作为密码.
 …………………………………………………………………4分
…………………………………………………………………4分
(Ⅱ)由题意可知,ξ的取值为2,3,4三种情形.
若ξ=
3,注意表格的第一排总含有数字1,第二排总含有数字2则密码中只可能取数字1,2,3或1,2,4.

若
(或用 求得). ………………………………………………8分
求得). ………………………………………………8分
 的分布列为:
的分布列为:
|
ξ |
2 |
3 |
4 |
|
p |
 |
 |
 |
 ………………………………………………12分
………………………………………………12分
18.证明:(1)当点 为
为 的中点时,
的中点时, 与平面
与平面 平行.
平行.
∵在 中,
中, 、
、 分别为
分别为 、
、 的中点
的中点
∴ ∥
∥ 又
又 平面
平面 ,而
,而 平面
平面
∴ ∥平面
∥平面 .
……………………4分
.
……………………4分
(2)证明(略证):易证 平面
平面 ,又
,又 是
是 在平面
在平面 内的射影,
内的射影,
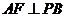 ,∴
,∴ .
……………………8分
.
……………………8分
(3)∵ 与平面
与平面 所成的角是
所成的角是 ,∴
,∴ ,
, ,
, .
.
 过
过 作
作 于
于 ,连
,连 ,则
,则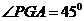 .
…………………10分
.
…………………10分
易知: ,
, ,设
,设 ,则
,则 ,
, ,
,
在 中,
中,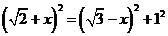 ,
,
得 .
………14分
.
………14分
解法二:(向量法)(1)同解法一
 (2)建立图示空间直角坐标系,则
(2)建立图示空间直角坐标系,则 ,
,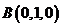 ,
, ,
,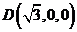 .
.
设 ,则
,则 ,
,
∴ (本小题4分)
(本小题4分)
(3)设平面 的法向量为
的法向量为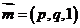 ,由
,由 ,
,
得: ,依题意
,依题意 ,
,
∴ ,得
,得 .
(本小题6分)
.
(本小题6分)
19.解:依题意有 而
而

故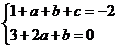 得
得 从而
从而 。
。
令 ,得
,得 或
或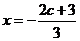 。
。
由于 在
在 处取得极值,故
处取得极值,故 ,即
,即 。
。
(1) 若 ,即
,即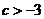 ,则当
,则当 时,
时, ;
;
当 时,
时, ;当
;当 时,
时, ;
;
从而 的单调增区间为
的单调增区间为 ;单调减区间为
;单调减区间为
(2) 若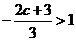 ,即
,即 ,同上可得,
,同上可得,
 的单调增区间为
的单调增区间为 ;单调减区间为
;单调减区间为
20.解:(Ⅰ)
∴点P的轨迹是D为焦点,l为相应准线的椭圆.
由
以CD所在直线为x轴,以CD与⊙D的另一个交点O为坐标原点建立直角坐标系.
∴所求点P的轨迹方程为 ………………………………………………6分
………………………………………………6分
(说明:其它建系方式相应给分)
(Ⅱ) G为椭圆的左焦点.
G为椭圆的左焦点.
又
由题意,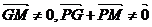 (否则P、G、M、D四点共线与已经矛盾)
(否则P、G、M、D四点共线与已经矛盾)

又∵点P在椭圆上, 
又
 ……………………………………………………14分
……………………………………………………14分
21.解:(Ⅰ)令 ,
,
则无穷数列{an}可由a1 = 1, 给出.
给出.
显然,该数列满足 ,且
,且
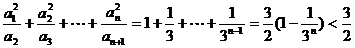 ……………………6分
……………………6分
(Ⅱ)
 ………………………………………………8分
………………………………………………8分
又



 …………………………………………………………………14分
…………………………………………………………………14分